In this experiment you will use a diffraction-grating spectrometer to measure the wavelengths of the emission lines of hydrogen. With these measured wavelengths you will compute the Rydberg constant. To perform this experiment intelligently, you need to understand two things: (1) how a diffraction grating works and (2) the Bohr model of the hydrogen atom.

Diffraction grating. A diffraction grating is simply a piece of glass or plastic which has a series of very fine scratches or grooves cut in its surface. The grooves are perfectly straight and parallel and are equally spaced so that there are a fixed number of grooves per millimeter, typically around 500 grooves/mm.

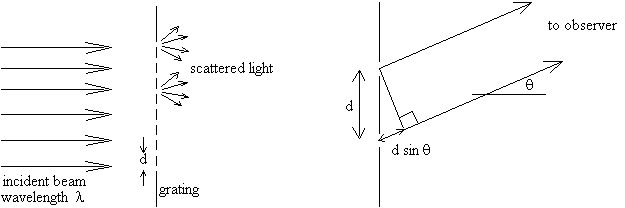
A grating behaves essentially like a multi-slit aperture, that is, a mask with many closely spaced slits. If the number of grooves per length is n (grooves per cm), then the separation between adjacent slits is d = 1/n (cm per line or simply, cm). Consider what happens when a beam of monochromatic (single wavelength) light strikes a grating at normal incidence, as shown below. Each groove or slit scatters the light in all forward directions. However, in only certain directions will the light scattered from different grooves interfere constructively, producing a strong beam.

The diagram on the right shows two light rays emerging from adjacent slits in the grating and heading toward an observer (or a point on a screen) at an angle q from the normal (perpendicular) direction. In traveling to the observer, the ray from the lower slit has to travel an extra path distance; this path difference is . The two rays will interfere constructively only if the path difference is an integer number of wavelengths:

(1) ,

where l is the wavelength of the light and m is any integer. At only those special angles corresponding to integer m's (m=0, 1, 2,...) will the rays from all the slits interfere constructively, producing a bright beam in that direction. In any other direction, the rays from the various slits interfere destructively and produce no light intensity. The integer m is called the order of the diffraction.

An incident light beam made of a several distinct wavelengths will be split by the grating into its component wavelengths, with each separate wavelength heading in different directions, determined by the condition . In this way, the various wavelengths can be determined by measuring the angles.

Bohr model of the hydrogen atom. In the 19th century, it was known that hydrogen gas, when made to glow in an electrical discharge tube, emitted light at four particular visible wavelengths. In 1885, a Swiss high school teacher named Balmer discovered that the four wavelengths, here labeled l_i , where i = 1,2,3,4, precisely obeyed a curious mathematical relation:

(2)                 ,

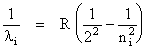where R is a constant, and n_i = 3, 4, 5, 6. The four wavelengths (or "lines") were henceforth called the Balmer lines of hydrogen. Why hydrogen emitted only those visible wavelengths and why the wavelengths obeyed the Balmer formula was a complete mystery.

The mystery was solved in 1913 by the Danish physicist Niels Bohr. According to the Bohr model, the electron orbiting the proton in a hydrogen atom can only exist in certain orbital states labeled with a quantum number n (n=1, 2, 3, 4...). When the electron is in orbit n, the total energy of the hydrogen atom is given by the formula:

(3)                 ,

where c is the speed of light, h is a constant (Plank's constant), and R is a number predicted by the Bohr model to be R = 1.09737 ´ 10⁷ m^-1. The different energies E_n correspond to different orbital states of the electron. Smaller-radius orbits correspond to lower values of n and lower, more negative, energies. The n=1 state is the lowest possible energy state and is called the ground state.

When an electron makes a transition from an initial state of higher energy E_i to a final state of lower energy E_f , the atom emits a photon of energy

(4)                 .

Here we have used the expression for the energy of a single photon: E = hf, where h is Planck's constant and f is the frequency of the light. From equations (3) and (4), the wavelengths of the emitted photon is related to the initial and final quantum numbers like so:

(5)                 .

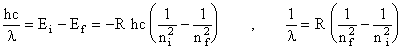This is none other than Balmer's formula! Transitions between any pair of states such that n_i > n_f produces a photon; however, only those transitions with n_f = 2 and n_i = 3, 4, 5, or 6, happen to produce photons in the visible range of wavelengths. Using the measured wavelengths of the Balmer series and equation(5), one can compute the Rydberg constant R.

Experiment

Part 1. Qualitative Observations

Begin by using the "Project Star" cardboard spectrometers provided to examine qualitatively the spectrum of the mercury lamp, the hydrogen lamp, the white light filament, and the overhead fluorescent lights. Record what you see. Note the range of visible wavelengths.

Part 2. Measurement of the wavelengths of the Balmer lines of hydrogen.

Most people can only see three of the four Balmer lines, because the 4th line is faint and very close to the violet edge of the visible spectrum. Observe the hydrogen source through the grating provided. In the first order spectrum (m=1), you should clearly see three lines: red, blue-green, and violet (some people can see a second violet line, if the room is dark.)

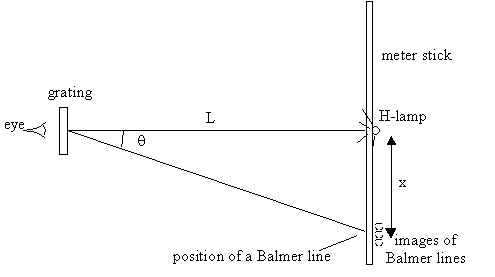Arrange the hydrogen lamp and the diffraction grating on your lab bench, as shown in the diagram. Set them on supports to place them at a convenient height for your eye. Position the grating exactly L=1.00m from the lamp and orient the grating so that it is perpendicular to the line from the lamp (that is, have the grating squarely face the lamp). Place your eye very close to the grating and look through it toward the hydrogen lamp. On both sides of the lamp, you should clearly see the images of the first-order Balmer lines. (Be careful to keep the grating facing the lamp. Move your eye position, not the grating, to see the lines to the side of the lamp.)

With a meter stick as close as possible to the lamp, as shown, measure the x-positions (on both sides of the central position) of each of the three lines as accurately as possible. With your measured L and x's, compute the angle q of each of the first-order Balmer lines. Make a table of your results in your lab book. Leave space for extra columns to add the further calculations below.

The number of lines per mm is marked on the grating. From this, you can compute the spacing d of the grating. Using your measured q 's and computed d, compute the wavelengths of each of the (three or four) Balmer lines. Include a rough estimate of the uncertainty of your wavelengths. Do not report the wavelengths with more precision than you believe.

Finally, with your experimentally determined wavelengths, use equation (5) to determine the Rydberg constant R. Each of your l 's produces an independent value of R. Compute the average R, and from the spread in your values of R, estimate your experimental uncertainty in R. Compare your results with the known value R = 1.09737 ´ 10⁷ m^-1. Does the known value agree with your value, within your experimental uncertainty? If not, can you think of any systematic errors in your measurements that might account for the discrepancy?

Part 3 Solar Spectrum.

If you have time, take the Project Star Spectrometer outside (after signing the sign-out sheet) and observe the solar spectrum by pointing the spectrometer toward a white cloud or at the blue sky near the Sun.

DO NOT POINT THE SPECTROMETER AT THE SUN. DIRECT SUNLIGHT CAN CAUSE EYE DAMAGE.

You will observe that the solar spectrum is continuous (all the colors of the rainbow, like an incandescent light bulb). If you look closely, you will see some dark lines in the spectrum where certain colors are missing. This is an example of an absorption spectrum. The spectrum of the hydrogen lamp and the other lamps you observed were examples of emission spectra. Your TA will explain the difference.

Before leaving, return the Spectrometer to your TA so she can cross your name off the sign-out sheet. No calculations are required for this part.

Pre-lab questions (due at the beginning of the lab period).

1. For a given order (say m=3), is the angle of diffraction for red light larger or smaller than the angle for blue light? Explain.
2. In part 2 of this experiment, how will you determine the spacing d of your diffraction grating?
3. What is the relation between the wavelength l and the frequency f of a photon?
4. What is the relation between the energy E and the frequency f of a photon?
5. Sketch an energy level diagram of the hydrogen atom with the various levels labeled with the proper value of the quantum number n. Indicate on your diagram which transitions cause the four lines of the Balmer series.
6. The colors of the four lines of the hydrogen spectrum are: red, blue-green, and two shades of violet. Which initial states n_i = 3, 4, 5, or 6 correspond to these colors? (Hint: The colors of the visible spectrum, from longest to shortest wavelengths, are: red, orange, yellow, green, blue, violet.)
7. Transitions to the n=1 (ground state) level from higher levels in the hydrogen atom never produce visible wavelength photons. Are the wavelengths produced by transitions to the n=1 level longer or shorter than visible wavelengths? Explain.
8. In part 2 of this experiment, which quantities are given, which are measured directly, and which quantities are calculated?
9. Dry lab.