Experiment 4. Lenses

In this experiment, you will study converging lenses and the lens equation. You will make several measurements of the focal length of lenses and you will construct a simple astronomical telescope.

When a bundle of parallel light rays enters a converging lens, the rays are focused at a point in space a distance f, the focal length, from the lens. A converging lens is convex in shape, that is, thick in the middle and thin at the edges. A diverging lens is concave in shape, i.e. thin in the middle and thicker near the edges.

A converging lens can be used to form an image on a screen of an object. The lens equation relates the focal length f of a lens, the object distance d_o and the image distance d_i ,

. (1)

(This equation can used for both converging and diverging lens; the only difference is that the focal length f is positive for converging lenses, negative for diverging lenses.)

In the diagram above, the points labeled F are the focal points of the lens. The lateral magnification m of the image is defined as . From the diagram above, one can show that m can also be written as .

In this lab, you will use three different techniques to measure focal lengths.

Method I: Use the lens to form an image of an object, measure the distances d_i and d_o, and then use eq'n (1) to compute f.

Method II: Place a point source of light at the focal point of a converging lens to produce a collimated (parallel) beam of light, as shown below. When the location of the point source is adjusted so that the beam coming from the lens is perfectly parallel, then the distance from lens to source is the focal length.

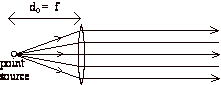
Equation (1) can be applied to this situation. The point source is the object and the object distance d_o is the focal length f. With d_o = f, equation (1) predicts that . The rays from the lens converge "at infinity".

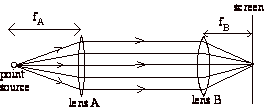
Method III: Once a point source and a lens has been set up to produce a collimated beam, as shown above, then the focal length of another lens can be easily measured. Place the new lens (lens B) in the collimated beam and see where the rays are brought to focus. The distance from lens B to the focal point is f_B, the focal length of lens B.

In the last part of this lab, you will construct a simple astronomical telescope. The astronomical telescope consists of two lenses: an objective lens with a long focal length f_o, and an eyepiece lens with a short focal length f_e . The objective lens forms an image of a distant object (an object "at infinity"). By the lens equation, if the object distance is , then the image distance is . This image, which appears a distance f_o behind the objective lens, is called an intermediate image, because it is intermediate between the objective and eyepiece lens. The observer views this image through the eyepiece lens which acts as a magnifying glass.

The angular magnification M of the telescope is defined as the ratio , where (as shown in the diagram below) q^' is the angular size of the image as viewed by the observer through the telescope and q is the angular size of the distant object as viewed without the telescope.

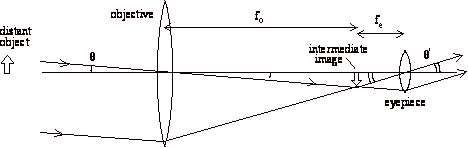
Notice that the distance between the two lenses is . From the diagram above, one can show that the angular magnification can also be written as , the ratio of the focal lengths of the objective and eyepiece lenses.

Procedure

In this lab, you will use an optics bench, which is simply a rail, on which lenses are placed, with a ruler on the side for measuring distances. The other equipment includes a bright light source, which acts nearly like a point source, and three converging lenses labeled A, B, and C. There is frosted glass screen, labeled "I", on which you can view images. Finally, there is a metal plate with an aperture (a hole) in the shape of an arrow. The hole is covered with a frosted, translucent material (scotch tape). When this aperture is placed in front of the light source, it forms a convenient object for image-forming experiments.

Part I Images and Magnification.

In this part, you will use Method I to measure the focal length of lenses B and A.

(1) Place the light source at the end of the optics bench and attach it with the thumbscrew in the slot. Place the arrow aperture on the front of the light source; there is a magnet to hold it in place. It will save a little trouble in your calculations if you position the source so that the object (the frosted arrow) is exactly beside an integer mark (e.g. 2.0 cm) on the scale of the bench. Gently tighten the thumbscrew to secure the source, and record the position of the object. Connect the light source to the power supply and momentarily depress the "start" switch to turn on the light.

Place the frosted screen, I, at the far end of the bench and note its position, as indicated by the ring inscribed on the housing. Again, it will save some trouble if you locate it a convenient integer mark, like 90.0 cm or 92.0 cm.

Now put lens B on the bench close to the light source and move it slowly away from the source until you see a clear image on the screen. The image is most easily seen looking through the screen towards the light source, but it can also be seen from the other side. Adjust the position of the lens to give the sharpest image and record the position of the lens (as indicated by the ring on the housing). Calculate d_o, d_i, and from equation (1), the focal length f_B.

(2) If the image is not centered on the screen, adjust the position of the object plate on the front of the light source until the image is centered. Now measure h_o and h_i, the heights of the object and image. Compute the lateral magnification and compare with the expected value .

(3) Move the lens B to the screen end of the bench and then slide it away from the screen until you get a sharp image on the screen. Repeat the measurements above for d_o, d_i, h_o, and h_i. Recompute f_B and m. Compare your measurements in parts (2) and (3).

(4) Measure the focal length f_A of lens A using method I (don't bother with the magnification m).

II. Use of a collimated beam

(1) Here you will use method II to measure the focal length of lens A. Remove the frosted arrow plate from the light source. The source itself is very small and can be considered to be a point source. Readjust its position so that the source is at a convenient integer mark on your bench. Now place lens A close to the source and slide it away until it produces a parallel, collimated beam. A good way to check that it is parallel is this: Point the beam at a nearby wall where it will produce a disc of light. Adjust the position of lens A until the diameter of the disc is exactly that of the lens opening. Now measure the distance from the point source to the lens; this is the focal length f_A. Compare your measurement of f_A with your previous value. Compute a final best value.

Now you will use method III to measure the focal lengths of lenses B and C.

(2) Without moving lens A, place lens B just beyond A, at a convenient integer mark, and put the frosted screen beyond B. Now move the screen until you jet a sharp image of the point source on the screen. The distance from lens B to the screen is f_B.

(3) Repeat step (2) with lens C in place of lens B.

III. The astronomical telescope.

Choose the lens with the longest focal length. This will be the objective lens with focal length f_o . Also choose the lens with the shortest focal length. This will be the eyepiece with focal length f_e. Place the eyepiece at one end of the optics rail and place the objective lens a distance from the eyepiece.

Aim the telescope towards the far end of the room, where there is an arrow and a graduated scale mounted on the wall, and adjust the telescope position until you can see the arrow through the telescope. It may be difficult to find the image since your telescope has a narrow field of view. Also, you may need to adjust the position of the eyepiece lens to get a sharp image. Is the final image you are looking at upright or inverted? Real or virtual? Explain your answers with words and diagrams.

Once you have found a clear image looking through the telescope, open your other eye so that you can look simultaneously at the enlarged image with one eye and the unenlarged image with the other eye. If you position the telescope just right, you can see the two scales side by side and hence estimate the angular magnification M of your telescope. Compare your answer with the theoretical value of M .

Pre-Lab Questions (due at the beginning of lab).

1. What is the definition of the focal length of a converging lens? Illustrate your answer with a diagram.

2. Consider a lens with a focal length of f =20.0 cm which is used to image an object of height h_o = 3.0 cm, a distance d_o = 40.0 cm away. On graph paper, draw a diagram showing the size (h_i) and position (d_i) of the image formed by this lens. Check that the value of d_i obtained from your graph agrees with a calculation of d_i made by equation (1).

3. In the diagram on page 4.1, show that .

4. What is a collimated beam? Draw a sketch showing how you could produce one. Could you make a collimated beam using only a point source and a diverging lens?

5. An astronomical telescope has an objective lens with a focal length of 600mm and an eyepiece lens with a focal length of 20mm. What is the angular magnification of this telescope?

6. Dry lab.