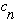Physics 2140, Fall '95
Hints for Homework #11 (Due Wed, Nov 15)
1) We did this in the lecture, and Boas does it too - it's just a
question of following through the logic, and writing it up IN YOUR OWN WORDS!
The point here is not to copy me (or Boas), but work it through yourself so you
really understand every step!
2a) Sketching over several periods means more than just 1 or even 2
periods. I want to clearly see what this periodic function looks like.
Note that the result you get for
 has some simple form which only cares if n is even or odd, but the result you
get for
has some simple form which only cares if n is even or odd, but the result you
get for
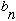 is
NOT completely determined just by knowing if n is even or odd! (There IS a
simple pattern which repeats, but you need to figure out what happens for the
first 4 cases separately. Can you convince yourself that the pattern repeats
every 4 integers?)
is
NOT completely determined just by knowing if n is even or odd! (There IS a
simple pattern which repeats, but you need to figure out what happens for the
first 4 cases separately. Can you convince yourself that the pattern repeats
every 4 integers?)
2b) Is this function even, or odd? If so, you can use what we learned in class
to skip some calculations. (Please indicate in words why you don't bother with
some integrals!)
Note: this integral can be looked up, or else use the famous integration by
parts formula:

3 Again, you can use integration by parts, also with u=x. (What is v here? )
Verify means take your final answer in terms of Exp(i n theta), rewrite in
terms of sin and cos, regroup, and see that your answer is identical to what
you got in 2b.
4a) If you understand Dirichlet's theorem, part a should be doable by
inspection!
b) Just write out the formula for
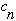 and
and
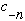 .
Think about what the complex conjugate does to the expression for
.
Think about what the complex conjugate does to the expression for
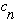
5. If you claim that the answers are not unique, then simply come up
with a different pair of even and odd functions that add up to the same
thing. But if you claim that your answers are unique, can you prove it?
6. Look at the class notes (in the library, or by my door) - I coded up a
similar (but slightly simpler) case for the class demo! My definition of f
wasn't very general, but is good enough for this problem.
 has some simple form which only cares if n is even or odd, but the result you
get for
has some simple form which only cares if n is even or odd, but the result you
get for
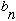 is
NOT completely determined just by knowing if n is even or odd! (There IS a
simple pattern which repeats, but you need to figure out what happens for the
first 4 cases separately. Can you convince yourself that the pattern repeats
every 4 integers?)
is
NOT completely determined just by knowing if n is even or odd! (There IS a
simple pattern which repeats, but you need to figure out what happens for the
first 4 cases separately. Can you convince yourself that the pattern repeats
every 4 integers?) 
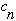 and
and
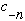 .
Think about what the complex conjugate does to the expression for
.
Think about what the complex conjugate does to the expression for