(Issued Wed, Nov. 15)

Due Wed, Nov 22

Note: Mathematica quiz will be Tues, Nov. 21, at your signed-up-for time.

(If you're going to leave town early for T-giving, please hand in your homework Tuesday, at the exam!)

Reading: Boas Ch 7, 15.4, Start Ch. 8

1a) Give algebraic proofs that for any functions:

i) even times odd = odd.

ii) The derivative of any even function is odd.

b) Boas 7.12.12. Give your answer in Hz, and justify it with a few words of explanation!

2) Boas 7.9.23 Hint: Remember, to make a Fourier sine series, define f for all x to be odd, with period 2L.

Hint: This problem involves some algebra! Do it methodically to avoid mistakes. The answer is in the back, so show your work!...

3) Boas 15.4.3.

4a) Let .

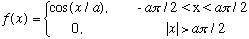Just as in problem 3, find the Fourier transform of f(x) and write f(x) as a Fourier integral.

b) Sketch your results for g([[alpha]]). Roughly how "wide" would you characterize f(x), and g([[alpha]])? Does the product of those widths appear to depend on a?

Hint for #4a:

Hint for #4a: Note that Boas 15.4.11 is the same problem, (except she chooses a=1) so you can check your answer in the special case a=1.

Hint for #4b: A quick sketch is fine, but this is a funky function... I let Mma sketch it for me, and that helped me picture it a bit better! (Is g symmetric? Realizing this helps a lot in sketching it!)