 ,
which gives t=81 s)
,
which gives t=81 s)(Here is the related homework set) (Issued Wed, Nov. 22) Due Fri, Dec 1
For help with solving Differential equations, see e.g. Blachman p. 59, In[51] for a simple example, and In[52] shows an example in which she specifies a "boundary condition". (Note (!) that these equations all use double equals, "==")
In many cases, differential equations can't be solved analytically (i.e., there's no way of writing down y as an elementary function), but there's still a solution, you just can't write down a simple formula for it! Mma can find this as well, with the NDSolve[...] command, which is a "numerical differential equation solver". This requires that you provide a suitable number of boundary conditions, and results in what is known as an interpolating function, which you can plot. See Blachman p. 39 and 40 for an example of this. (I find this feature of Mma pretty useful - maybe you will someday as well!)
Here's an extra credit problem which demonstrates Mma's ability to solve differential equations: (Part of this problem is analytic, and should be done on paper. Later parts will also use Mma.) (10 pts of EC)
A bundle of 2140 homeworks, mass 70. kg, is dropped out of a plane 32. km above
the surface of the earth. For this problem, neglect horizontal motion, and
assume the bundle starts at rest. Take the y axis as positive down. (Note:
without air friction, it's easy to find the time to fall,
 ,
which gives t=81 s)
,
which gives t=81 s)
a) If the force of air resistance is proportional to velocity, show that the
differential equation of motion is
 .
(k is a positive constant). Find v as a function of t. Find the limiting value
of v as t goes to infinity. (This is the terminal velocity). Also show
how to find the terminal velocity directly from the differential
equation (Hint: What is dv/dt after v has reached a constant value?) If a
reasonable value of k is 18.5 kg/sec, what is the terminal velocity? You have
found v(t) = dy/dt. Integrate again to find y(t). If k = 18.5 kg/sec, calculate
the time of fall until ground impact. (Here, you may want Mma to solve this for
you! A graphical solution is fine (round t to the nearest second), or you may
be able to use FindRoot[...])
.
(k is a positive constant). Find v as a function of t. Find the limiting value
of v as t goes to infinity. (This is the terminal velocity). Also show
how to find the terminal velocity directly from the differential
equation (Hint: What is dv/dt after v has reached a constant value?) If a
reasonable value of k is 18.5 kg/sec, what is the terminal velocity? You have
found v(t) = dy/dt. Integrate again to find y(t). If k = 18.5 kg/sec, calculate
the time of fall until ground impact. (Here, you may want Mma to solve this for
you! A graphical solution is fine (round t to the nearest second), or you may
be able to use FindRoot[...])
b) A somewhat more realistic force of air resistance is proportional to the
square of velocity, i.e.
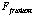 =
-c v |v| (This form ensures that the sign is always correct. In our problem,
convince yourself that v is always positive, so we don't need the absolute
value symbol) Write down the new differential equation of motion. Let c=0.5
kg/m (I claim this yields the same terminal velocity as part a) The equation
for v is a bit nastier than in part a. Let Mma find the velocity as a function
of time. (if you separate variables as in part a, this requires only the use of
Integrate[...]) Let Mma also find the height as a function of time. What
is the time of fall now?
=
-c v |v| (This form ensures that the sign is always correct. In our problem,
convince yourself that v is always positive, so we don't need the absolute
value symbol) Write down the new differential equation of motion. Let c=0.5
kg/m (I claim this yields the same terminal velocity as part a) The equation
for v is a bit nastier than in part a. Let Mma find the velocity as a function
of time. (if you separate variables as in part a, this requires only the use of
Integrate[...]) Let Mma also find the height as a function of time. What
is the time of fall now?
c) To make the problem even more realistic, we can argue that the friction
coefficient c is itself a function of height, scaling with atmospheric density
as
 ,
where h is the height above ground, and H=8 km is the scale height of the
atmosphere. (Let
,
where h is the height above ground, and H=8 km is the scale height of the
atmosphere. (Let
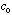 be the value you used in part b) Furthermore, g is not exactly constant, but is
given by
be the value you used in part b) Furthermore, g is not exactly constant, but is
given by
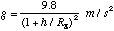 ,
where
,
where
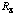 is the earth's radius, about 6370 km. Plot the velocity and altitude as a
function of time. Find the impact time. Explain the differences between part b
and c. Discuss the general behavior of the velocity curve.
is the earth's radius, about 6370 km. Plot the velocity and altitude as a
function of time. Find the impact time. Explain the differences between part b
and c. Discuss the general behavior of the velocity curve.
Note: because g and c are not constants any more, but functions of y, this differential equation can NOT be solved analytically by separation of variables! But NDSolve[...]. works!
Note that NDSolve can solve for two things at once, for example, you can try NDSolve[{diff eq. for v[t], diff eq. for h[t],
b'dry cond for v[0], b'dry cond for h[0]},
{v,h},{t,0,1000}]
And this will give you interpolating functions for both v and h as functions of time. Here, you must indicate that you want v and h as fns of time explicitly, by writing them as v[t] or v'[t] or whatever, in the diff. eq's above. You can plot v with, e.g. Plot[v[t] /. %, {t,0,1000}]. You might want to look up /. (Blachman 7.3) to remember what that is doing.