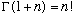(Issued Wed, Nov. 29)

Due Wed, Dec. 6

Reading for this assignment: Boas 8.6, 12.1-2, 12.6-7, 12.9, 12.11-14, 12.19

1. Boas 8.6.14

Hint: See "Use of Complex Exponentials" section in Boas, pp. 364-365. To summarize: if you could solve the related ("secondary") complex equation,

y''+8y'+25y = 120 Exp[5 i x],

what equation would the imaginary part of the latter satisfy?

Hint2: To solve the "secondary" equation I just wrote down, could you first solve y''+8y'+25y=0, and get a general solution? If you then found some particular solution of the "secondary" equation, you could just add it to this general solution...(Particular solutions can often be found by guessing, what's a plausible guess here? Your guess may have some unknown constant in it, but it should turn out to be constrained by the equation)

2. Boas 12.1.2 (Please read Boas' instructions above the problem)

3. Boas 12.1.18

4a) Boas 12.6.4

(Hint: This is meant as a "quickie"!)

b) Boas 12.6.5

(Hint: Boas eqn. 12.2.8 gives the first few Legendre polynomials)

c) Boas 12.7.5

(Note: If l is odd, this problem is trivial. Do you see why?

But, since l is arbitrary, you need to think about Boas' hint...)

5. Boas 12.14.1 and 2

Hint: You may sketch these graphs by looking up the J's in tables, or evaluating them numerically from the power series (note that 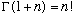) or (by far the easiest!!) by using Mathematica, which has a built in function BesselJ[n,x], which gives the nth Bessel function at point x, .