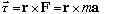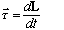Due Wed, Sep 13

Reading for this homework: Boas sections 3.5, 4.1, 4.3, 6.4, 6.5

(also 4.5 and 4.6 if you want more review on derivatives)

For Mathematica: Blachman Ch. 1, and sections 2.1-2.9, 2.13, 4.1

(or, Wolfram 1.1,1.2.1,1.2.2,1.8.1, and 1.9.1 )

Problems:

1 Boas 3.5.19

2. Boas 3.5.26

3. Boas 3.5.30

4. Boas 6.4.2

5a) Boas 6.4.9. (Since 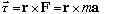, you've just show that !)

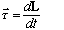b) A 3 kg mass moves around a circle of radius = 1.5m, but not with uniform motion. ( ) Instead, its angle is given by . Using part a, find the torque which must be acting on the particle as a function of time.

Computer Assignment. Use Mathematica to solve the following problems. Please turn in a neat, printed Mathematica notebook, including titles and explanatory text where appropriate. Before printing your notebook, please delete any experimentation/dead ends/thrashing around that you did. An independent party should be able to run the notebook you hand in. (To delete unwanted entries, drag the mouse down the right margin of the material to be deleted to highlight the relevant brackets. Then type command-x. Careful, this can't be undone!) If you want to print just a selection of a notebook, drag the mouse down the right margin of the material to be printed to highlight the relevant brackets . Choose "Print" from the menu in the upper left, and then "Print Selection". A box appears with some choices, and then you can click "Print" again.

6a. Find numerical values for cos([[pi]]/4), for [[radical]]2, and for e^{[[pi]] [[radical]]163}, all to 30 digits. Next, note that the following beast is inherently ambiguous:

3 ^{2 4}. Using appropriate parentheses, let Mathematica evaluate both possibilities for what it might mean. Then enter it without parentheses, to see how Mathematica chooses to resolve the ambiguity.

b) Consider the function f = x^4 - 2x^3 - 2x^2 + 4x. How many times do you expect this function to cross the x axis? Use the function Plot[...] to make a graph to check your prediction. Also, by plotting with increasingly narrow ranges for x, find the numerical value of the left-most zero of f (to 2 significant figures)

c) You can find the roots numerically in various ways.

NRoots[f == 0, x] works when f is a polynomial. Try it.

Solve[f == 0, x] gives "symbolic" solutions when possible. Try it too.

FindRoot[f == 0, {x,xstart}] will generally look for the root "closest" to xstart. Try this, with xstart = -1, to find the first zero of f. What happens if you use xstart = -.7?, -.8?, -.9? (Look carefully at the answer with xstart = -.8!! So, be warned! FindRoot doesn't ALWAYS find the closest root...)

7. Mathematica (from now on, "Mma") represents vectors with braces, so the vector v = (a,b,c) is v = {a,b,c} in Mma. Furthermore, the vector components v1, v2 (or vx, vy) are called v[[1]], v[[2]], etc.

a) Let Mma find the product of a scalar k and the vector (a,b,c)

(If you're not sure how, just experiment!) Also, let Mma add vectors (a,b,c) and (d,e,f).

b) Let Mma find the time derivative of the vector

r(t) = (a cos(wt), b sin(wt), ct) (To take a derivative of a function f with respect to t, you use the notation D[f, t])

Describe (in words) the path followed by this vector as time evolves.

Let Mma extract the 2nd (i.e, y) component of the result for r(t).