Physics 2140, Fall '95
Homework #3
Due Wed, Sep 20
Reading for this homework: Boas sections 6.6, 6.7, 6.8
For Mathematica: Blackman 3.2, 3.5, 4.2.0, 4.6
1) Boas 4.1.5 2) Boas 4.13.5
3a) Boas 6.6.5 3b) Boas 6.6.8b only
4) 6.6.13 5) 6.8.6
6a) Use MMA to check your answer to 1)! You can do this however you
like, here are some features of Mma that I found useful for doing this: The
derivative function you used last week can be used for partial derivatives too,
with D[f,x] giving
 .
(You can also assign a name to expressions you want to use again, e.g. w =
x^4+... or dwdx = D[w,x], etc.) (Don't begin your names with
capitals, these are reserved for Mma!) You will also need to know how to solve
a set of equations, here's one way: Solve[{eqn1,eqn2}] ,
or more specifically
.
(You can also assign a name to expressions you want to use again, e.g. w =
x^4+... or dwdx = D[w,x], etc.) (Don't begin your names with
capitals, these are reserved for Mma!) You will also need to know how to solve
a set of equations, here's one way: Solve[{eqn1,eqn2}] ,
or more specifically
myanswer = Solve[{expression ==0, another expression
== 0}].
(Note the double equal sign in this particular context!)
Finally, you may "plug" in the results of a Solve into an expression:
<Some expression> /. myanswer (That is a slash and a
period, which you can read as "at the point"). If the "Solve" gave multiple
possible results, then you will get a list of the resulting different answers.
("Some expression" above can of course be one you previously named, e.g.
dwdx /. myanswer should probably give 0 in this case...)
Note: Mma "knows" about complex numbers, i.e. it happily takes
 ,
and calls this I. (You may not have thought of complex solutions to #1: that's
fine for now since we haven't studied imaginary numbers, but Mma finds them
anyway!) My version of Mma is apparently confused about solving cubic equations
like this, and so repeats one of the roots several times.(?)
,
and calls this I. (You may not have thought of complex solutions to #1: that's
fine for now since we haven't studied imaginary numbers, but Mma finds them
anyway!) My version of Mma is apparently confused about solving cubic equations
like this, and so repeats one of the roots several times.(?)
6b) In my solution to Boas 6.8.6b, I needed a trig integral. (Did you?) Let's
let Mma do it! Evaluate Integrate[
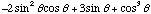 ,{
,{ ,
0,
,
0,
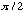 }].
(You will have to use a dummy variable for
}].
(You will have to use a dummy variable for
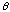 )
Feel free to use Mma to solve hairy integrals throughout this course, and in
the future too!
)
Feel free to use Mma to solve hairy integrals throughout this course, and in
the future too!
7a)Plotting in 3D. Mma has many cool built in plotting functions. Let's
try to get a better picture of the nasty looking function from problem 4 (Boas
6.6.13)
First, take a look at it in 3-D over the range,say, -2<x<2,
-4<y<4:
Plot3D[function from prob 4, {x,-2,2}, {y,-4,4}];
Next, generate a contour plot of this same thing. You should name the
plot (you'll see why below -- choose any name you like), something like this:
cpf = ContourPlot[fn from prob 4, {x,-2,2},
{y,etc}];
7b) Gradients. Mma can calculate gradients, but you can just about as
easily do it by hand. (Also, the built in grad assumes functions in 3-D,
but here we're looking at a 2-D function.) Use D[] to build the gradient
of this same scalar function (Boas 6.6.13). Remember, the gradient is a vector
(see previous Mma hw!). Call it something, e.g. gradf = {D[..., x], D[...,
y]}
Does this agree with what you got for problem 4?
7c) Plotting vector fields: Mma is, among other things, a
programming language, and many people have written many nifty Mma "programs".
Some of these come with Mma, but you still need to "load them in" to use them.
(There are so many, that it would take too long if Mma loaded all possible
packages every time you started it up!) Today we'll use a graphing package
called PlotField. To load it in, type Needs["Graphics`PlotField`"]
Everything must be JUST right, use back single quote "`" (located at the
upper left of the numerical pad, which is on the right side of the NeXt
keyboards) and get the caps right, etc. This reads in many fancy 3-d plotting
routines, including one called PlotVectorField. We will use this to plot the
gradient of the field you looked at in 7a, calling the plot something else,
e.g:
pgf = PlotVectorField[gradf,{x,-2,2},{y,-4,4}, PlotPoints -> 10]
(PlotPoints is one of many available options, see the next question!)
Warning 1: This may take a minute! Even with only 10x10 points, it's slow.
Warning 2: If you try typing PlotVectorField[...] before
you have typed Needs[...], you're in trouble! Typing
Clear[PlotVectorField] and then redoing the Needs[...] may work -
read Blachman 7.2 if this happens...
7d) Use Options[<any Mma command>] or
??<any Mma command> to learn about options to Mma
functions. Take a look at all the plotting options available to ContourPlot.
Go back and add e.g. FrameLabel -> {"x","y"},
ContourShading-> False (and any other options you want) for
the contour plot. The format is just to add these statements, after commas,
inside the square brackets of the command. (See Blachman 4.2 if you have
troubles)
(FrameLabel adds labels to the axes, to make it look nicer. I found the
ContourShading default (True) to be distracting)
Finally, type Show[pgf, cpf] to plot them both, and you can see the
field and its gradient together. (That's why it's nice to give graphs a name -
you can look at them again without recomputing them!) Does this help you
visualize what was going on any better than before? What can you say about the
relative orientation of contour lines and gradient vectors? Does the direction
of the arrows tell you anything interesting?
 .
(You can also assign a name to expressions you want to use again, e.g. w =
x^4+... or dwdx = D[w,x], etc.) (Don't begin your names with
capitals, these are reserved for Mma!) You will also need to know how to solve
a set of equations, here's one way: Solve[{eqn1,eqn2}] ,
or more specifically
.
(You can also assign a name to expressions you want to use again, e.g. w =
x^4+... or dwdx = D[w,x], etc.) (Don't begin your names with
capitals, these are reserved for Mma!) You will also need to know how to solve
a set of equations, here's one way: Solve[{eqn1,eqn2}] ,
or more specifically  ,
and calls this I. (You may not have thought of complex solutions to #1: that's
fine for now since we haven't studied imaginary numbers, but Mma finds them
anyway!) My version of Mma is apparently confused about solving cubic equations
like this, and so repeats one of the roots several times.(?)
,
and calls this I. (You may not have thought of complex solutions to #1: that's
fine for now since we haven't studied imaginary numbers, but Mma finds them
anyway!) My version of Mma is apparently confused about solving cubic equations
like this, and so repeats one of the roots several times.(?)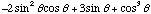 ,{
,{ ,
0,
,
0,
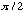 }].
(You will have to use a dummy variable for
}].
(You will have to use a dummy variable for
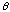 )
Feel free to use Mma to solve hairy integrals throughout this course, and in
the future too!
)
Feel free to use Mma to solve hairy integrals throughout this course, and in
the future too!