 above the xy plane, plus a circular base in the xy plane. An electric field E
is given by
above the xy plane, plus a circular base in the xy plane. An electric field E
is given by
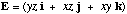 .
Evaluate directly (as a surfact integral) the flux of E out of S, defined to be
.
Evaluate directly (as a surfact integral) the flux of E out of S, defined to be
 ,
where n is the unit normal vector pointing outwards from the surface.
,
where n is the unit normal vector pointing outwards from the surface.(Issued Wed, Oct 4)
Due Wed, Oct 11
Reading: Boas Ch. 6.10, Blachman 4.6
1a) Consider the closed surface S consisting of the hemisphere
 above the xy plane, plus a circular base in the xy plane. An electric field E
is given by
above the xy plane, plus a circular base in the xy plane. An electric field E
is given by
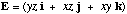 .
Evaluate directly (as a surfact integral) the flux of E out of S, defined to be
.
Evaluate directly (as a surfact integral) the flux of E out of S, defined to be
 ,
where n is the unit normal vector pointing outwards from the surface.
,
where n is the unit normal vector pointing outwards from the surface.
b) Use the divergence theorem to find the flux by evaluating the appropriate volume integral. (Much easier, no?!)
2 Given
 :
:
a) Evaluate
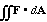 over the surface of the sphere
over the surface of the sphere
 .
.
b) Find
 .
(Boas Eq'n 7.7.2, if you've forgotten...)
.
(Boas Eq'n 7.7.2, if you've forgotten...)
c) Evaluate
 over the volume inside the sphere given in part a. Should your answers to a and
c agree? Do they?
over the volume inside the sphere given in part a. Should your answers to a and
c agree? Do they?
Hint for c: The volume element
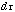 in spherical coordinates is given by Boas Ch. 5.4.7:
in spherical coordinates is given by Boas Ch. 5.4.7:
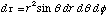
(For the next 2 problems, Boas says "use either a volume integral or a surface integral, whichever is easier". This is fine with me. However, if you feel shaky about these surface and volume integrals, its a great exercise to do the problems both ways, and check that your answers agree!)
3) Boas 6.10.3
4) Boas 6.10.6
5) Boas 6.10.12 (Hint: Although I didn't do this example in lecture, I did write it up in my lecture notes! They're in the library, and also outside my office door, as usual)
6) Earlier, we used Plot3D to look at a graph of a scalar function in 3D perspective. Mma can also generate parametric plots in 3D. In class, we talked about (and used) parametric curves when we did line integrals, but one can also parametrize surfaces as well. The relevant Mma command is ParametricPlot3D[{x,y,z},{t,tmin,tmax},{r,rmin,rmax}]
where x,y,z must be functions of the parameters r and t. (If you leave out the last list, {r,...}, then you will get a line rather than a surface, as you might expect.) Unfortunately, Blachman doesn't talk much about this function (see however p. 75 for 2-D parametric plots. Wolfram p. 168 and 839 may also be useful)
a. Let the parameters be cylindrical coordinates r and t, such that
x=r cos(t), y=r sin(t), and z will be specified. Plot a circle (a circular line, not a surface!) of radius 2, located 5 units above the x-y plane. Hint: After defining x and y properly, e.g. x = r Cos[t], etc., and setting z and r appropriately, the plot would be given by ParametricPlot3D[{x,y,z},{t,0,2Pi}]
b. Now, plot a surface which is a disc of radius 2, again 5 units above the x-y plane.
(Hint: Recall, r=. makes Mma forget it ever knew what r was.)
c. Now plot a cone of height 5, with its tip at the origin, axis on the positive z axis, and base radius 2 units. [Hint: z depends on r now!]
Next, using what I describe below, change the default view for the last figure, showing a view directly in front of the cone
You can get pictures from different view points using Show[%,ViewPoint->{x,y,z}], where x,y,z are the coordinates of your new viewpoint. Mma can really help here, with the "3D Viewpoint Selector". To find this panel, select Action in the Mathematica menu, then Prepare input, and finally 3D Viewpoint Selector. The panel shows a cube, which you can rotate by using the three coordinate sliders. (You can choose Cartesian or spherical coordinates to do this. In this case, you should use Cartesian) Once you've found a good viewpoint, just put its coordinates into the Show command above. You can do this by hand, but Mma can do it for you. Just get the desired command into the window called "Text to Insert". If you click and drag on the button below this window, you will find you can choose the above Show command all ready to go! Once you have the command in the "Text to Insert" window, click on "Insert" and the command is inserted back into your notebook, ready to execute. (You may want to add a semicolon at the end by hand, and may have to change the % to %<whatever>, if you've executed other commands since your last 3D plot)
d. Plot the surface of a cylinder of radius 2 (just the round part, not the
caps), with height 5. Then, modify this surface so that its top is no longer at
the fixed height 5, but rather is given by
 (Note: This last may seem a bit tricky, but there is a fairly simple solution.
Play with it, and think a bit about what it should look like, so you can be
sure you've got it right)
(Note: This last may seem a bit tricky, but there is a fairly simple solution.
Play with it, and think a bit about what it should look like, so you can be
sure you've got it right)