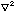(Issued Wed, Oct 11)

Due Wed, Oct 18

Reading: Boas Ch. 6.11, Blachman 4.8, 6.1, 6.10

1a) Boas 6.10.11 1b) Boas 6.10.16

2. Calculate the Laplacian 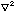of the following two scalar functions:

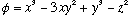, and 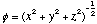. Which of these 2 functions could conceivably be an electrical potential in a region of space with no charges? Very briefly, why? (Reminder: 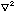is given in Boas 6.7, eq'n 7.4)

3. Boas 6.11.2

4 Boas 6.11.3

5 Find, the easiest way you can: (Think! before you start doing any hairball integrals)

a) 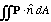over the upper half of the sphere r=1, if .

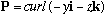b) 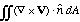over the surface consisting of the four slanting faces of a pyramid whose base is the square in the (x,y) plane with corners at (0,0), (0,4), (4,0), (4,4) and whose top vertex is at (2,2,3). Here,

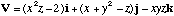
6. Mma has nice tools for generating lists of data, and plotting lists of data (rather than plotting formulas, which is all we've done so far)

a) Using the Table[...] command (Blachman, p. 119), display the list of numbers {0.2, 0.4, 0.6, 0.8, 1.0} Next, construct a list of numbers from 0 to 2[[pi]] in increments of 0.01[[pi]]. Call this list list1. Be sure to suppress the output (with a ; a semicolon at the end) or you'll have numbers filling your screen!

b) Construct the Cos of these values, calling this new list c1. Again, you want to suppress the output! Mma's Cos function is "listable" (Blachman p.129) which means that making c1 should be VERY easy, you don't need to use the Table command again. Now plot c1 using the ListPlot command. (Blachman, section 4.8) It should look like a nice cosine curve.

c) But look at your x axis - something is wrong! Listplotting a simple list of y values, Mma assumes that the corresponding x values are 1,2,3,..., not what we really want. Fortunately, ListPlot can also take as argument a list of points, ListPlot[{ {x1,y1}, {x2,y2}, ... }] which does just what we want. So, construct a new list of points, called list2 = { {x1,y1}, {x2,y2}, ...}, where here x1, x2, ... should be the x points of list1, and y1, y2, ... should be the y points of c1. (This may take some thought, and may require using a Table command again) Now run ListPlot[list2], it should look better. Also, try ListPlot[list2, PlotJoined -> True].