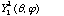(given in F+T table 11-2) is properly normalized.Due Wed, Apr 26
(last hw, heck yeah!)
Required reading for this week: F+T Chapter 11.1, 11.2 (+11.3 for your cultural edification.) (Optional: Beiser through 6.7)
2. F+T 5-6a
3. F+T 5-7a
4. F+T 5-8
5a) Verify that for the case l=1, m=1, the spherical harmonic function
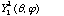(given in F+T table 11-2) is properly normalized.
b) Suppose that a bound-state energy eigenfunction has the form
where
is a normalized spherical harmonic. What is the normalization condition on
R(r)? Why?
c) From F+T table 11-2, the spherical harmonic function for l=2, m=0 is
.
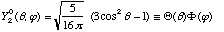Since m=0,. what can you say about the form of
?
Show that
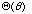indeed satisfies the differential equation for
,
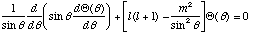(with l=2, m=0.)