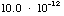Due Wed, Feb 1

Required reading for this week: F+T Chapter 1.1-1.3, 1.6

(Optional: Beiser, Ch. 2)

1) F+T 1-1

2) F+T 1-3

3a) What is the energy and momentum of an x-ray photon whose wavelength is 10.0 pm (= 10.0 picometers = 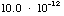m)?

b) If these 10.0 pm photons are scattered from a target by the Compton effect, what wavelength and momentum will the outgoing x-ray photons have if they are observed 90 degrees from the incident beam?

Assume the target is made of iron, Fe, with an atomic weight of 56 amu.

c) What is the Compton wavelength ( h/mc) of iron atoms?

d) If our 10.0 pm photons scatter not from the electrons, but rather from the Fe atoms, what wavelength and momentum will the outgoing x-ray photons have if they are observed 90 degrees from the incident beam? How does this wavelength compare with parts a) and b)?

4) In part b) of the previous question (10.0 pm photons, scattering 90 degrees off of electrons in a target) what is the energy of the recoiling electrons? (Hint: Recall, 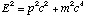for relativistic particles)

5) We talked in class about Planck's radiation formula for blackbodies, namely 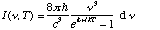is the spectral energy density as a function of the frequency, , of the emitted light. (k is Boltzman's constant, T the temperature in Kelvins, and h is Planck's constant.) Rewrite this formula in terms of wavelength, i.e. find .

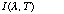(Hint: Use , and don't forget that the differential .

b) For large wavelengths, show that your formula reduces to the Rayleigh-Jeans law, 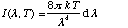(Hint: Recall that 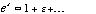for small .) Also, for short wavelengths, show that your formula goes to 0.

6) Warmup Computer Assignment. You may use any programming or graphics system you like - you will probably find Mathematica (henceforth "MMA",) the simplest, and I encourage you to use it. Please turn in a neat, printed output (e.g. a Mathematica notebook) including titles and explanatory text where appropriate. (You may write these in by hand if your system doesn't allow it otherwise.) Before printing your output, please delete any experimentation/dead ends/thrashing around that you did. An independent party should be able to understand, and even run what you hand in to reproduce the results.

Generate a graph of the spectral energy density as a function of frequency, , for T=2.7 K. Chose your range appropriately, so you can clearly see the "whole" curve. (Note that 2.7 K is about the temperature of the "universe" today. The curve you generate has been experimentally measured by the COBE satellite to very high accuracy. It fits like a charm!)