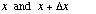 goes to
goes to
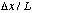 ,
independent of x. (which is precisely the classical
expectation.)
,
independent of x. (which is precisely the classical
expectation.)Due Wed, Mar 8
Required reading for this week: F+T Chapter 3.5-3.11, 5.7
(Optional: Beiser, Ch. 5.4-5.7)
1. F+T 3-6. (Use the infinite square well solutions, i.e. the particle-in-a-box equations, NOT just the uncertainty principle for this one.)
2. F+T 3-9
3. F+T 3-10
In addition: 3c) Find the expectation value <x>
(Hint: Do you really have to do any integral?)
4a) In class, I made a handwavy defense of the correspondence principle: namely, that as n -> infinity, the quantum particle-in-a-box gives the same results as classical particle-in-a-box.
Sharpen this up, by showing that as n -> infinity, the probability of
finding a quantum particle (in a box of size L) between the positions
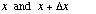 goes to
goes to
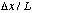 ,
independent of x. (which is precisely the classical
expectation.)
,
independent of x. (which is precisely the classical
expectation.)
b) An important property of eigenfunctions
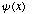 of a system is that they are orthogonal to one another, i.e.
of a system is that they are orthogonal to one another, i.e.
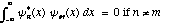 .
(Here,
.
(Here,
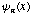 is the wavefunction correesponding to the nth energy eigenvalue)
is the wavefunction correesponding to the nth energy eigenvalue)
Verify this orthogonality relation, for the specific case of the eigenfunctions of a particle in a one-dimensional box.
5a) A particle in a box that runs from 0 to L should have
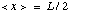 by symmetry. Verify that this is correct no matter what n is.
by symmetry. Verify that this is correct no matter what n is.
Then, calculate
 for the nth wavefunction.
for the nth wavefunction.
b) Show that in general, given some distribution of positions x,
 .
(This quantity represents the deviation from the average, and can be
used as a more rigorous definitition of what we mean by the uncertainty in the
position, or
.
(This quantity represents the deviation from the average, and can be
used as a more rigorous definitition of what we mean by the uncertainty in the
position, or
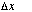 .
.
c) Combine a and b, to find the uncertainty in the position of a particle in a box of size L, when n=1. What is the limit as n-> infinity?