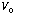Due Wed, Mar 22

Required reading for this week: F+T Chapter 4. (Optional: Beiser 5.7)

Reminder- 2nd midterm: Thur. evening, Mar 23 7:30-9 Muen E-131.

(Any possible conflicts must be discussed with me BEFORE Mar 17!)

1. F+T 4.1

2. An electron is trapped in a finite 1-dimensional square well, of width

L = 1 Angstrom, and has a total ground state energy of 10 eV.

a) What must the height of the well, 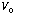, be? (In eV)

b) Can this electron be excited into a higher state, and still be trapped?

Why or why not?

Hint: You should not need to use Mma for this problem, though a calculator will be useful. (In fact, # 5 below is going to ask you to CHECK your answer with Mma)

3. F+T 4-2

4. F+T 4-3a and b. Note: If you want, you can certainly write a computer program for this, or use Mma. (In this case, you should probably work problem number 5 first!) On the other hand, for part a, a careful plot, plus a few tries on your calculator to home in on the exact answer, will be o.k. For part b, I managed to find an analytic solution. It required a bit of algebra, but nothing you can't handle. So, it's up to you. In any case, give answers to 2 or 3 significant figures throughout.

5. In class last week, I showed you how to solve for the energy and wave function of a particle in a box, with Mma. Here's the code I used for that demo:

u[x_] := Which[ x < -2., 5. ,

x < 2., 0.,

True, 5. ];

e=.40987;

soln = NDSolve[{p''[z] == (u[z] - e) p[z],

p[0.]== 1.,

p'[0.]== 0.}, p, {z,-5,5}];

Plot[p[x] /. soln,{x,-4,4}, PlotRange -> {-2,2}];

(I checked it with the following command, some version of which could prove useful to you in problem 4-2 and 4-3 above, or part d below)

FindRoot[Tan[2. Sqrt[ee]] == Sqrt[5/ee - 1.] , {ee,.41}]

Mma is picky about syntax! Be sure you properly input things like capitals, double equals, curly vs. square brackets, etc. You should probably begin by copying the above in, and make sure that you get a correct looking result. You should really understand what is going on with this code. If you don't, ask me or a fellow classmate! Feel free to play a little bit, to get a feeling for what happens if you choose the wrong energy.

My well is centered about the origin. Be sure you understand exactly what "L" is in this case. Also, my boundary conditions (p[0], and p'[0] above) are designed to find the ground state. If you need excited states, you must think about what might have to change. Finally, I was solving the differential equation (with u= 5 outside the well, which ran from z=-2 to +2). This was a pure mathematical expression, everything was unitless! But of course, we really want to solve the Schrodinger equation, which looks almost like this, but has units in it: .

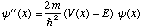a) If I define z = x/L (i.e, I measure distance in units of L), then I claim . (where primes mean derivatives with respect to the argument of the function) Show this formula is correct.

b) If I define and , then I claim that u and e are unitless (show this is true) and the differential equation I was solving in MMA is exactly equivalent to the correct Shrodinger equation. (show this is true, too)

c) Armed with the above, check your answer to problem #2, by modifying u[z] appropriately, (are the z limits correct?) and see whether the ground state energy E=10 eV (modified appropriately to give you ) actually does give you a proper looking ground state. Submit a graph that indicates you've done this succesfully. You should include (either in the Mma notebook, or on a separate sheet) the calculations you used to convert from V to u, and E to e.) (If and only if you simply couldn't solve problem #2, you may use

V=38.3 eV, E = 13.6 eV)

d) Finally, modify your well to be 150 eV deep, rather than using the value from problem 2. Now find the new ground state energy, and also the first excited energy. Submit graphs to show the corresponding wavefunctions too. (If it takes you lots of guesses before you home in on the right energy, please save a tree and CHOP MOST OF THE WRONG GUESSES out of your Mma notebook.) It may give you some confidence to check your answer, see F+T 4-3b, and 4-4b. (That's what the last line of my sample code above was doing)