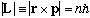Issued Wed, Feb 7 Due Wed, Feb 14

Required reading: F+T Ch. 1, 2.1-2.3 (Optional: Beiser Ch. 4, 3.1-3.4)

1) (15 pts) In class, we derived formulas for the Bohr atom by appealing in part to experiment (we assumed and made use of the Balmer/Rydberg formula) This is not necessary if we make one extra fundamental assumption, namely, that angular momentum is quantized. Mathematically, this means: 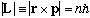, where n is an integer.

a) For a circular electron orbit, show that this formula leads to ,

while Newton's classical law for a circular orbit (assuming only that the centripetal force comes from the electrical force law) leads to

.

b) Eliminate v from these two equations, to come up with a formula for the radius. It will depend on the integer n, just like what we got in class.

Write your expression as , and so find the formula for (the "Bohr radius") in terms of fundamental constants. Plug in numbers to find the value numerically. (It should be around .5 Angstroms)

c) In class we showed that the total energy of an electron in a circular orbit (kinetic energy + potential energy) is . Sketch how that (purely classical) derivation goes. The important part is to get the sign right, as well as that funny factor of 2. (What does a negative energy mean?)

d) Combine your results from parts b and c to derive the formula for the quantized values of energy in a hydrogen atom.

Rydberg's empirical observation was that light from hydrogen has . Show that your formula gives just this result, and so find the Rydberg constant, 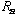, in terms of fundamental constants. Plug in numbers to find the value numerically. (It should be around 109,700 /cm)

e) De Broglie's postulate (that the wavelength of a particle is given by 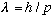) is an even more fundamental starting point for the Bohr model. If de Broglie is right, then you expect that an integer number of wavelengths of an electron should fit exactly into the circumference of its orbit, i.e. . Show that this leads directly to . (Thus, given all your work above, de Broglies hypothesis is a sufficient starting postulate to get the Bohr atom from scratch!)

2a) How many revolutions would an electron in the n=2 state of a hydrogen atom make before dropping to the n=1 state? (Assume the average lifetime of the excited state i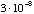s sec. Your results from 1a and b give you the velocity and radius, which may be useful) In a planetary picture of the hydrogen atom, you have just learned how many "years" an electron circles steadily before it changes orbits.

b) What is the classical frequency of an electron in the n=100 state of hydrogen? (i.e, the number of revolutions per second) What is the frequency of the emitted photon predicted by Bohr if this electron drops into the n=99 state? Does Bohr's correspondence principle work?

3. F+T 1-26

Hint: Prob.1 should help. ( 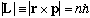is still true even in a muonic atom)

4 Suppose we did a Franck-Hertz experiment, but instead of mercury vapor, we use hydrogen gas vapor. Let the accelerating potential be set at around 12.1 V. Would we be near a minimum of current? (Why or why not?) What wavelength(s) of light would the hydrogen gas emit?

5a) The wavelength of the 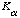x-ray line for a certain element is 1.94 Angstroms. What is the element?

5b) F+T 1-21a (part a only)