 goes to
goes to
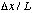 ,
independent of x., no matter if
,
independent of x., no matter if
 is big or small. (which is precisely the classical expectation.)
is big or small. (which is precisely the classical expectation.)Issued Wed, Mar 6 Due Wed, Mar 13
Required reading: through F+T 3.10 (Beiser: through 5.7)
1 F+T 3-7
2 F+T 3-9
3. F+T 3-10
In addition: 3c) Find the expectation value <x>
(Hint: Do you really have to do any integration at all?)
4a) In class, I made a handwavy defense of the correspondence principle: namely, that as n -> infinity, the quantum particle-in-a-box gives the same results as a classical particle-in-a-box.
Sharpen this up, by showing that as n -> infinity, the probability of
finding a quantum particle (in a box of size L) between the positions
 goes to
goes to
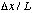 ,
independent of x., no matter if
,
independent of x., no matter if
 is big or small. (which is precisely the classical expectation.)
is big or small. (which is precisely the classical expectation.)
b) An important property of eigenfunctions
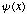 of a system is that they are orthogonal to one another, i.e.
of a system is that they are orthogonal to one another, i.e.
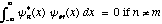 .
(Here,
.
(Here,
 is the wavefunction correesponding to the nth energy eigenvalue)
is the wavefunction correesponding to the nth energy eigenvalue)
Verify this orthogonality relation, for the specific case of the eigenfunctions of a particle in a one-dimensional box.
5a) A particle in a box that runs from 0 to L should have
 by symmetry. Verify that this is correct no matter what n is. Then,
calculate
by symmetry. Verify that this is correct no matter what n is. Then,
calculate
 for the nth wavefunction.
for the nth wavefunction.
b) Show that in general, given some distribution of positions x,
 .
(This quantity represents the deviation from the average, and can be
used as a more rigorous definitition of what we mean by the uncertainty in the
position, or
.
(This quantity represents the deviation from the average, and can be
used as a more rigorous definitition of what we mean by the uncertainty in the
position, or
 .
.
c) Combine a and b, to find the uncertainty in the position of a particle in a box of size L, when n=1. What is the limit as n-> infinity?