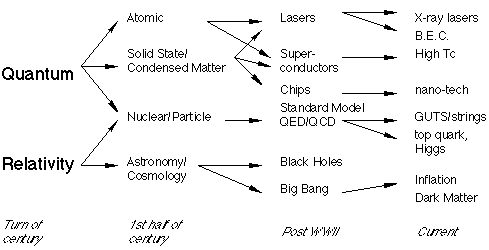
What do we mean by "modern physics"? Here's my own "cartoony" sketch with some topics one might call modern - (of course, other people may disagree with my choices and organization here!)
and on and on, of course! There's LOTS more "modern physics" out there than I can put on this little table. Physics 2170 can thus go many different ways. (E.g., Physics 2130 is a similar course, but with a more superficial survey of the first 2 or 3 columns of that table)
This course will focus on motivating and setting down the foundations of quantum mechanics.
Despite the course title, much of 2170 is about 90 year old physics! It's "modern" with respect to Newtonian/Maxwellian/Thermo of 1110, 1120. And, it is the basis and necessary building block for all the good stuff at the right side of my "cartoon".
We'll skip most of relativity - you'll learn it in both advanced mechanics, and E+M, if you continue on in physics. It is important, but in some ways much more limited in its applications than Q.M. Also, one can pretty well use relativity knowing only a couple of key equations (even if some deeper understanding is missing) But one cannot use quantum mechanics like this! So, it's worth our while to pay most of our attention to developing intuition/foundations/motivations of Quantum Mechanics this semester.
Quantum mechanics is very odd, and having intuition about it is kind of like having intuition about Swahili slang. It's impossible until you've learned not only a new language, but also immersed yourself in a different culture - in our case, the culture of the very small!
We will begin with some history, and learn about experiments that forced us to see the world quantum mechanically. Hopefully, along the way, we will lose some deep-seated intuitions about waves and particles and determinism and predictability, and gain new "quantum" ones. If it seems a bit strange and alien, just grit your teeth and accept experimental facts. That's the nature of modern physics - we can't always completely explain (or understand) why, but at least we want to be able to describe HOW things work!
(186000 miles/sec. It's not just a good idea. It's the law...)
What is quantum mechanics?
We'll be spending much of this semester just beginning to answer this question! It is the basis for almost all of physics, not just the microscopic. But it manifests itself in systems involving "actions" smaller than a special constant of nature, Planck's constant (about 6.6*10^-34 Joule-sec) Systems with large #'s of particles, or large size, are still quantum mechanical, but an approximate description (which is in fact fantastically accurate) is the Classical Limit, i.e. physics you learned in 1110 and 1120. This approximation is NO GOOD for very small systems - there, variables which you are used to thinking of as continuous (like energy) are not. They are discrete, effectively jumping from value to value. They are quantized in steps, hence the name. In the everyday world, these steps are too tiny to notice, but they're still there.
Occasionally, QM can't be ignored even for macroscopic systems (e.g. superconductors, lasers, quantum radiation from black holes, etc.)
Quantum mechanics works beautifully, has been tested and confirmed experimentally in countless ways, and is the basis for most of modern physics, and most of the high technology we see around us. There are some difficult issues involving the philosophy and interpretation of QM (What IS the wave function? What does it mean? Is our world fundamentally, intrinsically indeterminate? How can that be?) But, for the most part, we will take a practical, "physicist's" approach, and try to understand as much as we can along the way. We will mostly learn the "what's" and "how's", if not always the "why's".
Prerequisites for this course: Physics 1110 and 1120 are mandatory.
2140 is important (but if you take it concurrently you may be o.k. - talk to me) . Calculus I and II and some (any) exposure to differential equations are important. But, I'll try to teach what you need to solve QM's primary equation, Schrodinger's equation. Some linear algebra may help you, but again, if you're willing to work a bit to catch up, we won't really use much of it. The most important prereq's are the same ones for every physics class - enthusiasm and curiosity!
Some other comments on math prereq's:
You should be able to differentiate ANY ordinary function.
You should be able to integrate powers, exponentials, trigs.
You should know basic trig identities
(e.g, cos(a+b)=cos a cos b - sin a sin b,
,
etc.)
You should know about complex numbers
(e.g.
, etc...)
You should know some simple power series:
(e.g.
, etc...)
You should know the solution to 2nd order ODE's with constant coefficients
(A y'' + B y' + C y = 0, where y=y(x), A,B,C are constants)
We will be working through the beginning of French and Taylor (F+T) (about the first third), with some side tracks and additional (later) material. But we will begin with some material from Beiser, and throughout this course will parallel much of the first half of Beiser (except relativity) Beiser is bit "easier", so if you're confused, it may help clarify what we're doing!
The first topic of this course in not really so well covered in F+T, they sort of assume it, so you will be working from class notes for the first few lectures. (Beiser Ch. 2 covers this material well) After this, though, we'll follow F+T pretty much straight through...
Here's a summary of the most important units and constants we'll use:
1 eV = 1 electron volt = K.E. acquired by electron accelerated through a potential of 1 Volt:
1 ev = 1.602*10^-19 J = 1.602 * 10^-12 erg (unit of energy)
1 A = 1 Angstrom = 10^-10 m = 10^-8 cm (unit of length)
1 F = 1 Fermi = 1 femtometer = 10^-15 m = 10^-13 cm (unit of length)
1 T = 1 Tesla = 10^4 gauss (MKS unit of magnetic field, gauss is cgs)
m_e = electron mass = 0.511 MeV = 8.19 *10^-14 J = 8.19*10^-7 erg
(Note: the last two are energies on the rhs, but the lhs is a mass!! We are sneakily assuming the formula E=mc^2, so I multiplied t he electron mass by c^2 to get the right side) Of course,
c = speed of light = 3*10^8 m/s = 3*10^10 cm/s
More on units:
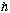= "h-bar" = Planck's constant/(2 Pi) = h /(2 Pi)
= 6.626*10^-34 J sec/(2 Pi) = 1.054*10^-34 J sec
c (= hbar c)
has units of [Joule meter] = [energy length],
c = hbar c
= 200 MeV fm = 2000 ev Angstroms. (Handy to remember!)
Charge of an electron, e = 1.602*10^-19 C (MKS) = 4.803 *10^-10 esu (cgs)
I'll try to stick to cgs units when dealing with E+M, so there are no
's,
and for example
(units on that last equation are
[dynes] = [esu * statvolts/cm] + [esu * (cm/sec) * gauss / (cm/sec)]
Note that e^2/r is an energy (potential energy of two electrons, r apart!)
so [e^2] = [energy * length] = [
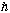c]
* (some number)
In cgs units, e^2/(
c)
= 1/137 =
,
the fine structure constant
Here is the Next lecture
Back to the list of lectures