
Now, one of relativity's basic equations is the connection between energy,
mass, and momentum. Non-relativistically, the formula is (neglecting
potentials):

Relativistically, it becomes:
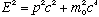
(Check: If p is small:

the non-relativistic result comes out as a limit of the relativistic formula!)
In the energy-momentum formula, m_0 is the rest mass. Photons, being massless,
give E^2 = p^2 c^2, or E=pc. Now, we can relate the wavelength of a photon to
its energy:
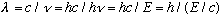
Combining this with E=pc gives
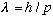 .
.
I just derived this for a photon- but this equation is very significant, and will turn out to be relevant far beyond how we just derived it.
We can do the kinematics of Compton scattering, given only the one relativity formula above:
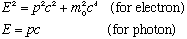
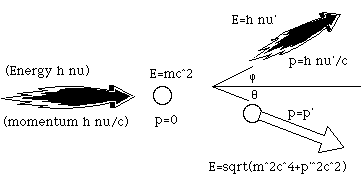

Now rewrite,. replacing frequencies for wavelengths (nu = c/lambda) giving

This last line was Compton's prediction. Lambda (wavelength) of the photon changes when the photon scatters through an angle phi. The prediction comes purely from imagining the photon is a little (relativistic) particle, and nothing else. This prediction was verified 1919-1923, providing yet another measure of h.
(Duane tried this experiment, at Harvard, and he got the classical result! (i.e. no observed shift in wavelength) Young Compton had to fight at the big physics meeting that year, against the senior and respected Duane. Compton later went to Harvard to visit with Duane, and helped find the problem with Duane's experiment)
Things to note:
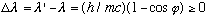
So, the wavelength always gets longer (i.e, the photon always loses energy, just like our billiard ball)
Delta lambda is independent of lambda.
The scale is set by h/mc, which is called the "Compton wavelength" of the electron:

(which is very small)
Delta lambda is so small, it's hard to see experimentally unless lambda is already quite small (i.e., X-rays)
Compton scattering off of electrons is the main way the X-rays lose their energy in matter.


Q: Why do we still see a peak at lambda_0, the original wavelength, along with the shifted one?
A: Some electrons are tightly bound. I assumed free electrons in my calculation. If they're bound, the whole atom recoils, so the effective mass m is not m_e, but 1000's of times bigger, so Delta lambda is 1000's of times less!
Why are there tails? Why not just spikes at the predicted wavelengths? I assumed the electron was a rest. But, if it moves, its initial energy and momentum will spread out the final X-ray energy. Also, the photon could scatter twice or more...
The Compton effect really shows the dual nature of light. The detection of the X-rays is done by Bragg scattering, a classical interference effect which requires a wavelike nature for light!
Example: X-rays have wavelength of 10 pm. What is the maximum wavelength found in the scattered X-rays?

(a 50% increase)
Note: Visible light has lambda around 5 micrometers, so the maximum wavelength would be 5*10^-6 + 5*10^-12 = 5.000005 * 10^-6, which is why Compton scattering is so hard to detect with visible light.
Back to the list of lectures