Vibrations of diatomic molecules.
Molecules have some equilibrium separation of the constituent atoms (couple of Angstroms), and behave like they're hooked by a spring.
Note that the classical H.O. we've been dealing with looks like this:
Here F=-C(x-x0), and
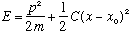
But for a diatomic molecule, there's no "fixed wall", so it looks like:
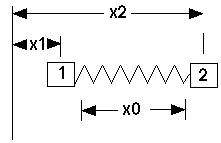
This is a bit different, especially when m1 differs from m2. Here:
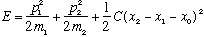
Now move to the center of mass position,
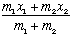
This is the location of the center of mass. If that starts at rest, the objects can oscillate all they want, but the center of mass will remain at rest!
In the CM frame, p1=-p2 == p (total momentum=0), and
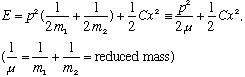
where
The resulting energy equation looks JUST like the classical harmonic oscillator, with a single mass, given by the reduced mass! So, the two particle system is formally equivalent to a single particle with reduced mass. If this represents a molecule, then we are going to have to solve the Schrodinger equation
The wave function here represents the effective one body wave function,
i.e.
tells us the probability that the molecular separation will be x.
But we've done this problem!
So, go and measure the energy spectrum for molecular systems. E.g., look at CO,
and Cl2. Note that the reduced mass of these molecules is easy to compute:
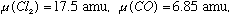
So if we can measure the energy spacing between lines, we can then deduce the spring constant in these molecules!
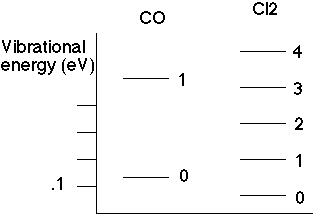
From the data, one gets e.g. C(Cl2) is about 320 N/m, while C(CO) is about 1860 N/m. French and Taylor have many such force constants, ranging typically from 300-2000 N/m, which is in fact a pretty "typical" force constant. (It's the same as for atoms in a crystal, and even ordinary springs like you might find in the lab. In English units, 100 N/m is about 1/2 lb/inch) Car shocks are rather stiff, they might be around 10000 N/m.
We can also work out the zero point energy.
For CO, we have a reduced mass of 6.85 amu = 6.85 * 1.66 * 10^(-27) kg. I claimed the spring constant was about 1860 N/m. Hence,
This is an infrared type energy. Note that at 300K, kT = 0.03 eV = 1/40 eV, so at room temperature CO will be in its ground state. There is not enough thermal energy to excite even the very first vibrational mode!
There is a rule, called a "selection rule", which says that for radiation or
absorption of a photon in a harmonic oscillator, the change in n can
only be +/-1. That is, harmonic oscillators are very happy absorbing photons of
energy
,
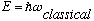but that's it! They do not like to absorb or emit, say, twice this. Only
the classical oscillator frequency gets absorbed or emitted. This was Planck's
postulate to derive the blackbody system! It is now coming out as a
consequence of quantum mechanics (although we won't prove the selection rule in
2170)
Comment on zero point energy. Note that the ground state energy is
.
But, you might ask, how can you ever tell its there? Since all you ever measure
is transitions between levels, how can you tell if the bottom level has zero
energy or not? Liquid He doesn't freeze - there's a hint! There are in fact
many ways to "observe" the zero point energy. More on this next time!!
Sidetrack:
Before we go on to the next topic (1-D S.E. with positive energies, i.e. unbound states), let's try to understand how Mathematica might be weaving its magic in NDSolve. How can a computer solve Schrodinger's equation numerically? It's obviously of enormous practical value! First, we convert to a dimensionless form of the S.E., as we've done before (in the homework, e.g.) That way, we can compute with pure numbers, which is generally easier. Convert
into
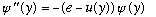
Here, y=x/L, where L is some natural distance scale in the problem, and
e=E/(natural energy). For a square well, e=E/V0, for the harmonic oscillator,
,
etc.
For the harmonic oscillator, we did this before, and got
,
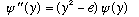the potential function u(y) is just y^2, the "universal" (unitless) quadratic
potential.
Bottom line, no matter what your potential, you can always write the SE in a unitless form. Now, to solve numerically, we must convert the differential equation to a difference equation. Imagine that we only care about the wave function at discrete y points:
By making Delta y -> 0, we have found the wave function (almost) everywhere, which is surely good enough!
Now look carefully at the y axis:
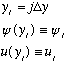
Careful! j is no longer the "quantum number" label used before. We are only talking about one particular wavefunction here! j now labels the particular point that we're looking at! What is the derivative of the wave function at the point half way between point j and j+1?
By convention, we can call this
,
because we really ONLY want to talk about quantities evaluated on the grid
points, not between them.
Next, what is the second derivative of the wave function at the jth pt?
I can rewrite this in the following way, using the S.E. for the 2nd deriv,
:
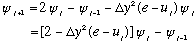
What does this mean? If you tell me
and
(i.e. the value of the wave function at any two adjacent points), I can now
compute the value at the next point over. And then I can use THAT one to
compute the next one after that, and so on! Also, I can work my way
left, by writing
Simply picking 2 initial adjacent values of the wave function gives me
everything! These 2 initial points are the boundary condition.
Alternatively, I can give the wave function and its derivative at one
point, because
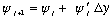
In MMA hw's, we've often used
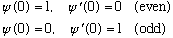
So with this new numerical technique, we'd set
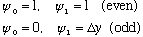
Just like with MMA, we don't know what value of e to use. We must try out
different values, until the wave function goes to zero at large j. (Also, if
the potential is not symmetric, and stays finite, then you pick
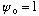arbitrarily, and then you must vary both
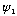and e. Only one magic combo will give you a solution going to 0 at infinity!
This is clearly more painful)
MMA's NDSolve is using rather more efficient and accurate tricks than this, but the fundamental idea is the same.
Here is the Next lecture
Back to the list of lectures