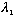(
has nothing to do with wavelength, it's just a linear charge density!)
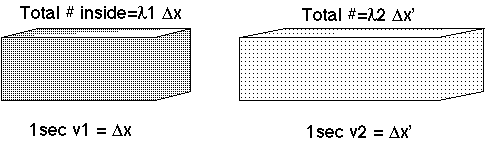
Formally, if you have a charge density
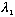with velocity v1, then conservation of current says current=
.
Here, our analog of "charge density" is probability density, the square of the wave function. After all, (charge/particle)*probability density = charge density. (they're proportional)
So, we should expect that the probability flow depends not just
on the square of the wave function (or
),
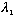but also on the velocity! In particular, the transmitted fraction should be
outgoing "current"/incoming "current" =
,
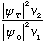and thus we expect T should be given by
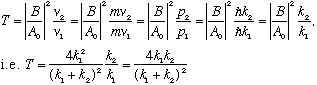
(which is indeed 1-R)
So everything is really ok. This is all pointing to the idea of probability currents, a concept very fundamental and important in quantum mechanics. But we leave this now as an interesting "temporary dead end", and return to questions of transmission and transmission.
The (unbound) square well potential.
Consider particles, again coming in from the left, but now encountering a square well.
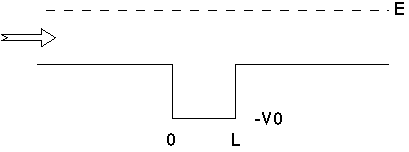
This is different from our previous square well case, only in that particles are not bound. (e.g., high energy electrons running right through a foil) Classically, the particles speed up while in the well, pass through, and slow down to their original speed on the far side.
Quantum => some will "bounce"! In fact, any time particles encounter a sudden change in potential (up, like in the last problem, or down, like here), they can bounce! So, you might expect:
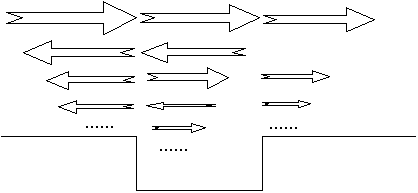
It's painful to think of partial transmission and partial reflection at both walls, because we'd have to add up an infinite sum. But, in the steady state, we just play the usual game. Solve the SE, and satisfy the B.C.'s!
In regions I and III,
.
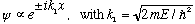except in region III, there should only be +ikx in the exponent, because the negative sign corresponds to a wave moving to the left, coming from infinity, and that doesn't make any sense.
In region II,
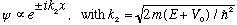
Putting this together:
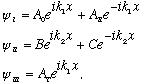
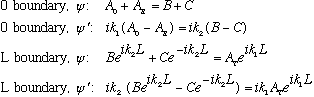
We have 4 equations in 5 unknowns (much like before), and we must find Ar/A0, At/A0, etc. (We really don't care what A0 is, after all, so we don't NEED the 5th equation, which is just normalization, as usual)
This is a slightly nasty piece of algebra, though not impossibly so. F+T do it (p. 380). From the 2nd pair of equations, it's easy to get both B and C as functions of At. (e.g., multiply equation 3 by ik2, add it to #4, and you eliminate C, giving
,
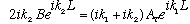i.e. giving B in terms of At. Similarly, you can get C in terms of At.
Also, you can see that (ik1 times #1+#2) will eliminate Ar, so plugging in what you just got for B, and C, in terms of At, means you can find A0 in terms of At, which you then invert to get At/A0, which is what we're after. (Phew!)
We know that
,
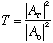with no "velocity factors", because the velocity is the same in regions I and
III, and solving the algebra gives
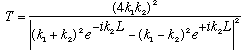
and of course, R=1-T by "conservation of probability", which saves us some minor amount of grief. (Once we know T, we know R, we don't have to solve for it directly)
This formula for T is a bit ugly (i.e., not very transparent) But we can see right away what happens in some interesting limits.
1) k1=k2. (This means there's no well at all! i.e. V0=0)
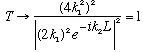
Good thing too!
2) k1 close to k2 (i.e., a weak well, i.e. V0 << E)
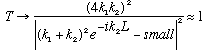
(Nothing odd happens, we mostly transmit, as expected)
3) k1 << k2 (i.e. a deep well, i.e V0 >> E)
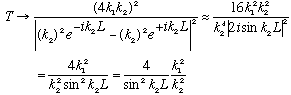
This means that, generally, since k1 << k2, T -> 0, so deep wells reflect everything! This is very non-classical. Remember that for marbles, a deep well speeds you up for awhile, but NEVER reflects. We can also notice that
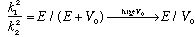
So T is small, but it does increase linearly with energy, for a fixed potential. This is clearly something to test quantitatively in the lab.
4) A cool sub-case of the above happens if (k2)L = n Pi! In that case, it looks like trouble, because the sin^2 in the denominator goes to zero, i.e. T -> infinity! (Impossible, T=1 is the biggest it can be!)
But we made some approximations in getting to our final result, we better go back to the start and do it right:
(We'll do this next time)
Here is the Next lecture
Back to the list of lectures