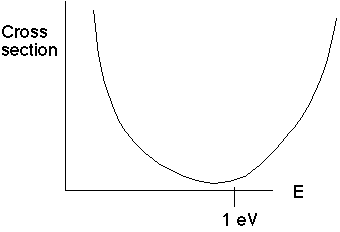
This phenomenon was first seen experimentally in the 1920's. Ramsauer and Townsend (independently) beamed electrons at atoms.
They looked at the relative cross section (which is the "scattering likelihood), as a function of the electron beam energy. They found that there was a special energy with a very low likelihood of scattering. (i.e. high transmission)
Of course, atoms are 3D, but imagine they're sort of like a little box, with L=2R, and so from our above calculation, we expect T=1 when
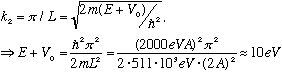
We would expect V0 to be something on the order of a few eV (up to 13.6, say), so it's reasonable to see the first minimum at E=1 eV (so E+V=10). This tells us what the effective "well depth" of an atom is. Atoms don't in fact usually look exactly like square wells, but noble gasses have tightly bound electrons, so the potential change is quite sudden.
A second minimum would give us E+V0=40 eV, i.e. E=31 eV. In this case, the V0 <<E limit comes in, and T=1 just because the well isn't very significant, so the next minim(a) are much less dramatic.
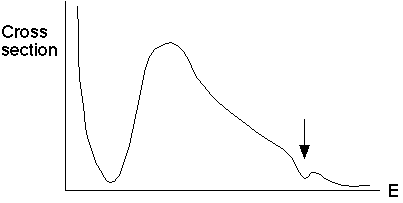
(i.e., they're not so noticeable because the cross section curve is dropping anyway)
Finally, we do one more barrier example. This one is surely the most remarkable of all! It's an upside down box.
Unlike our very first example (which simply had a step up), in this one after some distance, L, the barrier drops again to 0.
This might, e.g. be an insulating gap between conductors.
For E(hi), it's nothing different from the previous case. Just let V0 be negative, and all our formulas go through. Nothing especially new happens in this case. For E(lo), it's a slightly different story. Classically, of course, E(lo)<V0, so the particle bounces backwards. Even if V is rounded, if E<V, a classical particle bounces 100% of the time. The quantum case gives
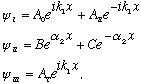
where
.
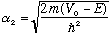Once again, we will have 4 equations in 5 unknowns, and once again we really are only interested in T and R, so we don't need the "5th" amplitude (A0). It's VERY similar algebra to what we did for the square well, except in region II we have real exponentials rather than imaginary ones.
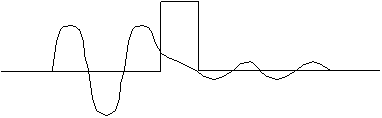
The solution gives mostly dying exponential in that region.
On the right side, it has the same wavelength as on the left, just a smaller amplitude. The most interesting quantity, again, is T=|At|^2/|A0|^2. This time, the formula is
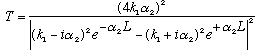
(It's exactly the same as before, just replace (i k2) -> alpha2!!)
Realize what this is: transmission through a rigid barrier! It's also called tunneling.
Again, let's look at some limits:
1)
.
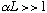This limit can either mean L is big, or (V-E) is big, in either case the
barrier is big in the sense of being tall or wide, and
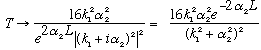
Note, f.y.i., the "denominator" algebra went like this:
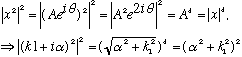
If you now divide by k1^4 upstairs and downstairs, you get
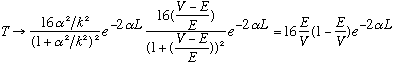
Since 0 <= E/V <1 (we're considering the case that E is below the top of the barrier), then E/V(1-E/V) is also between 0 and 1, and in general is some small but not infinitesimal number. The exponential, on the other hand, is generally wee! It dominates, and makes T small, as you'd intuitively expect.
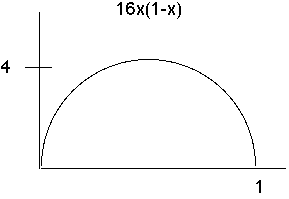
In fact, the coefficient 16(E/V)(1-E/V) is reasonably constant, rather independent of
E and V
(see the picture of 16x(1-x) vs x,
with x=E/V)
so we often approximate
.
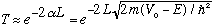It's small, but it's not zero. (So, if I'm sitting on the table, there really is a small chance that I can "tunnel" through to the other side)
Example: Electrons with E=3 eV hit a barrier V0=10 eV (a typical work function of a metal), with L=4 A. This might be a thin oxide gap in a conductor. What's the probability of an electron "popping through" the barrier?
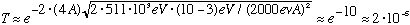
This is small, but it can be important! If you put in all the proper factors, you're correct to within a factor of three. (Real T is bigger)
Note that doubling the width SQUARES the answer (=> 4*10^-10)
So, tunneling probability is very sensitive to the size of the barrier.
The Scanning Tunneling Microscope is based on this idea. (So is Field Emission Photography).
By the way, tunneling does occur classically, but it's again a wave phenomenon.
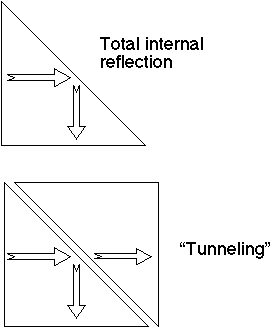
When you have light hitting a surface you get total internal reflection. But if you put another surface nearby, you get tunneling.
Here is the Next lecture
Back to the list of lectures