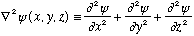 .
.(F+T CH. 5, Beiser Ch. 6)
The real world is 3-D, and this adds both some complication and some new richness to Schrodinger's equation. In some ways, 3-D quantum will be very familiar, but there are also things (like rotation!) that have no clear 1-D analogy. The S.E. generalized to 3-D as we've mentioned before: Instead of the term with d^2 psi/dx^2, we have
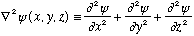 .
.
This is really just coming from the fact that p^2 =p_x^2+p_y^2+p_z^2.
So, the new 3-D S.E. looks like
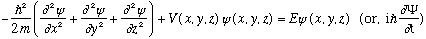
(The latter gives the full time DEpendent S.E., and just as we've been doing in 1-D, we're going to focus on "stationary states", i.e. those with a unique energy, which means
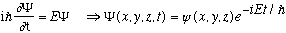
So, that time dependence is just a common factor in ever term, and we cancel it and henceforth ignore it.
(Note: If the potential depends on time, or you want to consider e.g. an initial state that doesn't have a unique, well defined energy, like a particle sloshing back and forth between wells or something, then you have to go back and include the time dependence. Quantum mechanics treats time dependent problems just fine, if you need to worry about it. We just won't get to treat these in 2170!)
So now we have a time independent S.E. which is no longer an ordinary diff eq., like it's been all semester up to now - it's a partial differential equation. If we have a hope of solving it analytically, it'll succumb to separation of variables, a technique we learned at the end of 2140. This is not guaranteed to work, but you can always try!
This technique boils down to the hope that a separated, or factorized solution will work, i.e. you try
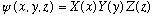
Since the S.E. is linear, a constant times psi is still a solution, and also if two different solutions, psi1 and psi2 work, then (a psi1 + b psi2) also works. So, our factorized solution may turn out to be too simple, but adding up linear combinations may do the trick!
First example: An infinite square well. But now, in 3-D! So, this looks like a box with rigid walls.

The particle is free to roam around inside (V=0), but it bounces off of the walls elastically. (V-> Infinity at the edges) Note that the "infinite well" is infinite in potential at the walls, but it's still finite in extent. It used to run from x=0 to L in 1-D. Now, we might as well generalize and let it run from x=0 to a, y=0 to b, and z=0 to c.
What are our boundary conditions?
Clearly, the wave function must go to zero at x=0 and x=a, because the particle can't be found at, or outside, the box. This is the same condition we had for the 1-D box. Now, we also add that psi goes to zero at y=0, y=b, z=0, and z=c, as well as everywhere outside.
What is our differential equation? We take the S.E., plug in our separated guess, psi=X Y Z, and then we divide both sides of the resulting equation by psi. Also, we note that when taking partial derivatives with respect to x (for example), any function (like Y(y) and Z(z)) which is independent of x just moves through the derivative like it was a constant. So, when we divide through by psi, those terms will simply cancel out. (We did this many times in physics 2140!)
The result is that inside the box, where V=0, we get
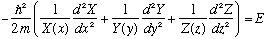
Note that the first term is a function of x only, the second term of y only, the third of z only, and the RHS is a constant, independent of all variables. This cannot be true! A function of x can't equal a function of y! It can't, unless the function is simply a constant! This means that each of those three terms in the equation must separately be pure constants. Let us give the three constants names, e.g. the constant for the x equation will be called E_x, etc. It's just a name. The resulting three equations are all ordinary differential equations, because they each depend only on the one variable. They look like the following:
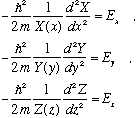
and now E=E_x+E_y+E_z. So, there are 3 constants in this problem, and once we know all three, then the real total energy is determined. Now look at the X equation. We can rewrite it as
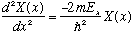
We know and love this ordinary differential equation! By now, we can just write down the solution by inspection:
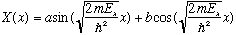
The boundary condition at x=0 says X(0)=0, i.e. b=0.
The boundary condition at x=a says X(a)=0, which then forces the argument of the sin, at x=0, to be an integer number of Pi. Let's call that integer n_x, so we get

and exactly similarly for y, and z. Putting it together, we get

A is, as usual, the normalization constant. You would figure out what it is by arguing that the probability of find the particle SOMEwhere is 1, i.e.

Since each of the separated wave functions looked just like a simple old 1-D equation, the total energy is just the simple sum of 3 independent 1-D well energies! (Life is not always so simple, as we shall see! The square box is a particularly friendly case, that's why we start with it)
Electrons in a tiny chunk of metal might be described reasonably well like this.
There are now three "quantum numbers" required to describe any given stationary state, nx, ny, nz. (In 1-D, we only needed one number, n) Once you know those 3 numbers, the energy and wave function (and hence anything you ever wanted to know about the particle) are fully determined.
The ground state is nx=ny=nz=1. (Note that NONE of the quantum numbers can be 0, because sin(0)=0, and so this would make the whole wave function be 0 everywhere, which means no particle!)
if a=b=c, the first excited state is not unique! For example, if
nx=2, ny=1, nz=1, or nx=1, ny=2, nz=1, or nx=1, ny=1, nz=2,
the energy will be exactly the same, but the wavefunction is NOT the same! This is called "degeneracy", because the energy levels are degenerate, they're at exactly the same place. It arises from an underlying symmetry (namely, that a=b=c, i.e. it's a nice cubic box). If you break the symmetry (let a, b, and c differ slightly) then you also break the degeneracy, the 3 energies are no longer exactly the same.

In nature, many systems are nearly degenerate, but not quite. The tiny splittings tell us LOTS about the underlying physics! Also, you could have "partial degeneracy", if e.g. a=b, but c was different...
Next topic: "Spherically symmetric potentials"
Here is the Next lecture
Back to the list of lectures