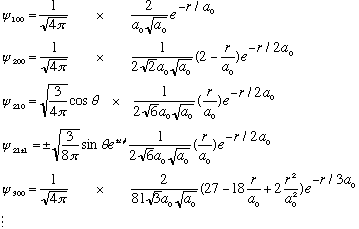
Let's look at some of the hydrogen wave functions, just to get a little better feel for them.
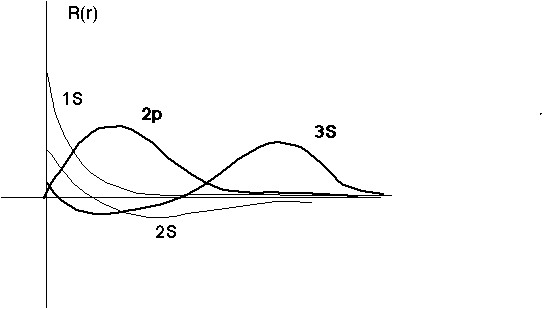
The 2p has no node (except at 0), while the 2s does have a node. The 2p is certainly not the same as 1s, but in a sense is kind of like a "ground state". (In the energy level diagram, it's the first state in the "tower" of possible energies for l=1) The 3d is like this too... The 2p goes to 0 at the origin (unlike the 1s and 2s) because it has angular momentum, so there's an infinite barrier at the origin, so it must vanish there.
Squaring the wave function, and multiplying by r^2, tells you what you'll really be integrating over r to find expectation values:
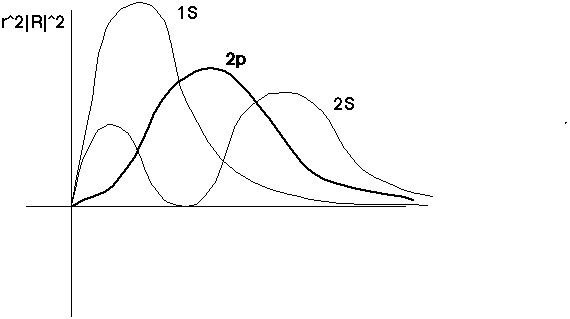
The 2p has no nodes (the 2s does have one). The 2s extends out farther than the 1s (because the exponent is slightly smaller)
Now we look at the angular (theta) dependence. (The phi dependence is pretty trivial, and completely uninteresting physically, because when you square Phi(phi) you always just get 1) I make a polar plot of Theta(theta), and |Theta(theta)|^2:
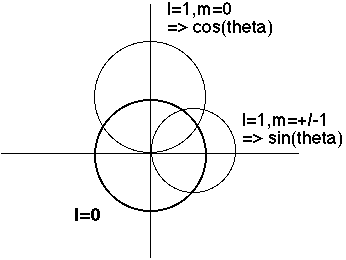
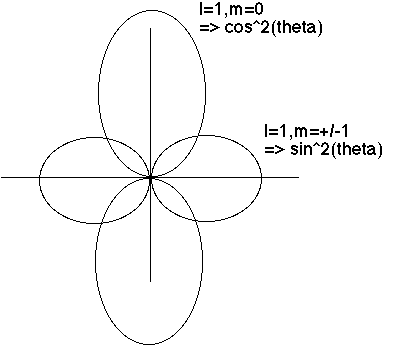
One can even superpose both the r and theta dependence, Beiser (6.10) does a nice job of this.
E.g., l=0 => Spherically symmetric (no angular momentum)
Always an exponential decay radially.
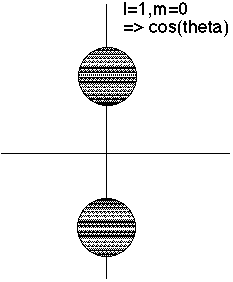
l=1 has an r^2 factor, which cuts out strength at the origin.
m=0 goes like cos^2(theta), so biggest at theta=0 or Pi (North and south poles)
See Beiser for much more realistic versions!!
This sort of pattern has a lot to do with atomic/molecular bonding, and the ways that adjacent atoms interact, of course.
Consider l=1, m=+/-1, n=2. This is a donut, and the most probably distance (the maximum value of r^2 R(2p)^2 is at 2^2 a0. (This is just what Bohr said!)
Similarly, l=2, m=+/-2, n=3 is again a donut, and the most probably distance is at 3^2 a0.
In general, for any given n, if you look at the maximum allowed angular momentum (l=n-1), then the most probable distance is at
the Bohr prediction, n^2 a0. This is the most "circular" orbit, so it's reasonable that it would be the closest to Bohr.
As I mentioned before, <1/r> will always give you (1/n^2 a0), no matter what l is)
Also, given this maximum l, the maximum m=l will always give you a donut. It's the most "classical" orbit you can hope for. (1s,m=0, 2p,m=+/-1, 3d,m=+/-2, etc)
This concludes our preliminary look at the 3-D S.E, and ends the major portions of the syllabus.
Here is the Next lecture
Back to the list of lectures