Last time, we were studying the example of a block on a ramp:
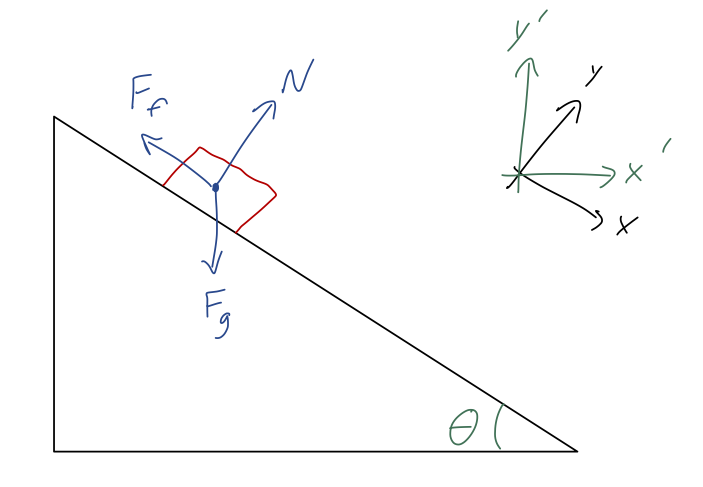
and ended on having found the equations of motion in the primed coordinates,
\[ \begin{aligned} \ddot{x}' = g \cos \theta (\sin \theta - \mu \cos \theta) \\ \ddot{y}' = -g \sin \theta (\sin \theta - \mu \cos \theta). \end{aligned} \]
Now let's keep going and find the solutions. The good news is that even though these still don't look so nice, everything on the right-hand side of both equations is constant, so to solve for the motion, all we have to do is integrate twice, for example:
\[ \begin{aligned} \dot{x}'(t) = v_{x,0} + \int_0^{t} dt' \ddot{x}'(t') = v_{x',0} + gt \cos \theta (\sin \theta - \mu \cos \theta) \\ x'(t) = \int_0^t dt' \dot{x}'(t') = x'_0 + v_{x',0} t + \frac{1}{2} gt^2 \cos \theta (\sin \theta - \mu \cos \theta) \end{aligned} \]
and similarly,
\[ \begin{aligned} y'(t) = y'_0 + v_{y',0} t -\frac{1}{2} gt^2 \sin \theta (\sin \theta - \mu \cos \theta). \end{aligned} \]
If we assume starting from rest, then \( v_{x',0}, v_{y',0} \) are set to zero; we'll do that from here forward, although our solution can handle a starting speed as well. (One tricky little detail: we've assumed that the block stays on the surface of the ramp for the whole motion. This restricts the direction of the initial velocity, which means we can't just pick any arbitrary \( v_{x',0} \) and \( v_{y',0} \).)
Let's check some limits! (I leave it to you to verify that the units all make sense.) If \( \theta \rightarrow 90^\circ \), then the ramp becomes completely vertical, so the motion should only be in the \( y' \) direction, and it should just be freefall. At \( 90^\circ \) we have \( \cos \theta = 0 \) and \( \sin \theta = 1 \), so
\[ \begin{aligned} x'(t) \xrightarrow{\theta = 90^\circ} x_0' + \frac{1}{2} gt^2 (0) (1 - 0\mu) = x_0' \\ y'(t) \xrightarrow{\theta = 90^\circ} y_0' - \frac{1}{2} gt^2 (1) (1 - 0\mu) = y_0' - \frac{1}{2} gt^2 \end{aligned} \]
so indeed, we have freefall in the \( y' \) direction and no motion in the \( x' \) direction.
How about the opposite limit, \( \theta \rightarrow 0^\circ \)? Since the motion is entirely caused by gravity, what we expect to find is that as the ramp becomes completely flat, all motion stops. Plugging in again, we find this time that
\[ \begin{aligned} x'(t) \xrightarrow{\theta = 0^\circ} x_0' + \frac{1}{2} gt^2 (1) (0 - 1\mu) = x_0' - \frac{1}{2} \mu gt^2 \\ y'(t) \xrightarrow{\theta = 0^\circ} y_0' - \frac{1}{2} gt^2 (0) (0 - 1\mu) = y_0' \end{aligned} \]
The \( y'(t) \) result is fine, but our block will apparently start sliding backwards in the \( x' \) direction if the ramp is laid flat! What went wrong with our calculation?! (Think about it yourself, before you continue reading...)
In fact, our calculation above is just fine. The problem that was revealed when \( \theta \rightarrow 0^\circ \) has to do with our starting assumptions. In particular, we assumed a single coefficient of friction \( \mu \). Since our block is in motion, this must be the coefficient of kinetic friction, \( \mu_k \). However, we know that there is also a coefficent of static friction \( \mu_s \) that must be overcome if the block is starting at rest,
\[ \begin{aligned} F_{f,s} \leq \mu_s mg \cos \theta, \end{aligned} \]
which will keep the block from moving (i.e. give zero accelerations) if the other forces are not large enough. We can take the \( x' \)-direction net force and solve:
\[ \begin{aligned} F_{\rm net, x'} = N \sin \theta - F_f \cos \theta = 0 \\ mg \cos \theta \sin \theta = F_f \cos \theta \\ mg \sin \theta \leq \mu_s mg \cos \theta \\ \tan \theta \leq \mu_s \end{aligned} \]
So the full picture is: if the angle \( \theta \) is small enough that \( \tan \theta \leq \mu_s \), then the block just won't move at all. Since generally \( \mu_k \leq \mu_s \), this means that \( \tan \theta \geq \mu_k \) whenever static friction is overcome; this means that the offending term which changed the sign of our \( x' \)-direction motion,
\[ \begin{aligned} (\sin \theta - \mu_k \cos \theta) \geq \sin \theta - \tan \theta \cos \theta \geq 0 \end{aligned} \]
and we don't have any problems with backwards-moving blocks anymore.
One last thing we should do is compare our answer to Taylor's answer, which means we need to change coordinates.
Exercise: Checking against Taylor's example (1.1)
Change coordinates in order to find \( x(t) \) from our results for \( x'(t) \) and \( y'(t) \). (Assume the block starts at the origin and begins at rest.)
This is a nice exercise, because it really drives home the point I started this whole discussion with: to compare our calculation to Taylor, we have to figure out how to put them into the same coordinate system!
Once again, in lecture I'll pause to let you think about this one; if you're reading along after, try it out yourself before you keep going.
To solve this, we start by drawing a couple more triangles:
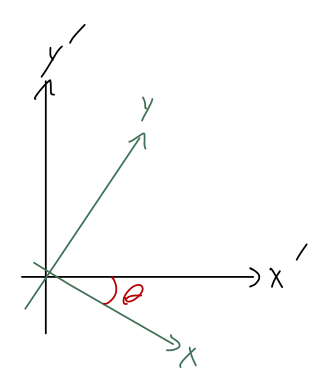
from which we readily see that
\[ \begin{aligned} x = x' \cos \theta - y' \sin \theta \end{aligned} \]
Putting our solutions together, then, we have (starting from rest and the origin as we were told)
\[ \begin{aligned} x(t) = \cos \theta \left(\frac{1}{2} gt^2 \cos \theta (\sin \theta - \mu \cos \theta)\right) - \sin \theta \left( -\frac{1}{2} gt^2 \sin \theta (\sin \theta - \mu \cos \theta) \right) \\ = \frac{1}{2} gt^2 (\sin \theta - \mu \cos \theta) \end{aligned} \]
and if we open up the textbook, we'll find that this matches Taylor's solution exactly.
Reference frames and mechanics
Whenever we do classical mechanics, we have to specify a reference frame. Reference frames are choices of coordinate systems, but because we're dealing with both time AND space, they have an extra complication as compared to fixed coordinates: two frames can be moving relative to one another. Following Taylor, we'll use a script \( \mathcal{S} \) to denote a reference frame. \( \mathcal{S} \) includes a coordinate system, an origin \( \mathcal{O} \), and finally some specification of how \( \mathcal{O} \) is or isn't moving, relative to some physical object or other point of reference.
Our chosen coordinates \( (x', y') \) for the ramp problem are an example of a reference frame \( \mathcal{S}' \); Taylor's rotated coordinates \( (x,y) \) are a different reference frame \( \mathcal{S} \). Both frames are fixed with respect to the ramp, which means there's also no relative motion between \( \mathcal{S} \) and \( \mathcal{S}' \). However, we could come up with a third frame \( \mathcal{S}'' \) with coordinates \( (x'', y'') \), defined by the following relations:
\[ \begin{aligned} x''(t) = x'(t) - ut \\ y''(t) = y'(t) \end{aligned} \]
In other words, the origin of \( \mathcal{S}'' \) is moving horizontally to the right with constant speed \( u \).
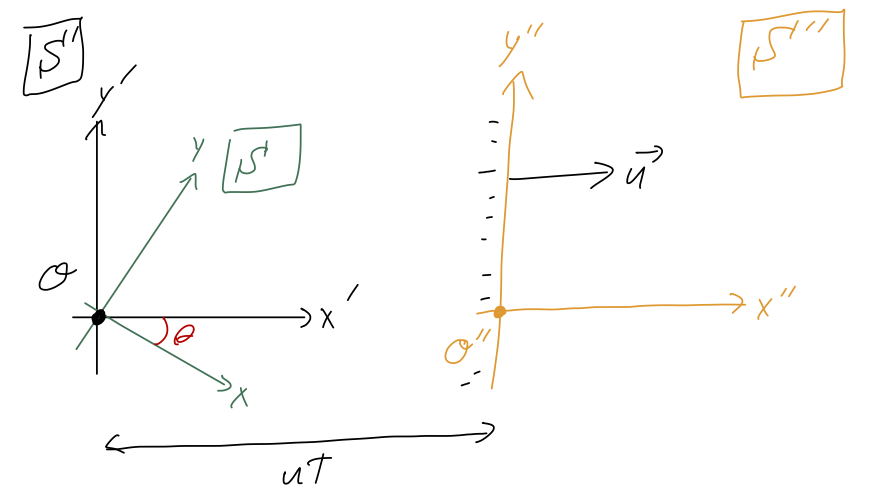
Since we already solved for the motion in \( \mathcal{S}' \), we can just use the coordinate change to find the motion in \( \mathcal{S}'' \):
\[ \begin{aligned} x''(t) = x''_0 + (v_{x',0} - u) t + \frac{1}{2} gt^2 \cos \theta (\sin \theta - \mu \cos \theta) \\ y'(t) = y''_0 + v_{y',0} t -\frac{1}{2} gt^2 \sin \theta (\sin \theta - \mu \cos \theta). \end{aligned} \]
Notice that if our block starts at rest with respect to the ramp, it will appear to be moving to the left with initial speed \( u \) in our moving coordinates.
Just using a change of frame on our solution is always valid; if we have solved the equations of motion in one reference frame, we know the answer in any other frame. However, we have to be careful if we start in a given reference frame and try to apply Newton's laws. If you try it in the \( \mathcal{S}'' \) frame, the forces will all be exactly the same, and you'll find the same answer that we got above. However, consider a different example:
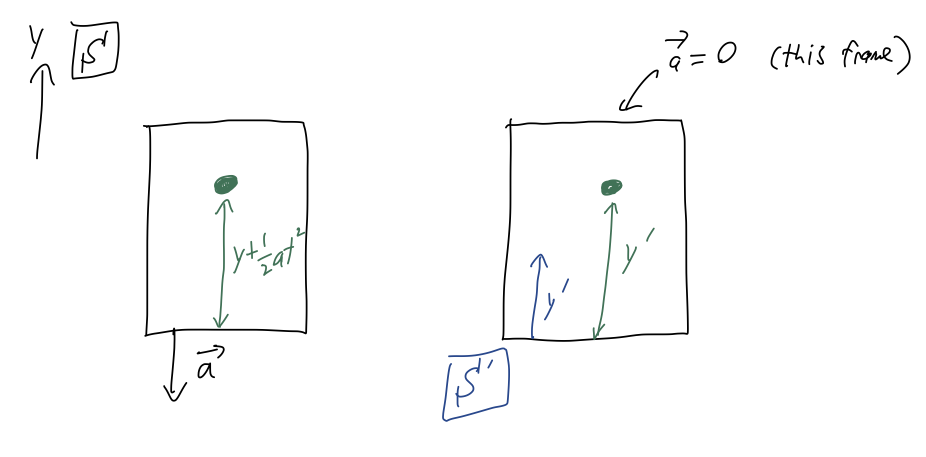
We drop a ball inside an elevator, from initial height \( y_0 \). From the point of view of frame \( \mathcal{S} \), fixed with respect to the ground, the elevator is moving straight down with constant acceleration \( a \). As pictured, we can define a second frame of reference \( \mathcal{S}' \) which is fixed to the elevator (so the point of view of an experimenter riding the elevator, basically.)
Let's work out the motion in frame \( \mathcal{S} \) first. Neglecting air resistance, the only force acting on the ball is gravity:
\[ \begin{aligned} \vec{F}_g = -mg\hat{y} \end{aligned} \]
Using Newton's second law,
\[ \begin{aligned} \vec{F}_{\rm net} = -mg \hat{y} = m\vec{a} = m(\ddot{x} \hat{x} + \ddot{y} \hat{y}) \end{aligned} \]
so nothing happens in the \( \hat{x} \)-direction, but vertically we have a constant acceleration, \( \ddot{y} = -g \). If we drop the ball at rest, integrating twice gives us
\[ \begin{aligned} y(t) = y_0 - \frac{1}{2} gt^2. \end{aligned} \]
So far, we haven't mentioned the elevator at all; it enters in when we ask how far the ball is from the floor of the elevator at any given time. From the diagram, we can see right away that
\[ \begin{aligned} \Delta y(t) = y(t) + \frac{1}{2} at^2 = y_0 + \frac{1}{2} (a-g) t^2. \end{aligned} \]
In particular, notice that if the elevator is also free falling (\( a=g \)), then the ball will appear to be suspended above the floor.
What about the frame \( \mathcal{S}' \)? Well, the only force in the problem is still gravity, so we conclude right away that
\[ \begin{aligned} y'(t) = y'_0 - \frac{1}{2} gt^2. \end{aligned} \]
But \( y'(t) \) is exactly the same thing as \( \Delta y(t) \), the distance from the floor to the ball! But we don't see \( a \) anywhere, and in particular we don't see any possibility for the ball to be suspended in mid-air. This is a contradiction!
Obviously, one of our answers is wrong, and if you remember the fine print on Newton's laws, you may already know the answer: the calculation in \( \mathcal{S}' \) is wrong, because \( \mathcal{S}' \) is an accelerating frame of reference. Accelerating frames are also called non-inertial frames, because the law of inertia (Newton's first law) doesn't hold, and clearly neither does the second law.
The good news is that we're never forced to use a non-inertial frame, because frames of reference are our choice! Our calculation in the frame of an observer outside the elevator is perfectly fine. But it's an important point to be aware of. Unless we specify otherwise, for the rest of the semester we'll work only in inertial frames (i.e. non-accelerated ones where Newton's laws are good.)
There is, in fact, a way to modify Newton's laws so that they will work in an accelerating frame - this involves adding so-called 'fictitious force' terms. (If you've ridden in a fast elevator, you know these forces are something you can easily feel!) But that's a topic for next semester.