Last time, we wrote down formulas for the position \( \vec{R} \) of the center of mass:
\[ \begin{aligned} \vec{R} = \frac{1}{M} \sum_{\alpha=1}^N m_\alpha \vec{r}_\alpha, \\ \vec{R} = \frac{1}{M} \int \vec{r}\ dm = \frac{1}{M} \int \rho(\vec{r}) \vec{r}\ dV. \end{aligned} \]
Before we get into doing integrals, it's a good idea to run through the center of mass calculation for two point masses, which we'll call \( m_1 \) and \( m_2 \). Let's set up our coordinates like this:
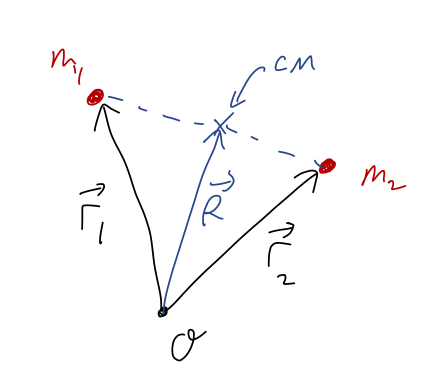
Using our formulas above, we have
\[ \begin{aligned} \vec{R} = \frac{m_1}{m_1 + m_2} \vec{r}_1 + \frac{m_2}{m_1 + m_2} \vec{r}_2 \end{aligned} \]
Notice that if we take \( m_1 \rightarrow 0 \), then the CM position approaches \(\vec{R} = \vec{r}_2\), and vice-versa. So the CM position tends to be closest to the heavier mass. On the other hand, if \(m_1 = m_2\), then
\[ \begin{aligned} \vec{R} = \frac{1}{2}(\vec{r}_1 + \vec{r}_2) \end{aligned} \]
which is exactly in the center between the masses.
We can make a couple more nice observations in the two-mass case by changing coordinates. First, let's try setting \( \vec{r}_1 = 0 \), i.e. putting mass 1 at the origin of our coordinates. Then we have
\[ \begin{aligned} \vec{R} \rightarrow \frac{m_2}{m_1 + m_2} \vec{r}_2 \end{aligned} \]
so \( \vec{R} \) points in the same direction as \( \vec{r}_2 \). In other words, the position of the center of mass is along the line between \( m_1 \) and \( m_2 \).
Finally, let's put our coordinate origin at the geometric center, exactly halfway in between \( \vec{r}_1 \) and \( \vec{r}_2 \) as shown:
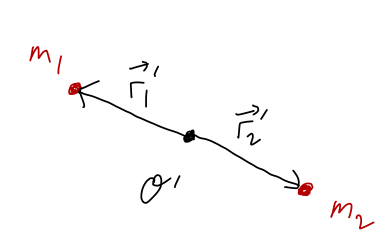
Measured from this point, we have \( \vec{r}'_2 = -\vec{r}'_1 \). Using this relation in the general formula gives
\[ \begin{aligned} \vec{R} = \frac{m_1}{m_1 + m_2} \vec{r}'_1 - \frac{m_2}{m_1 + m_2} \vec{r}'_1 \end{aligned} \]
In general, the CM is not at the geometric center; it will be closer to the heavier mass out of \( m_1 \) or \( m_2 \). However, in the special case where \( m_1 = m_2 \), the two terms are equal and opposite and cancel completely. The situation where this cancellation happens is said to exhibit reflection symmetry or mirror symmetry about the origin; mirror reflection takes \( \vec{r} \rightarrow -\vec{r} \), so with \( \vec{r}'_2 = -\vec{r}'_1 \) we can think of mass 2 as a 'reflection' of mass 1 if they are identical.
This probably seems like a really special case, but notice what happens if we add two more masses along a different line:
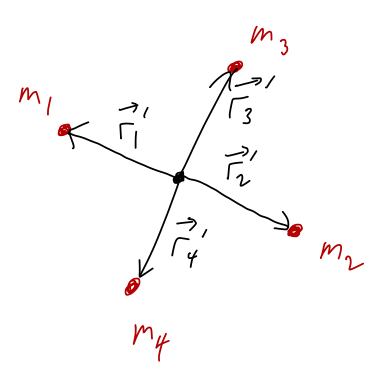
With \( \vec{r}'_4 = -\vec{r}'_3 \), we have
\[ \begin{aligned} \vec{R} = \frac{m_1 - m_2}{M} \vec{r}'_1 + \frac{m_3 - m_4}{M} \vec{r}'_3 \end{aligned} \]
and once again, if the pairs \((m_1, m_2)\) and \((m_3, m_4)\) are reflection symmetric, then both pairs contribute zero to the CM position and we find \( \vec{R} = 0 \).
What we're seeing is a very general and powerful rule that applies to calculating the center of mass: if we have two equal masses \(m_1 = m_2\) at exactly opposite positions, \(\vec{r}_1 = -\vec{r}_2\), then their total contribution to the CM is zero.
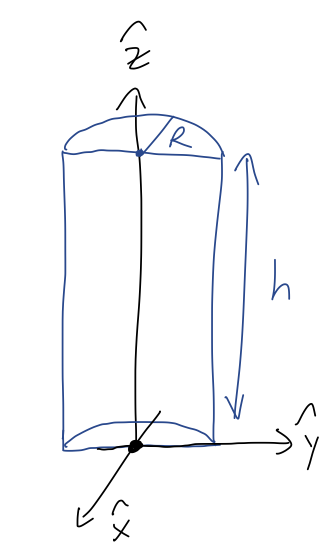
Now let's move on to the continuous case. I'll start with a simple example which will be easy to make more complicated, which is a cylinder of uniform density:
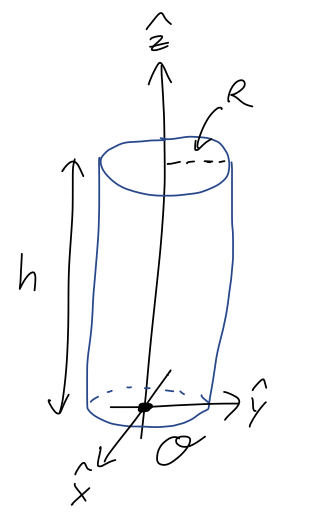
Let's just set up and do the integrals, and then we'll think about the results. With uniform (i.e. constant) density, we have simply \( \rho(\vec{r}) = \rho \). We put the origin at the center of the bottom of the cylinder, as shown. Starting with the x-position:
\[ \begin{aligned} X_{CM} = \frac{1}{M} \int x\ dm = \int x (\rho\ dV) = \frac{\rho}{M} \int_0^{2\pi} d\phi \int_0^R dr \int_0^h dz\ r x \end{aligned} \]
using cylindrical coordinates to expand out \( dV \), which gives us a factor of \( r \). (I am also using \( r \) instead of \( \rho \) for the cylindrical radius, because we have another \( \rho \) already, the density!) Thinking back to the definition of cylindrical coordinates, we recall that \( x = r \cos \phi \), so the integrand is \( r^2 \cos \phi \). All of the integrals are separate and easy to do:
\[ \begin{aligned} X_{CM} = \frac{\rho}{M} h \left. \left( \frac{1}{3} r^3 \right) \right|_0^R \left.\left( \sin \phi \right)\right|_0^{2\pi} \end{aligned} \]
But the last term is \( \sin 2\pi - \sin 0 = 0 \), so we just have \( X_{CM} = 0 \). I'll leave it as a short exercise to convince yourself that similarly, \( Y_{CM} \) ends up proportional to \( \cos 2\pi - \cos 0 \), so that also \( Y_{CM} = 0 \). Finally, for the \( z \) position, we have
\[ \begin{aligned} Z_{CM} = \frac{\rho}{M} \int_0^{2\pi} d\phi \int_0^R dr \int_0^h dz\ r z \\ = \frac{2\pi \rho}{M} \left(\frac{1}{2} h^2\right) \left( \frac{1}{2} R^2 \right) = \frac{\pi \rho h^2 R^2}{2M}. \end{aligned} \]
To simplify further, we recognize that \( \rho \) and \( M \) are related to each other. For constant density we just have \( M = \rho V \), but I'll just do the integral:
\[ \begin{aligned} M = \int \rho dm = \int_0^{2\pi} d\phi \int_0^R dr \int_0^h dz\ \rho r = \pi R^2 h \rho. \end{aligned} \]
Plugging back in then gives us the much simpler result
\[ \begin{aligned} Z_{CM} = \frac{h}{2}. \end{aligned} \]
Zero is a pretty special result, so let's go back and think about why we found that for \( X_{CM} \) and \( Y_{CM} \). Before we convert to cylindrical coordinates, the integral for \( X_{CM} \) can be written in the form:
\[ \begin{aligned} X_{CM} = \frac{\rho}{M} \int_{-R}^R dx\ x \int dy \int dz = \frac{\rho}{M} \int_{-R}^R dx\ x f(x) \end{aligned} \]
where \( f(x) \) is the result of doing the \( y \) and \( z \) integrals out first. We get a function of \( x \) because the \( y \) limits of integration depend on \( x \). (The function \( f(x) \) isn't too difficult to find explicitly, and if you need practice with integrating go ahead and try it!) All we need to know is that \( f(x) \) is reflection symmetric,
\[ \begin{aligned} f(-x) = f(x). \end{aligned} \]
This has to be true because if we reflect the cylinder along the \( x \)-axis about the origin, it looks completely identical. (I say "reflect along the \( x \)-axis", but really what this means is you should imagine a plane perpendicular to the x-axis and containing the origin. That plane is acting like a mirror for the reflection.)
Knowing this one geometric fact, we have
\[ \begin{aligned} X_{CM} \propto \int_{-R}^R dx\ x f(x) = \int_{-R}^0 dx\ x f(x) + \int_0^R dx\ x f(x) \\ = \int_R^0 (-dx) (-x) f(-x) + \int_0^R dx\ x f(x) \\ = -\int_0^R dx\ x f(x) + \int_0^R dx\ x f(x) = 0. \end{aligned} \]
(the symbol \( \propto \) means "is proportional to", i.e. ignoring the \( \rho/M \) out front.) Similarly, the fact that the cylinder is identical if we reflect along the \( \hat{y} \)-axis lets us predict immediately that \( Y_{CM} = 0 \), even before we actually do the integral. This doesn't work for the \( \hat{z} \) direction, because if we reflect about the origin, (i.e. through a plane containing the origin and perpendicular to \( \hat{z} \)), our sketch looks different:
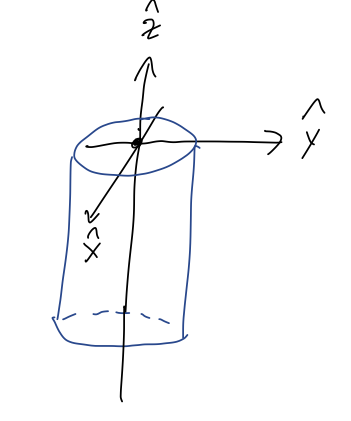
On the other hand, if we put the origin halfway up the cylinder's axis at \( z=h/2 \), then we have the reflection symmetry and would find \( Z_{CM} = 0 \) - exactly in agreement with our third result above. In math terms, this is the difference between integrating from \( 0 \) to \( h \) and from \( -h/2 \) to \( h/2 \) - we need the symmetric interval of integration for the two halves of the integral to cancel off.
There's a more physical explanation for why the mathematics works out this way; it's exactly the same cancellation that we saw before in our point-mass examples. Because of the reflection symmetry in the \( \hat{x} \) direction, for any little bit of mass \( dm \) that we identify in the cylinder, there is a corresponding (and identical) bit of mass \( dm \) on the other side of the origin. As we saw above, the contribution of these two masses to the CM location will balance and cancel off.
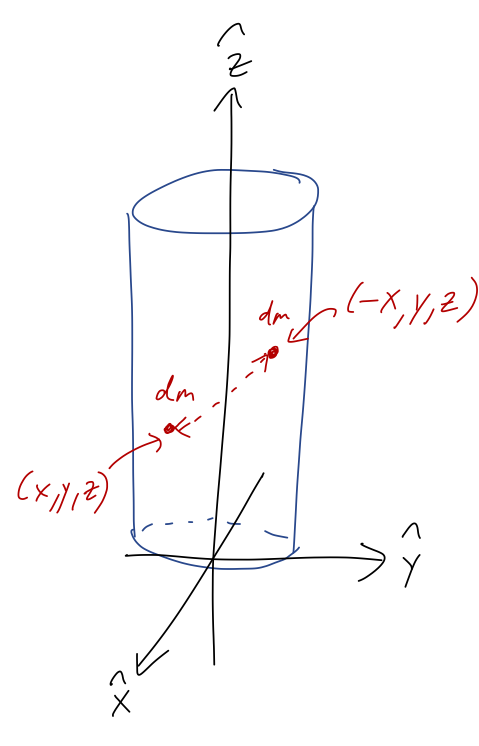
Likewise, we see that reflecting about the CM at \( Z_{CM} = h/2 \), the mass on either side in the \( \hat{z} \) direction is perfectly balanced. We could have used this observation to see that \( Z_{CM} = h/2 \), again without having to actually do any integrals. Symmetry is powerful!
Exercise: find the CM
Now suppose we have a half-cylinder, cut in half through the circular direction as shown:
What are \( Y_{CM} \) and \( Z_{CM} \)? (If you finish quickly, you can try to find \( X_{CM} \) too; I'll do that as an example next.)
For the two directions given, we can use symmetry to find the answer without doing any math! In the \( \hat{y} \) direction, we notice that we have reflection symmetry about the axis through the middle of the half-cylinder: every point \( (x,y,z) \) in the cylinder has a matching point at \( (x,-y,z) \). So \( Y_{CM} = 0 \) by symmetry.
Similarly, in the \( \hat{z} \) direction we still have reflection symmetry about the plane halfway through the half-cylinder, so \( Z_{CM} = h/2 \) as in the previous case.
We can't apply these arguments to \( X_{CM} \), because there's nowhere that we can put a mirror perpendicular to \( \hat{x} \) that will reflect our object without giving a different image! So symmetry helped us twice, but we have to do one integral. Let's set it up: we have
\[ \begin{aligned} X_{CM} = \frac{1}{M} \int \rho\ x\ dV \\ = \frac{\rho}{M} \int_{\pi/2}^{3\pi/2} d\phi \int_0^R r dr \int_0^h dz (r \cos \phi) \end{aligned} \]
where the only adjustment we need to make for the half-cylinder is that our polar angle runs from \( \pi/2 \) to \( 3\pi/2 \) (look carefully at the diagram!) Doing the integrals gives
\[ \begin{aligned} X_{CM} = \frac{\rho}{M} \left.\frac{hR^3}{3} (\sin \phi) \right|_{\pi/2}^{3\pi/2} \\ = \frac{2hR^3\rho}{3M} \end{aligned} \]
Since this is a half-cylinder, its volume is just half of the standard volume, which means
\[ \begin{aligned} M = \frac{1}{2} \pi R^2 h \rho \end{aligned} \]
allowing us to simplify the answer to
\[ \begin{aligned} X_{CM} = \frac{4R}{3\pi}. \end{aligned} \]
which is about 0.4 times \( R \) - not quite halfway up the semicircle, which makes sense since there's more mass around \( x=0 \) than \( x=R \).