Continuing from last time, we defined the gravitational potential (not the potential energy!) which is related to the gravitational field as \( \vec{g} = -\vec{\nabla} \Phi \). For a source mass \( M \) at the origin, the potential takes the form
\[ \begin{aligned} \Phi(r) = -\frac{GM}{r} \end{aligned} \]
so that \( U(r) = m\Phi(r) \). Now if we have an extended object, as we saw before:

then the potential at position \( \vec{r} \) due to the infinitesmal source \( dm \) is
\[ \begin{aligned} d\Phi(\vec{r}) = -\frac{G dm}{s} = -\frac{G dm}{|\vec{r} - \vec{r}'|}, \end{aligned} \]
and thus the total potential is
\[ \begin{aligned} \Phi(\vec{r}) = -G \int \frac{dV' \rho(\vec{r}')}{|\vec{r} - \vec{r}'|}. \end{aligned} \]
This is much nicer to evaluate than the integrals we had to do for \( \vec{g} \)! Now we have no vector components to worry about - just a single scalar quantity. We can then take the gradient of our result (with respect to \( \vec{r} \)) to find the gravitational field \( \vec{g} \).
Let's do an example to see how this approach works in practice.
Example: gravitational potential of a sphere
Let's find the \( \vec{g} \) field due to a sphere of constant mass density \( \rho \), using the gravitational potential \( \Phi \). Once again, let's assume we're working along the \( z \)-axis, so \( \vec{r} = z\hat{z} \).
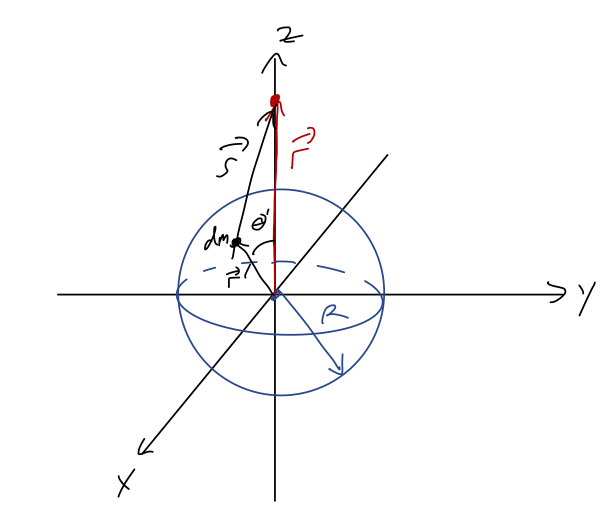
We start by setting up the integral, using the sketch as a guide:
\[ \begin{aligned} \Phi(\vec{r}) = -G \int \frac{dV' \rho}{|\vec{r} - \vec{r}'|}. \end{aligned} \]
Let's work in spherical coordinates since we have a sphere. We can re-express the denominator as
\[ \begin{aligned} |\vec{r} - \vec{r}'|^2 = (r' \sin \theta' \cos \phi')^2 + (r' \sin \theta' \sin \phi')^2 + (z - r' \cos \theta')^2 \\ = r'^2 + z^2 - 2zr'\cos \theta' \end{aligned} \]
(you may remember this as an example of the law of cosines), so then
\[ \begin{aligned} \Phi(z) = -G\rho \int_0^{2\pi} d\phi \int_0^R dr' \int_0^{\pi} d\theta' \frac{r'^2 \sin \theta'}{\sqrt{r'^2 + z^2 - 2zr' \cos \theta'}} \end{aligned} \]
This integral is surprisingly tricky, and is one of the first examples we've encountered where you'll run into a horrible mess if you try to brute force it in Mathematica! There's a very, very useful change of variables that we can make here. Let's define the distance \( s \) as before to be
\[ \begin{aligned} s^2 = |\vec{r} - \vec{r}'|^2 = r'^2 + z^2 - 2zr' \cos \theta'. \end{aligned} \]
Let's suppose that we're holding \( r' \) fixed and just treating \( \theta' \) as a variable. (As long as we do the \( \theta' \) integral first, this is perfectly valid!) Then differentiating both sides gives the much simpler result
\[ \begin{aligned} 2s ds = 2zr' \sin \theta' d\theta' \\ \Rightarrow r' \sin \theta' d\theta' = \frac{s}{z} ds \end{aligned} \]
which lets us rewrite the integral as, doing the \( \phi \) integral since nothing else depends on it,
\[ \begin{aligned} \Phi(z) = -2\pi G \rho \int_0^R dr' \int_{s_{\rm min}}^{s_{\rm max}} r' ds (s/z) \frac{1}{s} \\ = -\frac{2\pi G \rho}{z} \int_0^R dr' r' (s_{\rm max} - s_{\rm min}). \end{aligned} \]
To continue, we need to find the limits of integration. They started out as \( \theta' = 0,\pi \), so we can just plug in and solve:
\[ \begin{aligned} s_{\rm min}^2 = r'^2 + z^2 - 2zr' = (r' - z)^2 \\ s_{\rm max}^2 = (r' + z)^2 \end{aligned} \]
Now, \( s_{\rm min} \) and \( s_{\rm max} \) are both distances, so they have to be positive. So \( s_{\rm max} = r' + z \), always. However, for the other limit, the answer depends on what \( z \) is. If \( z > r' \), then we have \( s_{\rm min} = z-r' \), otherwise it's equal to \( r'-z \).
Let's assume that \( z > R \), i.e. we're looking for the potential outside the sphere. Then we have
\[ \begin{aligned} \Phi(z) = -\frac{2\pi G \rho}{z} \int_0^R dr' r' [(r'+z) - (z-r')] \\ = -\frac{2\pi G \rho}{z} \int_0^R dr' 2r'^2 \\ = -\frac{4\pi G \rho}{3z} R^3. \end{aligned} \]
Some of these numerical factors should look familiar: the combination \( 4\pi R^3/3 \) is just the volume \( V \) of the sphere, and since \( V \rho = M \), we have finally
\[ \begin{aligned} \Phi(z) = -\frac{GM}{z}. \end{aligned} \]
Before we move on, an important observation to make is that there is nothing special about the \( z \) direction for a sphere. If I chose a point in any arbitrary direction above the surface of the sphere to find the potential at, I could have just called that direction \( z \) and I would get the same answer.
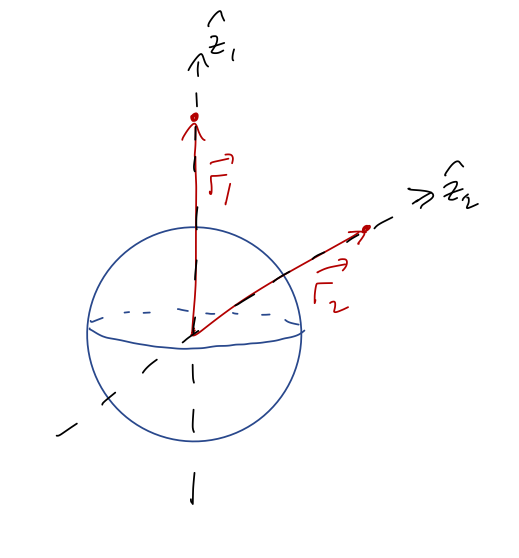
Thanks to this rotational symmetry, the \( z \)-axis answer is the answer everywhere: for any point a distance \( r>R \) from the center of the sphere, we have
\[ \begin{aligned} \Phi(r) = -\frac{GM}{r}. \end{aligned} \]
This is the same potential as if all of the mass were concentrated at the center of the sphere - even if we're really close to the surface!
Since this is something of a surprising result, let's step back from the math and try to understand the physics here. First of all, we replaced the spherical angle \( \theta \) with the distance \( s \). This is the same general definition of \( s \) we've used before: the distance from infinitesmal mass \( dm \) to the point at which we're calculating the potential or force. However, we should first notice that we're working in three dimensions but our sketch only has two. The third dimension amounts to rotating in the \( \phi' \) direction, which doesn't change the diagram thanks to the symmetry of the sphere. This means that \( s \) is really pointing to an infinitesmal ring, not a point:

Next we remember that \( s \) replaced the other angle, \( \theta' \), and that we think of \( s \) as defined given a constant value of \( r' \), the radius from the center. Taken together, the integral over \( ds \) describes an infintesmal spherical shell at fixed radius \( r' \). In other words, we can rewrite our integral formula for \( \Phi(r) \) as
\[ \begin{aligned} \Phi(r) = \int_0^R dr' \int_{s_{\rm min}}^{s_{\rm max}} \frac{-2\pi G \rho r' ds}{r} \\ = \int_0^R dr' \frac{-4\pi G \rho r'^2}{r} \\ = \int_{r'=0}^{r'=R} d\Phi_s(r',r) \end{aligned} \]
where \( d\Phi_s(r',r) \) is the potential at distance \( r \) from the origin due to an infinitesmally thin spherical shell of radius \( r' \). This makes sense, because we've already seen that if we have multiple sources of gravity (or any conservative force), the total potential energy \( U \) is just the sum of the individual potential energies due to each source. So another way to think of calculating the sphere's potential is to first find the potential due to a thin shell, and then just sum up all the shells from 0 to \( R \).
Since the thin-shell potential is important, I'll point out that it's also simpler than it looks. The mass of a thin spherical shell that goes from \( r' \) to \( r'+dr' \) is
\[ \begin{aligned} dM = \frac{4}{3} \rho \pi [(r'+dr')^3 - r'^3] \approx 4 \pi \rho r'^2 dr' \end{aligned} \]
so we can write
\[ \begin{aligned} d\Phi_s(r',r) = -\frac{G}{r} dM \end{aligned} \]
again just like the point-mass potential. (Note: this is a special case)
The thin-shell picture makes it easy for us to work out variations on this simple problem, but we only have half of the picture so far:
Example: hollow sphere
What is the gravitational potential \( \Phi(R,r) \) inside a thin spherical shell of radius \( R \) and constant density \( \rho \)?
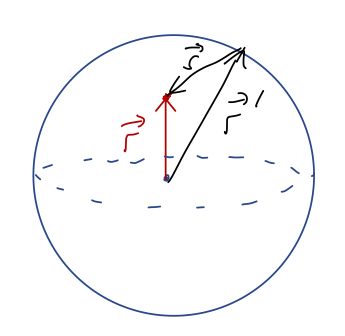
We need to be careful here and go back to the integral over \( s \) that we found:
\[ \begin{aligned} \Phi(r) = \int_0^R dr' \int_{s_{\rm min}}^{s_{\rm max}} -\frac{2\pi G \rho(r') r' ds}{r} \end{aligned} \]
Now, since this is a very thin shell, the density \( \rho(r') \) is zero everywhere except very close to \( r'=R \). So we can actually just take \( r' \) to be equal to the constant \( R \), and get rid of the \( r' \) integral:
\[ \begin{aligned} \Phi(r) = \int_{s_{\rm min}}^{s_{\rm max}} \frac{-2\pi G \rho R ds}{r} \end{aligned} \]
Now, remember that \( s_{\rm max} \) and \( s_{\rm min} \) have to be positive! From our previous work or just from the diagram, we know that \( s_{\rm max} = r' + r \). However, unlike the previous calculation we now have \( s_{\rm min} = r' - r \), with the opposite sign since \( r \) is always smaller. So when we substitute back in and use \( r'=R \), we find
\[ \begin{aligned} \Phi(r) = -\frac{2\pi G \rho R}{r} [(R + r) - (R - r)] \\ = -4\pi G \rho R. \end{aligned} \]
Importantly, this only depends on the size of the shell and other constants - the position \( r \) doesn't appear at all! So the potential inside of a spherical shell is constant,
\[ \begin{aligned} \Phi(r) = -\frac{GM}{R}. \end{aligned} \]
This applies to a hollow sphere with finite width as well, since we can write that potential as an integral over a bunch of spherical shells, all of which will contribute constants that don't depend on the position \( r \) inside the sphere. So inside of a sphere, there is no gravitational force at all!
These suprisingly simple results are actually consequences of some powerful math at work, which we'll explore next.
Gauss's law and gravity
We've emphasized that the potential tends to be easier to work with than trying to calculate \( \vec{g} \) directly. However, one good reason to use \( \vec{g} \) in certain cases is to invoke some very powerful results from vector calculus. We already mentioned Stokes' theorem briefly in our discussion of curl and conservative forces. Now I'll borrow another result, again without proof, known as Gauss's law:
\[ \begin{aligned} \oint_{\partial V} \vec{g} \cdot d\vec{A} = -4\pi G \int_V \rho(\vec{r}) dV = -4\pi G M_{\rm enc}. \end{aligned} \]
Let's unpack the dense notation here, a lot of which looks very similar to Stokes's theorem. Here \( V \) denotes some volume in three-dimensional space, and \( \partial V \) is the boundary of this volume, which must be a closed surface (in the same way that the boundary \( \partial A \) of a surface is a closed loop); the ring on the integral reminds us of this. We know what everything else is, except for \( M_{\rm enc} \): this is the "enclosed mass", i.e. the total of all the mass contained in the region \( V \).
Where does this result come from? To understand that, we need to introduce our last vector derivative, the divergence, which we get as the dot product of the gradient with another vector. In Cartesian coordinates, we would have
\[ \begin{aligned} \vec{\nabla} \cdot \vec{g} = \frac{\partial g_x}{\partial x} + \frac{\partial g_y}{\partial y} + \frac{\partial g_z}{\partial z} \end{aligned} \]
Gauss's law is actually a special case of a more general vector calculus result known as the divergence theorem, stated without proof: for any vector field \( \vec{b}(\vec{r}) \), the divergence theorem states that
\[ \begin{aligned} \oint_{\partial V} \vec{b}(\vec{r}) \cdot d\vec{A} = \int_V (\vec{\nabla} \cdot \vec{b}(\vec{r})) dV \end{aligned} \]
This matches on to Gauss's law if we make the identification
\[ \begin{aligned} \vec{\nabla} \cdot \vec{g} = -4\pi G \rho(\vec{r}). \end{aligned} \]
This equation is sometimes also called Gauss's law, because one version implies the other one thanks to the divergence theorem. This last equation is also interesting, because we can view it as a differential equation that can be solved for \( \vec{g} \) given \( \rho(\vec{r}) \) - yet another way to obtain the gravitational vector field!
Next time, we'll continue to see how Gauss's law can be used in practice.