Last time, we finished talking about gravity near the Earth's surface as an example of an effective theory, ending on the expansion:
\[ \begin{aligned} g(z) \approx g \left( 1 - \frac{2z}{R_E} + ... \right) + C_1 \frac{z}{R_{ES}} + C_2 \frac{\ell_P}{z} + ... \end{aligned} \]
We argued that effects from very separated scales like \( R_{ES} \) are small, because the ratio \( z/R_{ES} \) is very small for \( z \) near the Earth's surface. This isn't a guarantee that there's no possible effect from the other physical scales present, of course. In this example, if \( R_{ES} \) was significantly smaller, there might be terms like \( R_{ES} / R_E \) which aren't necessarily completely negligible. But this doesn't depend on \( z \) - \( z \) is a scale that we define as part of the effective theory. So such a correction could change the leading-order constant term \( g \), or the coefficients of other terms, but it can't alter the form of the \( z \)-dependence, as long as we still have scale separation between \( z \) and \( R_{ES} \).
This leads to a second way to think about effective theory. Even if we didn't know the full Newtonian theory of gravity, experimenting with gravity at different heights above the Earth's surface would still tell us that there is some dependence on the height. We could have instead built a top-down effective theory, where we don't know the fundamental theory at all, but we use experiment and symmetry to formulate a theory. From experiments on the Earth, it's easy to discern that (1) \( g \) is almost a constant downwards acceleration, and (2) there is some dependence on the height \( z \). Based on those two observations, we can write a very general Taylor series in \( z \) over an unknown length scale \( L \):
\[ \begin{aligned} g(z) = g + g_1 \frac{z}{L} + g_2 \frac{z^2}{L^2} + ... \end{aligned} \]
Now we go out and do experiments to measure the acceleration due to gravity at lots of different heights, and then we find the values \( g_0, g_1, g_2 \) that describe our data. Once we've done that exercise, we now have a working theory of gravity that we can use to make predictions - without knowing anything about the more fundamental theory!
Of course, this will break down at some point; when \( z \) approaches the unknown length scale \( L \), the expansion won't converge and our predictions will fail. But this is actually a feature of top-down effective theories: they let you know when they begin to break! And by doing enough experiments to infer the \( z \)-values where this theory begins to fail, we can actually discover what the value of \( L \) is, which can be a big hint as to what the more fundamental theory is. (In this case, we know the right answer already: \( L \) is \( R_E \), the Earth's radius.)
There is another way that our effective theory can fail: if we neglect to include some physical effect which is actually important. In this case, we have done just that: the Earth is not perfectly spherical, and its density is also not uniform. So if we just keep our height above sea level \( z \) fixed and try to measure \( g(z) \), we will find different results depending on where we are on the Earth! After doing some experiments, we would need to revise our effective theory to \( g(x,y,z) \), accounting for the additional variation with our position on the Earth's surface.
Effective theory is a seemingly simple idea: basically an application of series expansion once again. But again, this is a really important idea in physics! Whenever we write down Newton's laws, we're also ignoring long-distance effects from things like the Sun's gravitational field, and we're ignoring quantum effects that will show up around atomic distance scales. So all of Newtonian physics is in fact an effective theory!
In fact, all of the "fundamental" forces are effective theories too, as far as we know. A famous example is gravity itself; if we try to calculate using the theory of gravity on scales where quantum mechanics is also important, then we find that the resulting effective theory diverges badly if we even ask theoretical questions about distances close to \( \ell_P \), the Planck length I mentioned above. This is such an enormously short distance scale that we have no experiments that can possibly probe it, so far - but effective theory gives us a tantalizing hint that gravity has to change somehow if we can start to look at those really short distances.
Dark matter
The story of dark matter begins with a really simple physics question: how do we know the mass of the Sun \( M_{\odot} \)? I mentioned before that for the Earth, there's only one reliable measurement of its mass, which is using the force of gravity exerted by the Earth. We can do the same for the Sun, by looking at the Earth's orbit: the force on the Sun due to the Earth is
\[ \begin{aligned} \vec{F}_g = -\frac{GM_{\odot} M_E}{R_{ES}^2} \end{aligned} \]
Now, the orbit of the Earth isn't perfectly circular, but it's pretty close; if we assume that it is circular, then this is also a centripetal force:
\[ \begin{aligned} \vec{F}_g = \vec{F}_c \Rightarrow \frac{GM_{\odot} M_E}{R_{ES}^2} = \frac{M_E v_E^2}{R_{ES}} \end{aligned} \]
or solving for the mass of the Sun,
\[ \begin{aligned} M_{\odot} = \frac{v_E^2 R_{ES}}{G}. \end{aligned} \]
Finding the speed of the Earth's orbit is easy: we know it completes a full orbit in 1 year, or 365.25 days. A full orbit is a change in angle of \( 2\pi \), so the Earth's angular speed is
\[ \begin{aligned} \omega_E = \frac{2\pi}{365.25\ {\rm days}} \approx 2.0 \times 10^{-7} / s. \end{aligned} \]
Since \( v_E = \omegaE R{ES} \), we now know \( vE \) in terms of \( R{ES} \). Determining the latter is actually tricky, although there are estimates dating back as much as 2300 years ago; I won't go into details, but it involves geometric arguments with the Sun, Earth, and another astronomical body making a triangle. The advent of radar ranging to other planets can be combined with modern versions of these geometric calculations to yield a fairly accurate result, which I already quoted above: \( R_{ES} \approx 1.48 \times 10^{11} \) m.
Putting things together, we find
\[ \begin{aligned} M_{\odot} = \frac{\omega_E^2 R_{ES}^3}{G} = 1.9 \times 10^{30}\ {\rm kg}. \end{aligned} \]
For the Sun, we actually have a second way to estimate its mass: based on its size and density. Again using geometry, the radius of the Sun itself can be determined to be \( R_{\odot} = 7.0 \times 10^5 \) km. Thus, the mass will be related to the density as
\[ \begin{aligned} M_{\odot} = \rho_{\odot} V_{\odot} = \frac{4}{3} \pi R_{\odot}^3 \rho_{\odot}. \end{aligned} \]
We can estimate the density of the Sun because we know what it's made of: primarily hydrogen and helium, heated into a superhot plasma. Now, this is definitely not a simple exercise: the temperature will have significant effects on the density, and so will the additional pressure generated by the huge gravitational pull of the Sun. But we have fairly complete models of the Sun's interior, and it's certainly possible to do the calculation carefully and get an estimate - see here for a taste of how such models work - of about 1400 kg/\( {\rm m}^3 \). This once again gives a result of \( M_{\odot} \sim 2 \times 10^{30} \) kg.
This is a nice consistency check between our model of gravity and our model of the Sun. It also suggests a similar approach to a much more ambitious question: how much mass is in a galaxy like the Milky Way? The second method for weighing a galaxy is straightforward: you estimate how many stars there are, multiply by the mass of an average star (very roughly the mass of the Sun, but there are detailed models of stellar populations that can improve this!), and that gives you one version of \( M_{\rm galaxy} \).
The gravitational way of estimating a galaxy's mass turns out to be a bit more involved. But we have a lot of extra information: since we can infer the motion of all of the visible stars in a galaxy, we can see "inside" the galaxy to probe its complete gravity field instead of having to rely only on objects well outside the galaxy, as we did for the Earth-Sun case.
Let's restrict our attention to a certain fairly common kind of galaxy known as an elliptical galaxy, which can be nearly spherical - in fact, let's assume it is spherical for the sake of our calculation. (I'll comment on this assumption later.)
To find the gravitational field, we need to consider another variant of the sphere problem: finding the field inside of a solid sphere. We can set this up simply using Gauss's law. Let's take a sphere of radius \( R \) and consider \( r < R \) as shown:
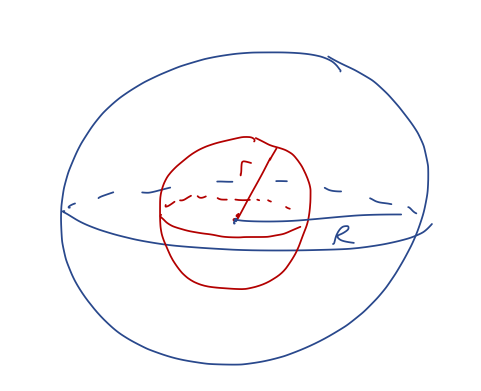
Applying Gauss's law using the spherical surface at distance \( a \), we have \( d\vec{A} = r^2 \sin \theta \hat{r} \) and \( \vec{g} = g(r) \hat{r} \), so
\[ \begin{aligned} \oint_{\partial V} \vec{g} \cdot d\vec{A} = -4\pi G \int_V \rho(\vec{r}) dV \\ 4\pi r^2 g(r) = -4\pi G \int_0^{2\pi} d\phi' \int_0^\pi d\theta' \int_0^r dr'\ \rho(\vec{r}'') r'^2 \sin \theta' \end{aligned} \]
If \( \rho \) is constant, then we can pull it out of the integral which will just become the volume of the inner sphere:
\[ \begin{aligned} 4\pi r^2 g(r) = -4\pi G \rho \left( \frac{4}{3} \pi r^3 \right) \end{aligned} \]
or rearranging,
\[ \begin{aligned} g(r) = -\frac{4}{3} \pi G \rho r. \end{aligned} \]
So the strength of the gravitational field actually increases with distance! We can't observe the gravity field directly, just the motion of the stars, so we have one more step, to relate this to the speed. The main dynamics of a galaxy is not that different from our solar system: the stars follow orbits around the galactic center of mass. If we make the assumption of an approximately circular orbit, then the force of gravity must be equal to the centripetal force,
\[ \begin{aligned} |\vec{F}_g| = |\vec{F}_c| \\ m|\vec{g}(r)| = \frac{mv^2}{r} \\ \frac{4}{3} \pi G \rho r = \frac{v^2}{r} \\ v = \sqrt{\frac{4\pi G \rho}{3}} r. \end{aligned} \]
We can measure \( v \) and \( a \), and then extract the density \( \rho \) from this equation to find the galaxy mass. Of course, this is only true inside the sphere, or equivalently in the middle of the galaxy where the density really is more or less constant. But if we look at stars close to the edge of the galaxy, we can treat them as being just outside a sphere, and we have our previous result
\[ \begin{aligned} g(a) = -\frac{GM_{\rm enc}}{r^2} \end{aligned} \]
for \( r > R \). Relating to the speed in the same way as before, we have
\[ \begin{aligned} \frac{GM_{\rm enc}}{r^2} = \frac{v^2}{r} \\ v = \sqrt{\frac{GM_{\rm enc}}{r}}. \end{aligned} \]
So if we can get good observations of stars at the edge of a galaxy, we can just measure their speeds directly to determine the mass. Overall, if we look at all of the stars, if the density is constant out to the edge of the visible galaxy at \( R \), we expect the profile of speed vs. distance to look like this:
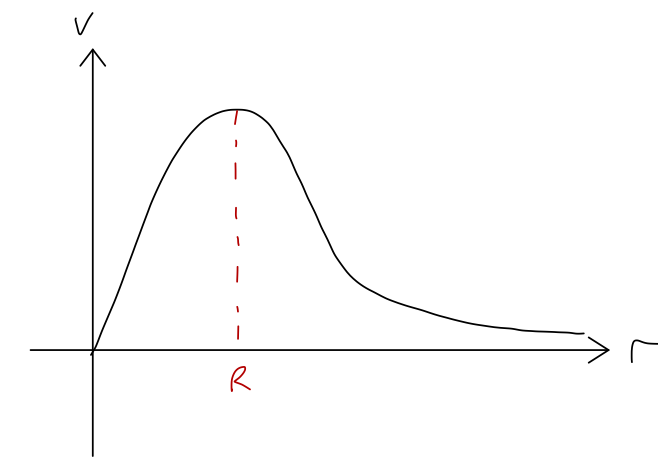
(Our prediction isn't this smooth near \( R \), but a smooth function is more realistic, due to measurement error and the fact that the density of a galaxy isn't really uniform.) So far, so good. But what do we see if we actually do this experiment? Here is a plot of \( v \) vs. \( r \) for the galaxy NGC 3198: this is a spiral galaxy and not an elliptical, so I'm cheating a little; spirals seem to be easier to make this sort of observation of the full rotation curve in, probably because we get an unobstructed view of stars all the way to the center.
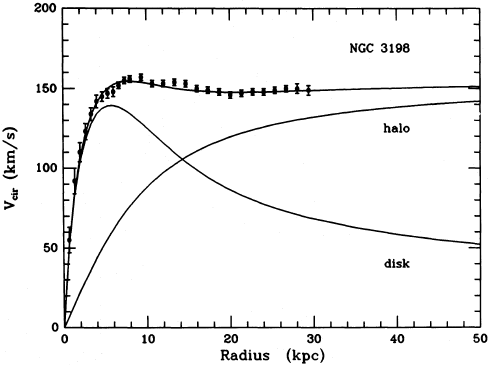
(from https://jila.colorado.edu/~ajsh/astr1200_18/dm.html, and originally https://ui.adsabs.harvard.edu/abs/1985ApJ...295..305V/abstract.)
The "disk" line shows the expected dependence; the data points show the observed results. You can see from the disk line that in this model, \( R \) for the galaxy is about 6 kpc (kilo-parsecs, a parsec is short for "parallax arcsecond" and is one of those somewhat arcane astronomy units; a parsec is about 3.3 light-years.) For small \( r \) the data agree well with the disk model, with speed increasing with distance, but then instead of the expected turnover, the velocity just becomes constant out to well beyond where the visible edge of the dense part of the galaxy is found!
One possibility is that we've neglected something: there is another force that we don't know about, or our model of gravity is just wrong. This is still a possibility, although the preponderance of evidence is strongly in favor of the second option: dark matter. That is to say, what we have wrong isn't the force law, but the density function: there must be some additional source of gravity that extends out beyond where the visible stars end. Quite far beyond, in fact; for most galaxies, a full explanation requires an enormous dark matter "halo" surrounding the visible galaxy:
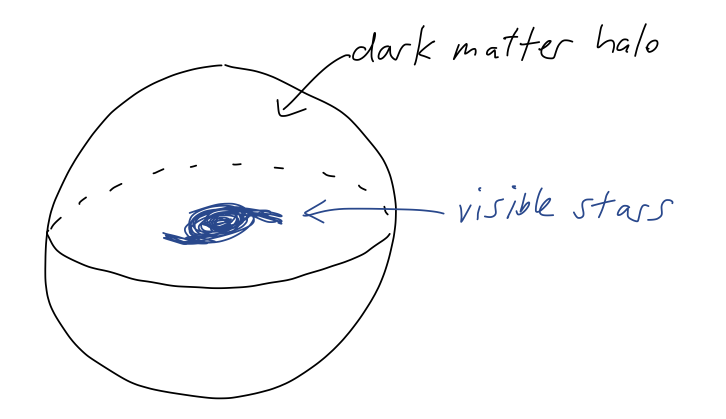
This has to be "dark" because it doesn't emit or absorb light at all, or at best it does so very weakly; astronomical observations across the spectrum of light show nothing at all where the gravitational mass should be plentiful. This also brings me back to the comment about spherical galaxies: even for a spiral galaxy, the dark matter halo itself is still spherical (and much larger than the galaxy itself!), so our calculation still applies.
We can even guess what the density of the missing dark matter is using what we've derived so far: as you can see from the plot, the contribution to the speed from the halo goes roughly as \( \sqrt{r} \). Working backwards, this requires a constant gravitational field, which in turn means that for the dark matter halo,
\[ \begin{aligned} \rho(r) \propto \frac{1}{r}. \end{aligned} \]
Of course, this is only one galaxy; there are other examples where \( v(r) \) becomes constant (which would require \( \rho(r) \propto 1/r^2 \)) or begins to drop at very large distances. A commonly adopted model which works well for a large number of galaxies is the Navarro-Frenk-White profile, or NFW profile for short:
\[ \begin{aligned} \rho_{\rm NFW}(r) = \frac{\rho_0}{(r/a)(1 + r^2/a^2)} \end{aligned} \]
introducing a second length scale \( a \), the "scale radius". This model can be argued as a simple but general parametrization of the behavior of so-called "cold and collisionless" dark matter - which can be tested using numerical simulations consisting of N masses only interacting through gravity.
Since it's an active topic of research, I should say a little more about what we do know about dark matter. So far, the answer is "not very much"; experimental searches that attempt to capture the passing of a dark matter particle through an Earth-based detector have so far yielded nothing, except strong confirmation that it is indeed "dark" - any other interaction it has with ordinary matter must be very weak indeed.
However, we have a large amount of evidence for the gravitational effects of dark matter. In addition to observations of galactic structure (for which there are many examples):
- There is evidence for an imprint of dark matter on the cosmic microwave background, a uniform background noise that was formed in the very early universe.
- Over the very largest distance scales, the galaxies that make up our universe are not spread around randomly; instead, they seem to be organized into large, invisible filaments. This filamentary structure is consistent with simulations of the formation of the universe that include dark matter.
- Finally, according to the theory of general relativity (which replaces Newtonian gravity like special relativity replaces Newtonian mechanics), the path of a ray of light bends in a gravity field, an effect known as "gravitational lensing". This is a complicated subject, but there are a number of observed examples where (for example) a distorted image of a distant galaxy is seen as its light passes near a closer galaxy. The mass of these lensing galaxies inferred from reconstructing the path of the light is consistent with the dark matter halo mass and not just the visible mass.
The story is not completely settled, of course; maybe a modification of gravity can account for all of the above, although since very different distances scales are involved it is quite difficult to formulate such a theory. The more likely explanation is that dark matter exists, and the hunt is on to discover what it is!