Last time, we ended on finding the particular solution for the damped oscillator with simple oscillatory driving force:
\[ \begin{aligned} x_p(t) = \frac{F_0/m}{\sqrt{(\omega_0^2 - \omega^2)^2 + 4\beta^2 \omega^2}} \cos (\omega t - \delta). \end{aligned} \]
(Actually, this is assuming the force is also the real part of \( F(t) \) specifically. We'll go over this in detail shortly when we consider varying the phase of the driving.) So the particular contribution oscillates at the driving frequency \( \omega \), and its amplitude depends most strongly on the relative size of the driving frequency \( \omega \) to the natural frequency \( \omega_0 \).
Let's look at another special case to try to get a better feeling for this solution. Suppose that we're in the underdamped case, \( \beta < \omega_0 \). Then we can write the full solution with driving in the form
\[ \begin{aligned} x(t) = A \cos (\omega t - \delta) + A_1 e^{-\beta t} \cos (\omega_1 t - \delta_1) \end{aligned} \]
This is a little complicated-looking, but the second part of the solution is known as the transient; more important than the oscillation, it dies off exponentially as \( t \) increases. So although the short-time behavior will include both components, if we wait long enough, the transient term vanishes and we're just left with a simple oscillation at the driving frequency:
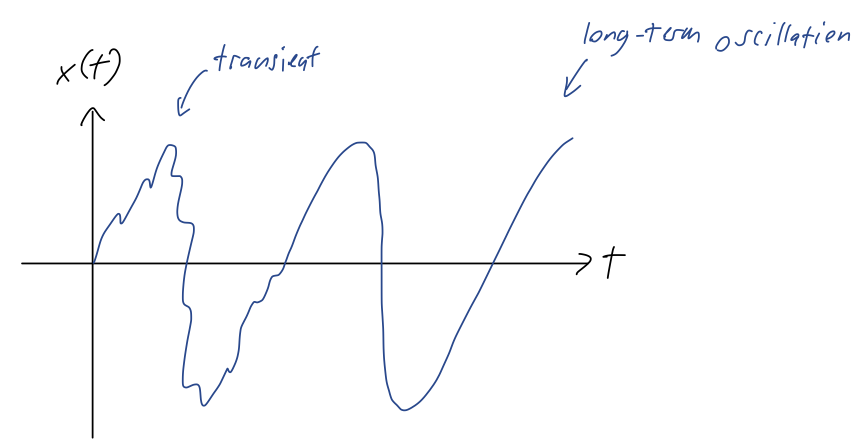
In fact, this is completely general: we know the critically damped and overdamped cases also die off exponentially with time, so those components are also transients. We find that no matter what \( \beta \) is, the long-term behavior of a driven damped oscillator is just simple oscillation at exactly the driving frequency.
Let's summarize what we've found. The key points to remember for sinusoidal (i.e. complex exponential) driving force \( F(t) = F_0 e^{i\omega t} \) are:
- The long-term behavior is oscillation of the form
\[ \begin{aligned} x(t) \rightarrow A \cos (\omega t - \delta) \end{aligned} \]
at exactly the same angular frequency \( \omega \) as the driving force. At shorter times there will be an additional transient behavior, with form depending on whether the system is over/underdamped.
- The motion of the system is phase shifted relative to the driving force, with phase shift given by
\[ \begin{aligned} \tan \delta = \frac{2\beta \omega}{\omega_0^2 - \omega^2}. \end{aligned} \]
- The amplitude of the system depends not just on the strength of the force, but also on the frequency of the driving, the natural frequency, and the damping constant:
\[ \begin{aligned} A = \frac{F_0/m}{\sqrt{(\omega_0^2 - \omega^2)^2 + 4\beta^2 \omega^2}}. \end{aligned} \]
This is actually a lot more general than it looks. In particular, we know that we can construct a more general periodic driving force by adding together \( \sin(\omega t) \) and \( \cos(\omega t) \) with arbitrary coefficients. But if we have a driving force that splits into parts, we can just add up the particular solutions for the same parts to get the overall particular solution. In other words, if
\[ \begin{aligned} F(t) = F_1(t) + F_2(t) \end{aligned} \]
then the particular solution is just
\[ \begin{aligned} x_p(t) = x_{p,1}(t) + x_{p,2}(t). \end{aligned} \]
Example: sinusoidal driving
A damped harmonic oscillator is driven by an oscillating sinusoidal force,
\[ \begin{aligned} F(t) = F_0 \sin (\omega t). \end{aligned} \]
What is the long-time behavior of the solution \( x(t) \), after the transients have died out?
We start by rewriting our sinusoidal force in terms of complex exponentials: we know that
\[ \begin{aligned} F_0 \sin (\omega t) = -\frac{iF_0}{2} \left[ e^{i \omega t} - e^{-i\omega t} \right]. \end{aligned} \]
We can think of this as a sum over two driving forces, one with \( c = +i \omega \) and the other with \( c = -i \omega \). Instead of using our general result for \( C_3 \) (which would be fine), let me take each of these and plug them in to the equation of motion,
\[ \begin{aligned} \ddot{x} + 2\beta \dot{x} + \omega_0^2 x = \frac{F_0}{m} e^{ct} \end{aligned} \]
we find first
\[ \begin{aligned} \left[ -\omega^2 + 2i\omega \beta + \omega_0^2 \right] C_{3,+} e^{i \omega t} = -\frac{iF_0}{2m} e^{i \omega t} \end{aligned} \]
which leads to
\[ \begin{aligned} C_{3,+} = \frac{-iF_0/m}{2(\omega_0^2 - \omega^2) + 4i\omega \beta}. \end{aligned} \]
For the other term, we have
\[ \begin{aligned} \left[ -\omega^2 - 2i\omega \beta + \omega_0^2 \right] C_{3,-} e^{-i \omega t} = \frac{iF_0}{2m} e^{-i \omega t} \end{aligned} \]
giving
\[ \begin{aligned} C_{3,-} = \frac{iF_0/m}{2(\omega_0^2 - \omega^2) - 4i \omega \beta}. \end{aligned} \]
The full particular solution comes from putting these together:
\[ \begin{aligned} x_p(t) = C_{3,+} e^{i \omega t} + C_{3,-} e^{-i \omega t} \\ = \frac{-iF_0}{2m} \left[ \frac{1}{(\omega_0^2 - \omega^2) + 2i\omega \beta} e^{i\omega t} - \frac{1}{(\omega_0^2 - \omega^2) - 2i\omega \beta} e^{-i\omega t} \right] \end{aligned} \]
Now, the quickest way to put these terms back together is to recognize that the second term is exactly just the complex conjugate of the first term. With \( z = x + iy \), we recognize that
\[ \begin{aligned} z-z^\star = x + iy - x + iy = 2iy = 2i\ {\rm Im}\ z \end{aligned} \]
so
\[ \begin{aligned} x_p(t) = \frac{F_0}{m} \ {\rm Im} \left[ \frac{1}{(\omega_0^2 - \omega^2) + 2i\omega \beta} e^{i\omega t} \right] \\ = \frac{F_0}{m} \ {\rm Im} \left[ A e^{-i \delta} e^{i\omega t} \right] \end{aligned} \]
where \( A \) and \( \delta \) are exactly the same values we found above. This time we end up with the imaginary part, which picks off sine instead of cosine:
\[ \begin{aligned} x_p(t) = A \sin (\omega t - \delta). \end{aligned} \]
If we had started with a cosine driving force, then we would end up with the real part here instead of the imaginary part (try going through the algebra if you need a bit of complex number practice!)
By the way, another way to get this result is to work in terms of phase shifts from the start. We know that
\[ \begin{aligned} \cos (\theta - \pi/2) = \sin (\theta) \end{aligned} \]
so we can think of the original force as just being phase-shifted. Let's consider the general case
\[ \begin{aligned} F(t) = F_0 \cos (\omega t - \delta_0) = F_0\ {\rm Re} [e^{i \delta_0} e^{i\omega t}] = \frac{F_0}{2} [e^{i(\omega t - \delta_0)} + e^{-i(\omega t - \delta_0)}]. \end{aligned} \]
where again \( F_0 \) is explicitly real and \( \delta_0 = \pi/2 \) would give us the sinusoidal force that we just found. As with the sine example above, the phase ends up in the numerator of \( C_3 \) for each part of the solution. For example, taking the first part of the expression gives
\[ \begin{aligned} [-\omega^2 + 2i\omega \beta + \omega_0^2] C_{3,+} e^{i\omega t} = \frac{F_0}{2m} e^{i \omega t} e^{-i\delta_0} \end{aligned} \]
and we have the phase in the numerator with an extra minus sign on it,
\[ \begin{aligned} C_{3,\pm} = \frac{F_0 e^{ \mp i\delta_0} / m}{2(\omega_0^2 - \omega^2) pm 4i \beta \omega}. \end{aligned} \]
Since \( e^{i\delta0} \) is a "pure phase", it won't change the amplitudes \( |C{3,\pm}| \) at all. When we go to put them together again to find the particular solution, we thus have
\[ \begin{aligned} x_p(t) = \frac{F_0}{2m} \left[ \frac{1}{(\omega_0^2 - \omega^2) + 2i \omega \beta} e^{i \omega t} e^{-i \delta_0} - \frac{1}{(\omega_0^2 - \omega^2) - 2i \omega \beta)} e^{-i\omega t} e^{+i\delta_0} \right] \\ = \frac{F_0}{m} \ {\rm Re} \left[ \frac{1}{(\omega_0^2 - \omega^2) + 2i \omega \beta} e^{i(\omega t - \delta_0)} \right] \\ = \frac{F_0}{m} A \cos (\omega t - \delta_0 - \delta), \end{aligned} \]
with \( A \) and \( \delta \) exactly as we found them before. So in other words, dealing with an arbitrarily phase-shifted driving force is very simple: the amplitude is the same no matter what the phase is, and the quantity
\[ \begin{aligned} \delta = \tan^{-1} \left( \frac{2\beta \omega}{\omega_0^2 - \omega^2} \right) \end{aligned} \]
is exactly the phase shift between the driving oscillator and the motion \( x(t) \) of the system (after transients have died off.)
Resonance
Now let's move on to talk about resonance, an interesting phenomenon which occurs in cases where the damping is relatively weak compared to both of the other frequencies, \( \beta \ll \omega, \omega_0 \). Resonance can be thought of as something which occurs when we vary the frequency and look at the amplitude of oscillations. Depending on the situation, this might be either varying \( \omega \) or \( \omega_0 \);
As we've referred to before, an LRC circuit is a common example of a damped oscillator. When a radio station broadcasts its signal, it does so at a fixed frequency \( \omega \) - the radio signal is the driving force in the LRC case. To listen to the radio, you tune your radio to change \( \omega_0 \), by adjusting the resistance or capacitance of your radio circuit. So in this case, \( \omega \) is fixed and we should think about changing \( \omega_0 \).
On the other hand, a real-world mechanical system like a bridge might have a certain natural frequency \( \omega_0 \) which is not easily adjusted. However, a person walking across the bridge provides a driving force with adjustable frequency \( \omega \). So now we think of \( \omega_0 \) as fixed and imagine changing \( \omega \).
From our formula for the amplitude
\[ \begin{aligned} A = \frac{F_0/m}{\sqrt{(\omega_0^2 - \omega^2)^2 + 4\beta^2 \omega^2}}. \end{aligned} \]
we know that changing \( \omega \) is a little more complicated than changing \( \omega_0 \), since \( \omega \) appears twice in the denominator. But for small enough \( \beta \), the behavior (i.e. the phenomenon of resonance) will be the same in both cases.
Let's think about the small-\( \beta \) limit, although we have to be careful with how we expand: we want to avoid actually taking \( \beta \) all the way to zero. As long as \( \beta^2 \) is small compared to either \( \omega^2 \) or \( \omega_0^2 \), we see that the second term underneath the square root is always very small. Meanwhile, the first term will also become small if we let \( \omega_0 \rightarrow \omega \). Once both terms are small, the overall amplitude will become very large - diverging, in fact, if we really try to set \( \beta = 0 \).
Let's factor out a \( 1/\omega^2 \) from everything, resulting in
\[ \begin{aligned} A = \frac{F_0/m}{\omega^2 \sqrt{(1 - \omega_0^2 / \omega^2)^2 + 4 \beta^2 / \omega^2 }}. \end{aligned} \]
Now we series expand as \( \omega_0 / \omega \rightarrow 1 \). As usual, this is easier if we change variables: let's say that \( \omega_0 = \omega + \delta \). Then
\[ \begin{aligned} (1 - \omega_0^2 / \omega^2)^2 = (1 - (1 - \delta/\omega)^2)^2 = (1 - 1 + 2\delta/\omega - \delta^2/\omega^2)^2 \approx 4\delta^2/\omega^2 \end{aligned} \]
discarding higher-order terms in \( \delta \). Then series expanding with the binomial formula gives
\[ \begin{aligned} A = \frac{F_0/m}{\omega \sqrt{4\delta^2 + 4\beta^2}} \\ = \frac{F_0}{2\omega m} \left( \frac{1}{\beta} - \frac{\delta^2}{2\beta^3} + ...\right) \end{aligned} \]
So close to \( \omega_0 = \omega \), we have a local maximum amplitude of \( A = F_0 / (2m \omega \beta) \). Near this maximum, as we change \( \omega_0 \) slightly away from \( \omega \), the amplitude decreases quadratically. In fact, it's easy to see that this peak is the global maximum: any value of \( \omega_0 \) different from \( \omega \) gives a positive contribution to the denominator and makes \( A \) smaller.
Moving away from the peak, we see furthermore that as \( \omega_0 \rightarrow 0 \) the amplitude goes to a finite value,
\[ \begin{aligned} A(\omega_0 \rightarrow 0) \rightarrow \frac{F_0/m}{\omega^2 \sqrt{1 + 4\beta^2 / \omega^2}} \approx \frac{F_0}{m \omega^2} \end{aligned} \]
using the fact that we're in the weak-damping limit so \( \beta / \omega \) is small. This also tells us that this value of \( A \) is much smaller than the peak, again by one power of \( \beta / \omega \). Finally, going to large natural frequency, the \( \omega_0^4 \) term eventually dominates everything else, and we find
\[ \begin{aligned} A(\omega_0 \rightarrow \infty) \rightarrow \frac{F_0}{m \omega_0^2}, \end{aligned} \]
which dies off to zero as \( \omega_0 \) gets larger and larger. Now we have all the information we need to make a sketch of amplitude vs. natural frequency:
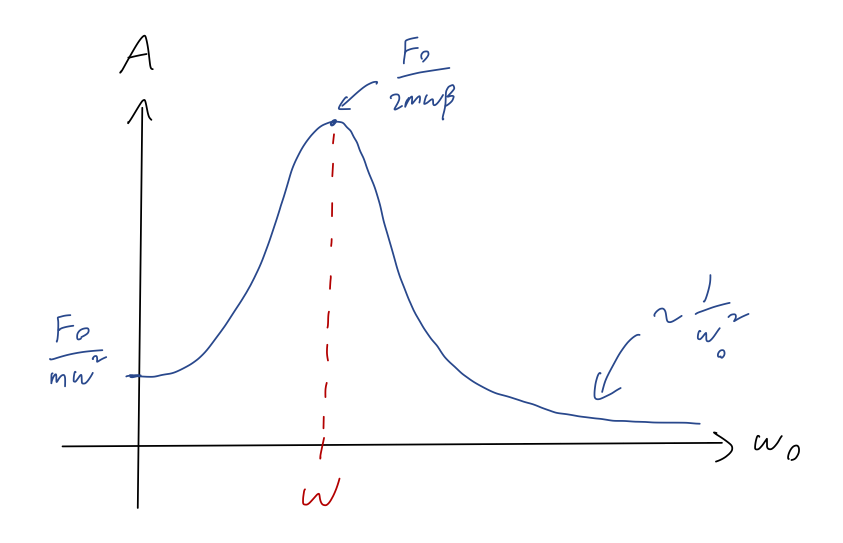
The large peak in the amplitude is called a resonance. Basically, we obtain a huge increase in the amplitude of oscillations as we tune the natural frequency \( \omega_0 \) close to the driving frequency \( \omega \). This effect is stronger when \( \beta \) is small: as \( \beta \) decreases, the peak amplitude becomes larger and the resonance becomes sharper (the width decreases.)
Now let's briefly consider the alternative situation, where \( \omega_0 \) is fixed and we are instead adjusting the driving frequency \( \omega \). This will be a lot messier if we try to series expand, but we know that we expect the same qualitative behavior: as the term \( \omega_0 - \omega \) vanishes in the denominator, the amplitude will become very large as long as the second term including \( \beta \) is relatively small. Instead of doing the full series expansion, let's use a derivative to find the position of the resonance peak. It will be easier to work with the squared amplitude for this:
\[ \begin{aligned} |A|^2 = \frac{F_0^2/m^2}{(\omega_0^2 - \omega^2)^2 + 4\beta^2 \omega^2} \end{aligned} \]
(it should be clear that the maximum of \( |A| \) is also the maximum of \( |A|^2 \).) We can take a derivative of the whole thing to find extrema, but maximizing \( |A|^2 \) is the same thing as minimizing the denominator alone, so let's just work with that directly:
\[ \begin{aligned} \frac{d}{d\omega} \left[ (\omega_0^2 - \omega^2)^2 + 4\beta^2 \omega^2 \right] = -4 \omega (\omega_0^2 - \omega^2) + 8\beta^2 \omega = 0 \end{aligned} \]
This has a solution at \( \omega = 0 \), but we know already that's not the right answer for the resonance peak. Dividing out the overall \( \omega \) leaves us with a quadratic equation,
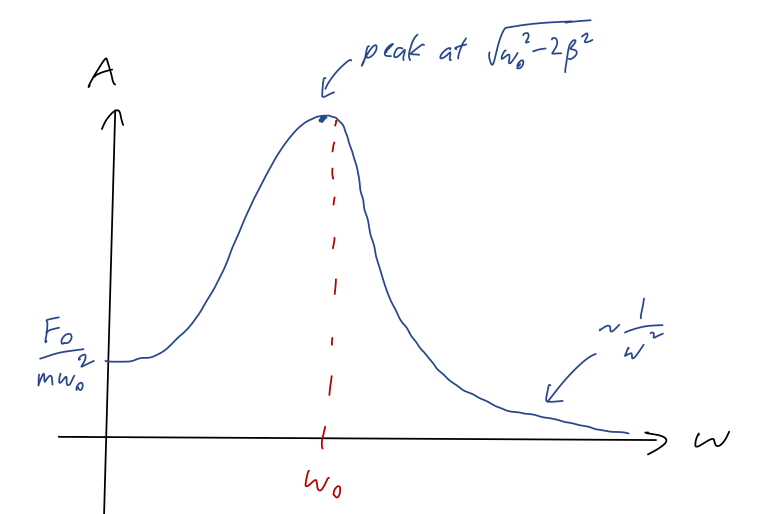
\[ \begin{aligned} 4 \omega^2 - 4\omega_0^2 + 8 \beta^2 = 0 \\ \omega = \sqrt{\omega_0^2 - 2\beta^2} \end{aligned} \]
taking the positive root since \( \omega \) has to be positive. This is close to \( \omega_0 \) for small \( \beta \), so this is definitely the location of the resonance peak! We notice that in this case, there's actually a small offset: the peak as a function of \( \omega \) is slightly to the left of \( \omega = \omega_0 \). Let's make another sketch - I've noted the behaviors at small and large \( \omega \) as well, which I leave up to you to double-check:
If we plug back in the peak value into the amplitude formula, we find
\[ \begin{aligned} A = \frac{F_0/m}{\sqrt{(\omega_0^2 - (\omega_0^2 - 2\beta^2))^2 + 4\beta^2 (\omega_0^2 - 2\beta^2)}} \\ = \frac{F_0/m}{\sqrt{4 \beta^2 (\omega_0^2 - \beta^2)}} \approx \frac{F_0}{2m\omega_0 \beta} \end{aligned} \]
neglecting the extra term proportional to \( (\beta/\omega_0)^2 \). This is the same as in the case where we varied \( \omega_0 \).