Rectangular coordinates, continued; vector products
Continuing from last time, let's pick up on rectangular coordinates \( (x,y,z) \).
At this point, it's good to introduce vector notation, which will be very helpful in thinking about relating different coordinate systems. We define three unit vectors \( \hat{x}, \hat{y}, \hat{z} \) which point along the corresponding axes. Then we can write any other vector in terms of the unit vectors. For example, the position vector \( \vec{r} \) describes the location of an object relative to the origin:
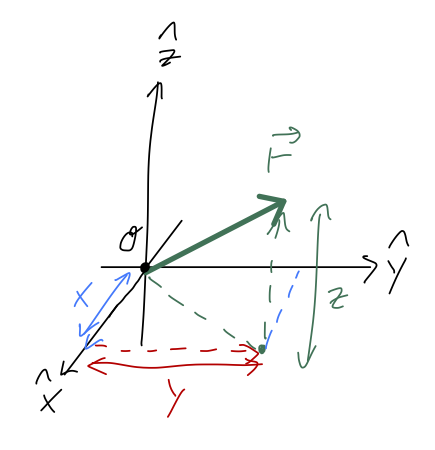
\[ \begin{aligned} \vec{r} = x \hat{x} + y \hat{y} + z \hat{z} \end{aligned} \]
Common alternative names for the unit vectors are \( \hat{i}, \hat{j}, \hat{k} \) and \( \hat{e}_1, \hat{e}_2, \hat{e}_3 \); the latter generic-looking set are sometimes used to describe other coordinate systems, so beware!
(Notation aside: I will use arrows to denote vectors; Taylor uses bold-face, so he would write the vector above as \( \mathbf{r} \). Bold-face is hard to use when you're writing by hand!)
As mentioned above, keeping track of units is very important, so when we introduce new things I'll try to mention their dimensions as well. Since \( \vec{r} \) has units of distance, and so do the individual lengths \( x,y,z \), we notice that _the unit vectors themselves have no units_ - they just point in a direction.
When we want to refer to components of a vector by name, we'll use a subscript equal to the corresponding unit vector: for example, if \( \vec{v} \) is a velocity, then \( v_x \) is the speed in the x-direction. For the position vector,
\[ \begin{aligned} r_x = x \end{aligned} \]
Vector information about an object and its motion is great, but often we want to know things like: "what is the speed of my object?" or "how far are these two masses from each other?" Speed and distance are examples of scalar information: they are quantities that don't care about direction, which means they definitely aren't vectors! A useful idea to get scalar information from vector information is the dot product, which multiplies two vectors together component by component and gives back a number:
\[ \begin{aligned} \vec{a} \cdot \vec{b} = a_x b_x + a_y b_y + a_z b_z \end{aligned} \]
We can immediately use this to define useful things. For example, the dot product of a vector with itself gives us the square of its length, just by the Pythagorean theorem:
\[ \begin{aligned} |\vec{r}| = \sqrt{ x^2 + y^2 + z^2} = \sqrt{\vec{r} \cdot \vec{r}} \end{aligned} \]
where paired vertical lines \( |...| \) gives absolute value for a regular number, but length for a vector. They're sort of the same thing, because a vector's length can't be negative, and it's easy to show that \( |-\vec{r}| = |\vec{r}| \). When it isn't ambiguous, I'll usually write this simply as \( r = |\vec{r}| \).
In general, if you go look up some trigonometry formulas, it's not too hard to show that
\[ \begin{aligned} \vec{a} \cdot \vec{b} = ab \cos \theta, \end{aligned} \]
where \( \theta \) is the angle between the two vectors. I won't derive this formula, but I will apply one other concept that I'll emphasize over and over, which is checking limits and special cases (another technique to save you from hours of frustration!) First special case: if \( \vec{b} = \vec{a} \), then the angle \( \theta \) is obviously zero, and we recover the formula \( \vec{a} \cdot \vec{a} = |\vec{a}|^2 \) from above. Our check is successful!
Another interesting limit is when \( \theta = 90^\circ \): the formula tells us that the dot product should be \( ab \cos 90^\circ = 0 \). If we pick our coordinates axes so that \( \vec{a} = a \hat{x} \) and \( \vec{b} = b \hat{y} \), for example, then it's easy to confirm this from the definition. So this check passes too.
A natural question you might ask is: what if I've already picked my coordinate axes, and my vectors \( \vec{a} \) and \( \vec{b} \) aren't along the coordinate axes? Why does the argument above still work? A really important point to remember is that vectors exist independent of our choice of coordinates. Mathematically, this is true by definition: obviously in physics, it had better be true, because a block sliding down a ramp only has a single velocity vector even if you and I measure it differently.
Since \( \vec{a} \cdot \vec{b} \) only depends on the vectors and not on any components, it is coordinate-independent. This is why I was allowed to pick my coordinates above to work out what happens to the dot product when \( \theta = 90^\circ \).
We emphasized that unit vectors like \( \hat{x} \) just point in a direction: they carry no units and their length doesn't change. Using the dot product, we can define a unit vector pointing in the direction of any vector by dividing its length out:
\[ \begin{aligned} \hat{a} = \frac{1}{\sqrt{(\vec{a} \cdot \vec{a})}} \vec{a}. \end{aligned} \]
or using our informal notation for the length and inverting, \( \vec{a} = a \hat{a} \). As another example, we can write the position vector as \( \vec{r} = r \hat{r} \).
The other important vector product to know is the cross product, \( \vec{a} \times \vec{b} \). However, it will be a while until we actually have a use for it this semester, so I'll defer talking about it until later on.
Cylindrical coordinates
I'll do cylindrical coordinates next, because they only swap out two out of three coordinates from Cartesian coordinates: \( \hat{z} \) is kept the same. Ignoring the \( z \)-direction, we want to swap out the other two coordinates \( (x,y) \) for 2-d polar coordinates:
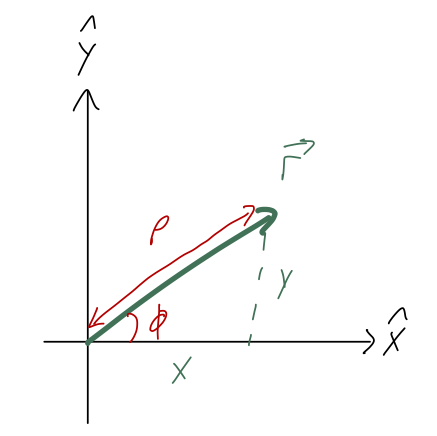
(Note: Taylor does something I think is confusing, which is to use \( r \) instead of \( \rho \) if he's in two dimensions. I'll always use \( \rho \) for the polar radius, keeping \( r \) for the three-dimensional position vector, i.e. distance to the origin. If \( z=0 \), then these are the same.)
As we can read off the sketch, the relationship between the coordinates is
\[ \begin{aligned} x = \rho \cos \phi \\ y = \rho \sin \phi \end{aligned} \]
or going backwards,
\[ \begin{aligned} \rho = \sqrt{x^2 + y^2} \\ \tan \phi = \frac{y}{x}. \end{aligned} \]
A word of warning about this last formula: you might be tempted to just use an inverse function to "simplify" it and write \( \phi = \tan^{-1} (y/x) \). The problem with this will be obvious if we plot the \( \tan^{-1} \) function:
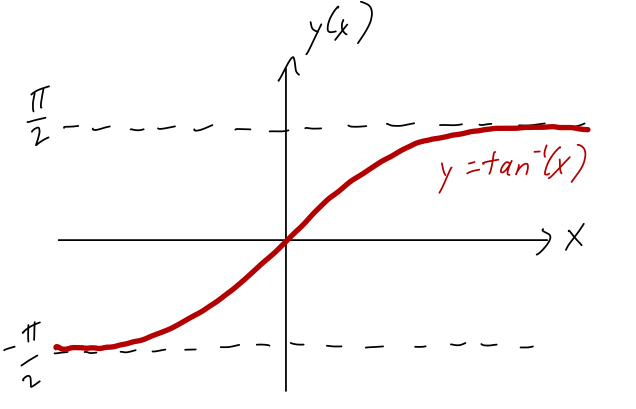
The range of \( \tan^{-1} \), i.e. its set of possible output values, is \( (-\pi/2, \pi/2) \). But this only covers half of the plane! The issue is that if we reflect a point from \( (x,y) \rightarrow (-x,-y) \), the value of the ratio \( y/x \) doesn't change: in terms of angles, \( \tan (\phi + \pi) = \tan \phi \). So if you use the ratio \( y/x \) to find what the coordinate \( \phi \) is, double-check what quadrant your point is supposed to be in!
If you're doing this numerically, it's not hard to write a computer program that will use \( \tan^{-1} \) and then check the signs and add \( \pi \) if needed. However, the program needs to know both \( x \) and \( y \) separately. In Mathematica, if you give two numbers i.e. ArcTan[x,y], it gives you exactly this corrected result for \( \phi \). In other programming languages, the 'quadrant-aware' version of the function is usually called arctan2.
If we want to do integrals in cylindrical coordinates, we need the volume element dV.
Clicker Question
What is the volume element \( dV \) in cylindrical coordinates?
A. \( dV = d\rho\ d\phi\ dz \)
B. \( dV = \rho\ d\rho\ d\phi\ dz \)
C. \( dV = \rho^2\ d\rho\ d\phi\ dz \)
D. \( dV = \sin \phi\ d\rho\ d\phi\ dz \)
E. \( dV = \rho \sin \phi\ d\rho\ d\phi\ dz \)
Answer: B
First of all, this is a good opportunity to drive home the point that checking units is a good idea! We can use the fact that the units of \( dV \) are \( [L]^3 \) to greatly narrow our choices: since the angle \( \phi \) is dimensionless, the only answers that have the correct dimensions are B and E.
To derive the infinitesmal volume element, we should start with a sketch of the small slice of physical space which is "swept out" if we move by a differential amount in each of the three available directions:
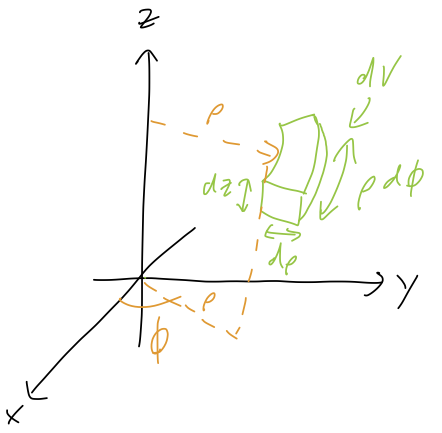
Note that sweeping in angle gives the distance element \( \rho\ d\phi \) as drawn - once again, paying attention to units! Multiplying the three sides together gives answer B. (You may object that this is a weird shape and not a cube, so we can't just multiply the sides together. But if \( d\phi \) is small enough, the volume element becomes close enough to a cube to use the usual formula. Try to visualize it by taking \( r \) bigger holding \( d\phi \) fixed.)
There is an algebraic way to derive the volume element instead, but it's not quite as simple as it looks at first. Since we know the change of coordinates from Cartesian and we know that \( dV = dx dy dz \), you might think that we could just compute \( dx \) and \( dy \) in terms of \( d\rho \) and \( d\phi \) and plug back in. If you try this, you'll find that it fails!
The problem is apparent from the picture above: because we're computing a volume, we have to account for the fact that \( dx \) and \( dy \) point in different directions than \( d\rho \) and \( d\phi \). In fact, the proper formula for the infinitesmal volume element is actually the triple product
\[ \begin{aligned} dV = (\vec{dx} \times \vec{dy}) \cdot \vec{dz}. \end{aligned} \]
Since all of the axes are perpendicular in Cartesian coordinates, this just becomes simply \( dx dy dz \). But in the current example, the difference matters; if you keep track of things properly, using this formula as the starting point should yield the correct cylindrical \( dV \).
On to the unit vectors. Remember that the idea of a coordinate unit vector is that it points in the direction in which that coordinate increases. But now, if we choose a couple of points and identify \( \hat{\rho} \) and \( \hat{\phi} \), it's easy to see that we have a new complication: the directions \( \hat{\rho} \) and \( \hat{\phi} \) depend on what point we are asking about!
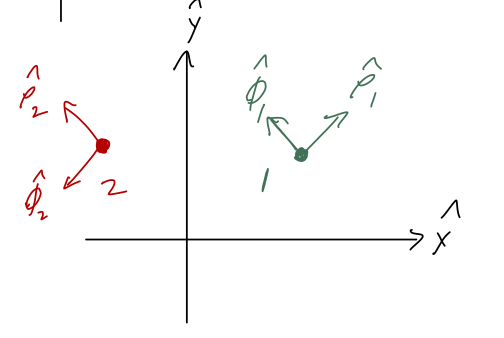
We can do a bit of trigonometry on any given point and easily show the general relationship
\[ \begin{aligned} \hat{\rho} = \cos \phi \hat{x} + \sin \phi \hat{y} \\ \hat{\phi} = -\sin \phi \hat{x} + \cos \phi \hat{y} \end{aligned} \]
The way in which they depend on our coordinates isn't so bad: their directions just change with the angle \( \hat{\phi} \).
Instead of going through the geometry, I'll show you an algebraic way to derive the unit vectors instead. When we take the derivative of a vector \( \vec{v} \) with respect to some other variable \( s \), the new vector \( d\vec{v}/ds \) gives us both the rate and the direction of change with respect to \( s \). So converting our words "unit vector pointing in the direction in which a coordinate increases" into equations,
\[ \begin{aligned} \hat{\rho} = \frac{d\vec{r}/d\rho}{|d\vec{r}/d\rho|} \\ \hat{\phi} = \frac{d\vec{r}/d\phi}{|d\vec{r}/d\phi|}. \end{aligned} \]
Next time, we'll see how these expressions lead to the unit vector formulas above.