Last time, I set up the idea that we can derive the cylindrical unit vectors \( \hat{\rho}, \hat{\phi} \) using algebra. Let's continue and do just that.
Once again, when we take the derivative of a vector \( \vec{v} \) with respect to some other variable \( s \), the new vector \( d\vec{v}/ds \) gives us both the rate and the direction of change with respect to \( s \). So converting our words "unit vector pointing in the direction in which a coordinate increases" into equations,
\[ \begin{aligned} \hat{\rho} = \frac{d\vec{r}/d\rho}{|d\vec{r}/d\rho|} \\ \hat{\phi} = \frac{d\vec{r}/d\phi}{|d\vec{r}/d\phi|}. \end{aligned} \]
We start by writing \( \vec{r} \) out in Cartesian components, ignoring \( \hat{z} \):
\[ \begin{aligned} \vec{r} = x\hat{x} + y\hat{y} \end{aligned} \]
Next, we substitute in the formulas for \( x \) and \( y \) in terms of cylindrical coordinates:
\[ \begin{aligned} \vec{r} = \rho \cos \phi \hat{x} + \rho \sin \phi \hat{y} \end{aligned} \]
Now we can take derivatives, remembering that the derivative of a vector is still a vector:
\[ \begin{aligned} \frac{d\vec{r}}{d\rho} = \cos \phi \hat{x} + \sin \phi \hat{y} \end{aligned} \]
and
\[ \begin{aligned} \frac{d\vec{r}}{d\phi} = -\rho \sin \phi \hat{x} + \rho \cos \phi \hat{y} \end{aligned} \]
These are the correct directions for \( \hat{\rho} \) and \( \hat{\phi} \) already; to make them unit vectors, we just have to normalize. It's easy to show that \( d\vec{r}/d\rho \) is already a unit vector, while the length of the other vector is
\[ \begin{aligned} \left| \frac{d\vec{r}}{d\phi} \right| = \sqrt{\rho^2 (\sin^2 \phi + \cos^2\phi)} = \rho. \end{aligned} \]
So finally, we have
\[ \begin{aligned} \hat{\rho} = \frac{d\vec{r}/d\rho}{|d\vec{r}/d\rho|} = \cos \phi \hat{x} + \sin \phi \hat{y} \\ \hat{\phi} = \frac{d\vec{r}/d\phi}{|d\vec{r}/d\phi|} = -\sin \phi \hat{x} + \cos \phi \hat{y} \end{aligned} \]
matching the result above.
Let's get a bit of practice with using these cylindrical unit vectors.
Clicker Question
Which is the correct decomposition of the position vector \( \vec{r} \) for the point \( (x,y) = (1,1) \)?
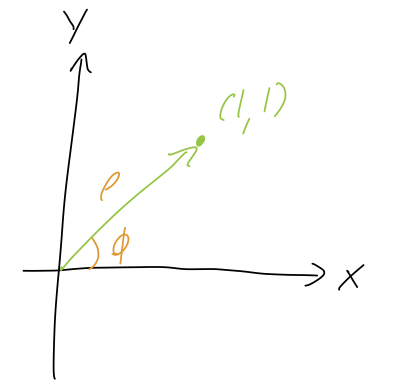
A. \( \vec{r} = \sqrt{2} \hat{\rho} \)
B. \( \vec{r} = \sqrt{2} \hat{\rho} + \frac{\pi}{4} \hat{\phi} \)
C. \( \vec{r} = \sqrt{2} \hat{\rho} - \frac{\pi}{4} \hat{\phi} \)
D. \( \vec{r} = \frac{\pi}{4} \hat{\phi} \)
Answer: A
The simplest way to understand this is by drawing the unit vectors on the sketch. You can do this just by geometric reasoning (the directions that \( \rho \) and \( \phi \) increase), or use our formulas above to find
\[ \begin{aligned} \hat{\rho} = \frac{1}{\sqrt{2}} (\hat{x} + \hat{y}) \\ \hat{\phi} = \frac{1}{\sqrt{2}} (-\hat{x} + \hat{y}) \end{aligned} \]
with either method leading to the following diagram:
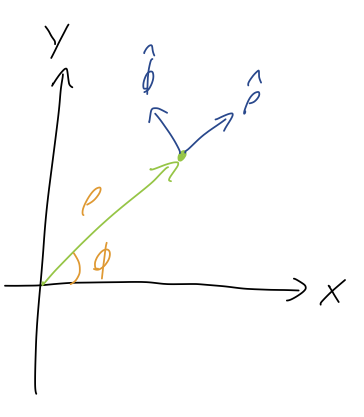
We see that \( \vec{r} \) is pointing directly along the \( \hat{\rho} \) direction, so it has no \( \hat{\phi} \) component - the answer is A. Yes, this means that if we pick any point in the plane, the vector \( \vec{r} \) never has any \( \hat{\phi} \) component! All of the points on the circle of radius \( \sqrt{2} \) from the origin have unit vector \( \vec{r} = \sqrt{2} \hat{\rho} \). The angular dependence is hidden within \( \hat{\rho} \) itself.
As the example above strongly hints, it's easy to show that the general expression for the position vector in cylindrical coordinates is
\[ \begin{aligned} \vec{r} = \rho \hat{\rho} + z \hat{z} \end{aligned} \]
with no \( \hat{\phi} \) component! If you are ever tempted to add a \( \phi \hat{\phi} \) term, you should be stopped by noticing it has the wrong units; \( \vec{r} \) should have units of distance, but \( \phi \) is unitless and so is \( \hat{\phi} \), so something is wrong with \( \phi \hat{\phi} \).
It's also very important to point out that in cylindrical coordinates, the decomposition of a vector depends on what point it starts at. If we took the same vector \( \hat{x} + \hat{y} \) and started it at the point \( (1,-1) \), now it is pointing purely in the \( \hat{\phi} \) direction! We'll mostly be dealing with vectors from the origin like \( \vec{r} \), in which case this won't be an issue, but I wanted to point it out anyway so you're aware.
Spherical coordinates
In spherical coordinates, we adopt \( r \) itself as one of our coordinates, in combination with two angles that let us rotate around to any point in space. We keep the angle \( \phi \) in the x-y plane, and add the angle \( \theta \) which is taken from the positive \( \hat{z} \)-axis:
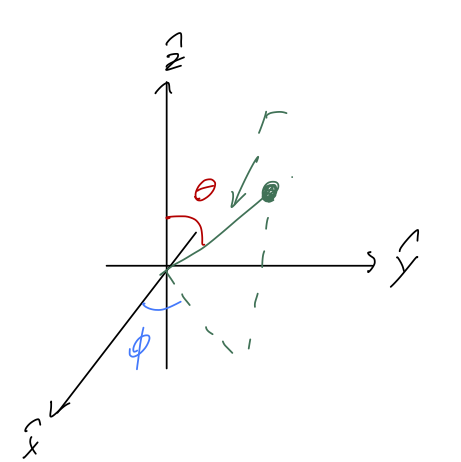
(Confusingly, \( \theta \) is usually called the "polar angle", thinking of the z-axis as the "pole". In this case, \( \phi \) is called the "azimuthal angle". See Taylor, p.135.)
Important note: these are the physics conventions for what to call these angles. Mathematicians tend to prefer the opposite choice, using \( \theta \) as the azimuthal angle and \( \phi \) the polar. Math books (and some physics texts) will also use \( \rho \) for the spherical distance and \( r \) the polar distance. Be very careful when looking at other resources!
The relationship between spherical and cylindrical coordinates is actually relatively simple to work out, as we can see by looking at a cross-section containing both \( \vec{r} \) and \( \hat{z} \):
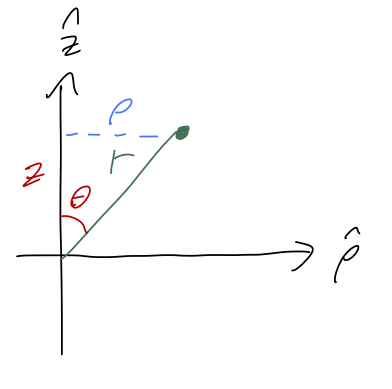
It's easy to see from the sketch that
\[ \begin{aligned} z = r \cos \theta \\ \rho = r \sin \theta \end{aligned} \]
We can then take this and plug in one more step to get the formulas for rectangular coordinates:
\[ \begin{aligned} x = r \sin \theta \cos \phi \\ y = r \sin \theta \sin \phi \\ z = r \cos \theta \end{aligned} \]
If you forget exactly where the sine and cosines go in this expression, I find it's easiest to think about converting from cylindrical coordinates. I'll skip the derivation of the volume element since it's more involved, but the result is important for doing integrals:
\[ \begin{aligned} dV = r^2 \sin \theta\ dr\ d\theta\ d\phi. \end{aligned} \]
Clicker Question
In spherical coordinates, if we want to integrate over a sphere of radius \( R \) centered at the origin, what are the correct limits of integration?
A. \( r \): 0 to \( R \), \( \theta \): 0 to \( \pi \), \( \phi \): 0 to \( 2\pi \).
B. \( r \): 0 to \( R \), \( \theta \): 0 to \( 2\pi \), \( \phi \): 0 to \( 2\pi \).
C. \( r \): \( -R \) to \( R \), \( \theta \): 0 to \( 2\pi \), \( \phi \): 0 to \( \pi \).
D. \( r \): \( -R \) to \( R \), \( \theta \): 0 to \( 2\pi \), \( \phi \): 0 to \( 2\pi \).
Answer: A
Here we have to be careful about ambiguities in what we call a certain point. Let's hold \( r \) fixed for a moment and just think about the angles. If we let \( \phi \) run from \( 0 \) to \( 2\pi \), it will trace out a circle around the \( \hat{z} \)-axis. If we now let \( \theta \) start to vary as well, we will trace out a family of circles that will build up the surface of a sphere.
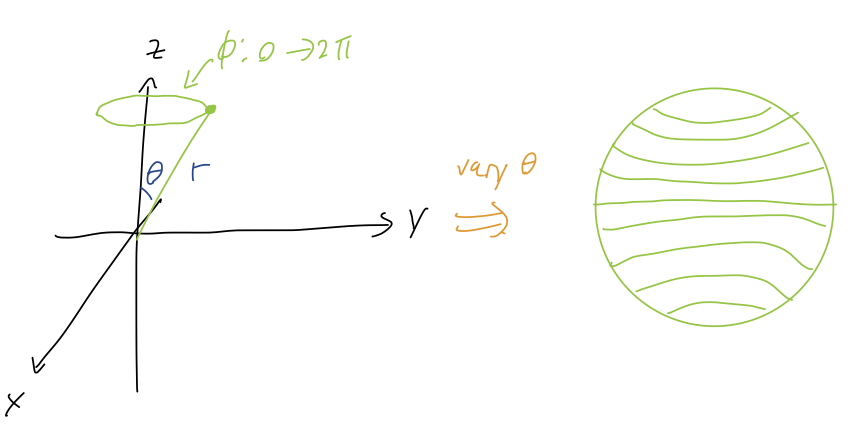
However, we have a new ambiguity when we work with circles: \( \theta \) and \( -\theta \) both trace out the same circle. This means that we can't let \( \theta \) vary all the way from \( 0 \) to \( 2\pi \), or we'll be double-counting: it has to run only from \( 0 \) to \( \pi \).
The same ambiguity applies to \( r \). Usually by convention we define \( r \) to be only positive, but a negative \( r \) will work just fine in the coordinate system we've defined. However, the point \( (-r, \theta, \phi) \) is equivalent to a rotation of the point \( (r, \theta, \phi) \). To be precise, it's easy to show that
\[ \begin{aligned} (-r, \phi, \theta) = (r, \phi + \pi, \pi - \theta). \end{aligned} \]
So the range from \( -R \) to \( 0 \) will produce the same spherical shells as \( 0 \) to \( R \) when we integrate over the angles. Thus, we should skip the negative \( r \) values and we arrive at option A.
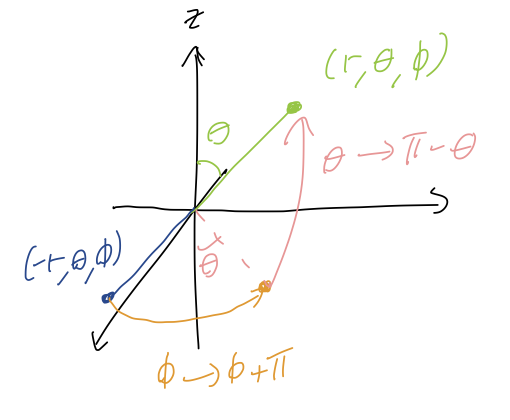
(Bonus material: If you've been paying really close attention, you might wonder if option C would work if it had \( r \) from \( 0 \) to \( R \). Can't we just switch the angles \( \theta \) and \( \phi \) in our "spherical shell" argument above, so that it will work as long as one of them goes to \( 2\pi \) and one goes to \( \pi \)? The answer is no, but it's a very subtle point that has to do with exactly how we defined our angles. The "same circle" ambiguity above is really the statement that
\[ \begin{aligned} (r, \phi, -\theta) = (r, \phi+\pi, +\theta) \end{aligned} \]
i.e. we can undo a reflection \( \theta \rightarrow -\theta \) by rotating around in the \( \phi \) direction by \( \pi \). However, the converse statement is not true:
\[ \begin{aligned} (r, -\phi, \theta) \neq (r, +\phi, \theta + \pi). \end{aligned} \]
In fact, changing \( \theta \) doesn't change \( \phi \) at all, except that it can flip it to \( \phi + \pi \) if we go to the other side of the axis. So there is no way to get to \( -\phi \) from \( +\phi \) by changing \( \theta \).)
We could find results for the unit vectors in spherical coordinates \( \hat{\rho}, \hat{\theta}, \hat{\phi} \) in terms of the Cartesian unit vectors, but we're not going to be doing vector calculus in these coordinates for a while, so I'll put this off for now - it's a bit messy compared to cylindrical.
Motion and Newton's laws
Now that we've set up our coordinate system basics, let's turn back to physics, starting with Newton's laws of motion. Taylor discusses some fundamentals about defining mass and force, but I'll let you read that on your own. First, let's remind ourselves what Newton's three laws of motion are in words:
- In the absence of forces, an object moves with constant velocity.
- An object of mass \( m \) subject to a net force will accelerate according to the relation
\[ \begin{aligned} \vec{F} = m \vec{a}. \end{aligned} \]
- If object 1 exerts a force on object 2, there is an equal and opposite force exerts on object 2 by object 1,
\[ \begin{aligned} \vec{F}_{12} = -\vec{F}_{21}. \end{aligned} \]
In our modern understanding, the first law is more or less redundant, because the second law immediately tells us that if \( \vec{F} = 0 \), then \( \vec{a} = 0 \); since \( \vec{a} = d\vec{v}/dt \), no acceleration means constant velocity. (This isn't quite true, because you can think of the first law as something to check to make sure you're in an inertial frame where the second law will hold; see the discussion in Taylor, chapter 1. More on inertial frames in a bit.)
We mentioned vector derivatives before, but let's talk a bit more about them, and time derivatives specifically. Backing up a step, the velocity vector is the time derivative of the position vector,
\[ \begin{aligned} \vec{v} = \frac{d\vec{r}}{dt} \end{aligned} \]
We can think about the meaning of this expression by unpacking it using unit vectors and the product rule:
\[ \begin{aligned} \frac{d}{dt} \vec{r} = \frac{d}{dt} \left( x \hat{x} + y \hat{y} + z \hat{z} \right) \\ = \frac{dx}{dt} \hat{x} + \frac{dy}{dt} \hat{y} + \frac{dz}{dt} \hat{z} \\ = \dot{x} \hat{x} + \dot{y} \hat{y} + \dot{z} \hat{z}. \end{aligned} \]
Here I introduce some new notation, since we'll be taking lots and lots of time derivatives: a dot over a quantity indicates acting on it with \( d/dt \),
\[ \begin{aligned} \dot{q} \equiv \frac{dq}{dt}. \end{aligned} \]
(Bonus notation: \( \equiv \) is the equivalence symbol and means "is defined to be".) This applies both to scalars and vectors, so for example we can write \( \vec{v} = \dot{\vec{r}} \). Finally, multiple dots can be used for multiple derivatives, so Newton's second law can be written out as
\[ \begin{aligned} \vec{F} = m \vec{a} = m \frac{d^2 \vec{r}}{dt^2} = m \ddot{\vec{r}}. \end{aligned} \]
Since we just looked at the decomposition of \( \dot{\vec{r}} \) in Cartesian coordinates, let's look at Newton's second law in the same coordinates. Taking another time derivative will just give us double-dots instead of single-dots on the right side of the equation, so we have:
\[ \begin{aligned} F_x \hat{x} + F_y \hat{y} + F_z \hat{z} = m \left(\ddot{x} \hat{x} + \ddot{y} \hat{y} + \ddot{z} \hat{z} \right) \end{aligned} \]
This is, in fact, just three separate copies of the same equation, one for each direction:
\[ \begin{aligned} F_x = m\ddot{x} \\ F_y = m\ddot{y} \\ F_z = m\ddot{z} \end{aligned} \]
Although it's usually taken as obvious, you might ask at this point why we're allowed to break one equation up into three. Because this is a vector equation, and two vectors will only be equal if all of their components are equal, we can just check one component at a time. Of course, that means that we have a system of equations, which must all be true at once. These equations are collectively known as the equations of motion, because if we solve them, we know the answer for \( \vec{r}(t) \) - we know what the motion of the system will look like over time.
Example: block on a ramp and coordinate choices
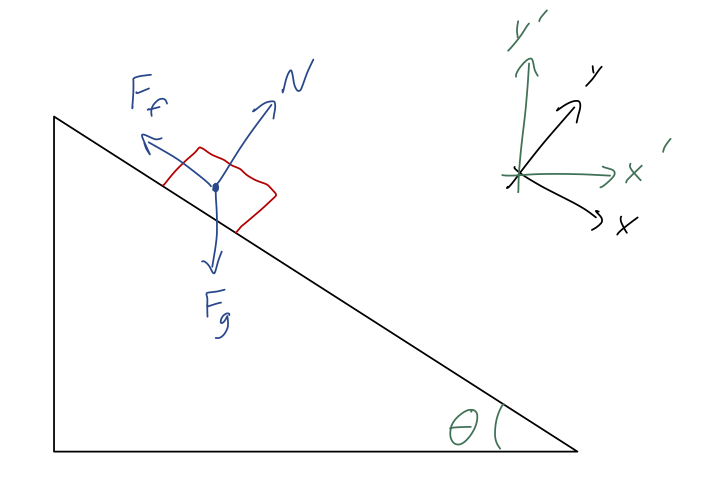
Taylor does this as his example 1.1, but he takes his \( x \)-axis to be parallel to the ramp. To get used to comparing different coordinate systems, I'll instead set my \( y \)-axis to be in the direction of gravity - I'll call this the \( y' \) axis. As Taylor points out, this will make things slightly more complicated, but it's not too bad. We'll treat this as a two-dimensional problem, as indicated, which just means that we ignore the \( z \) coordinate. (This is valid because of Newton's first law: if there are no \( z \)-direction forces, then there is no interesting \( z \)-direction motion at all.)
We'll continue with this example next time.