The first example I will consider here is the simplest, which is horizontal motion with linear drag. (You can realize this experimentally by immersing a frictionless cart on a surface in some viscous liquid, like honey or molasses.) If we just start the cart off with some initial speed \( v_0 \) and release it, the only force acting will be drag:

Newton's second law is thus
\[ \begin{aligned} m \ddot{x} = -b \dot{x}. \end{aligned} \]
As I said a little while back, we can turn this into a first-order ODE by taking \( v_x = \dot{x} \) as our unknown variable, leading to the equation
\[ \begin{aligned} \dot{v}_x = -\frac{b}{m} v_x. \end{aligned} \]
Clicker Question
_Without solving the equation, assuming that \( v_x(t=0) = v0 > 0 \), what can we tell about the behavior of this system at long times?
A. The cart will accelerate forever (\( v_x \) increases without bound.)
B. The cart will slow down to reach a constant "terminal" velocity \( v_t > 0 \).
C. The cart will slow down to a stop (\( v_x \) goes to zero.)
D. The cart will oscillate back and forth, never stopping, with \( v_x \) changing sign repeatedly.
Answer: C
Let's look closely at what the equation is telling us. First of all, the minus sign means that \( dv_x / dt \) has the opposite sign of \( v_x \), which means that it will tend to push \( v_x \) closer to zero (also true if we had \( v_0 < 0 \).) So we can definitely rule out A - which you probably knew just based on physical intuition anyway. This also rules out D: because the derivative always pushes \( v_x \) towards zero, there is no way for the system to go past zero.
How do we decide between B and C? We can easily test these situations out by using the equation. Suppose that B is right, and there is a terminal velocity \( v_t > 0 \). If we plug that speed in to the equation, we find
\[ \begin{aligned} \frac{dv_x}{dt} = -\frac{b}{m} v_t < 0. \end{aligned} \]
But this means that \( v_x \) will decrease for any possible value of \( v_t \), and if \( v_x \) is still changing, then it can't be a "terminal" velocity! On the other hand, case C works just fine: if we have \( v_x = 0 \), then the differential equation becomes
\[ \begin{aligned} \frac{dv_x}{dt} = 0 \end{aligned} \]
and the system stays at zero speed forever.
Now let's find the solution. This is a separable ODE, so we can solve it right away. Separating \( v_x \) and \( t \) out gives
\[ \begin{aligned} \frac{dv_x}{v_x} = -\frac{b}{m} dt \end{aligned} \]
and then integrating leads to
\[ \begin{aligned} \ln v_x = -\frac{bt}{m} + C \Rightarrow v_x(t) = C' e^{-bt/m} \end{aligned} \]
and finally, using \( v_x(0) = v_0 \), the full solution is
\[ \begin{aligned} v_x(t) = v_0 e^{-t/\tau}, \end{aligned} \]
introducing the quantity \( \tau \equiv m/b \), sometimes called the "natural time" or "decay time". So, the speed as a function of time will decay to zero exponentially like so:

Although we ignored the actual position \( x \) to get here, now that we have the solution, it's easy to reconstruct:
\[ \begin{aligned} x(t) = x(0) + \int_0^{t} dt' v_x(t') = x_0 + v_0 \int_0^t dt' e^{-t'/\tau} \\ = x_0 -\tau v_0 \left. e^{-t'/\tau} \right|_0^{t} \\ = x_0 + \tau v_0 (1 - e^{-t/\tau}). \end{aligned} \]
As \( t \) goes to infinity, the distance traveled by the cart approaches \( \Delta x_\infty = \tau v_0 \):
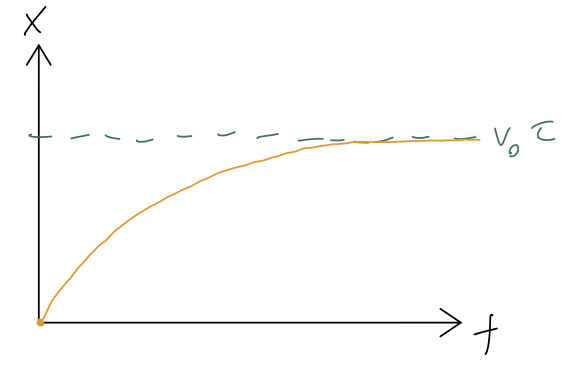
Notice that the natural time \( \tau \) popped up again: the total distance traveled by the cart when it stops is exactly the same as the distance it would have traveled with no drag in time \( \tau \). This isn't a deep statement: it's more of an example of dimensional analysis, which is the idea that we can often guess the right answer (or close to it) just by putting together known quantities in the only way that their units will allow. In this case, given \( v_0 \) and \( \tau \), the only thing we can build with units of distance is \( v_0 \tau \).
Linear drag and freefall
Now that we're warmed up, let's move on to the more interesting case of an object in freefall. We can restrict ourself to a single coordinate \( y \), and draw the free-body diagram:
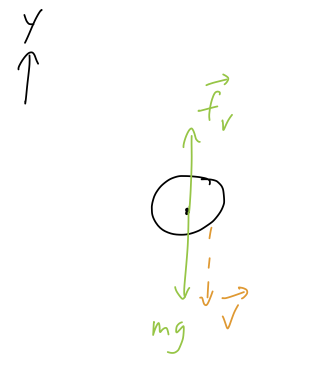
This diagram assumes that velocity is pointing down in this instant. To avoid confusion, we need to be very, very careful about minus signs and what direction things are pointing in!
Clicker Question
Which is the correct equation of motion, given the free-body diagram above (with \( y \) pointing up)?
A. \( m \dot{v}_y = mg - bv_y \)
B. \( m \dot{v}_y = -mg - bv_y \)
C. \( m \dot{v}_y = mg + bv_y \)
D. \( m \dot{v}_y = -mg + bv_y \)
Answer: B
It's best to start with the direction of gravity, which is easier to think about. Since our \( y \) direction is pointing up, the force due to gravity is pointing in the \( -\hat{y} \) direction, which means that it should have a minus sign. So the right answer must be either B or D.
The drag force, on the other hand, is pointing up - it has to be a positive contribution to \( m \dot{v}_y \). But remember that the diagram assumes \( v_y \) itself is pointing down, which means that it is negative! So \( -bv_y \) is positive, giving us answer B.
Clicker Question
Now suppose the object has speed pointing up, giving the free-body diagram shown below. Which equation of motion is correct?
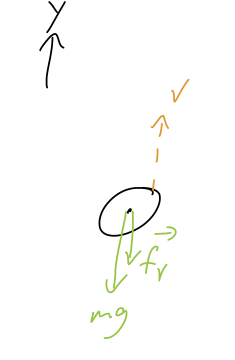
A. \( m \dot{v}_y = mg - bv_y \)
B. \( m \dot{v}_y = -mg - bv_y \)
C. \( m \dot{v}_y = mg + bv_y \)
D. \( m \dot{v}_y = -mg + bv_y \)
Answer: B
Yes, the answer is still B! The direction of drag force is reversed, but so is the sign of \( v_y \), meaning that we don't have to change anything - equation B still works correctly to give us the right directions for everything.
If you're comparing to Taylor, note that he assumes \( \vec{v} \) is pointing down and there are some minus-sign differences as a result. For us, dividing through our result above gives the first-order ODE
\[ \begin{aligned} \dot{v}_y = -g - \frac{b}{m} v_y. \end{aligned} \]
(Don't forget, \( v_y \) is positive for upwards motion, negative for downwards!) Before we move on to talk about solutions, we can already notice something interesting just from the equation of motion itself. There is a particular speed for which the right-hand side of the equation will vanish:
\[ \begin{aligned} v_{y} = -v_{\rm ter} = -\frac{mg}{b}. \end{aligned} \]
For an object free-falling at this speed, the drag force balances gravity and there is no acceleration. This speed is known as the terminal velocity, because it is the maximum possible speed that can be reached for an object dropped from rest. (Note that I took out a minus sign, so that the terminal velocity will always be a positive number, matching Taylor's definition.)
In fact, this is the final speed that will be reached for any initial speed, even if we launch an object faster than \( v_{\rm ter} \)! For \( vy < -v{\rm ter} \), the equation of motion tells us that \( \dot{v}y > 0 \), so the object will decelerate until it reaches \( v{\rm ter} \) and the forces balance.
Now let's find a solution. There is more than one way to do this: Taylor shows you one way involving a \( u \)-substitution. I'll use the method of particular solutions instead. First, we should notice that this equation is inhomogeneous, because of the \( g \). The complementary equation is
\[ \begin{aligned} \dot{v}_{y,c} + \frac{b}{m} v_{y,c} = 0. \end{aligned} \]
We just solved this for horizontal motion; we know the answer is
\[ \begin{aligned} v_{y,c}(t) = Ce^{-bt/m}. \end{aligned} \]
Next, we need a particular solution. As before, because the inhomogeneous piece is just a constant, a constant particular solution will work: if we write
\[ \begin{aligned} v_{y,p}(t) = -\frac{mg}{b} = -v_{\rm ter}, \end{aligned} \]
then \( \dot{v}_{y,p} = 0 \) and the full equation is satisfied. Our general solution just requires putting them together:
\[ \begin{aligned} v_y(t) = v_{y,c}(t) + v_{y,p}(t) = -v_{\rm ter} + Ce^{-bt/m}. \end{aligned} \]
Finally, we apply our initial condition to fix the constant \( C \):
\[ \begin{aligned} v_y(0) = v_0 = -v_{\rm ter} + C \\ \Rightarrow C = v_0 + v_{\rm ter} \end{aligned} \]
or plugging back in, and putting in the natural time \( \tau = m/b \) like we did before,
\[ \begin{aligned} v_y(t) = v_0 e^{-t/\tau} - v_{\rm ter} (1 - e^{-t/\tau}). \end{aligned} \]
If \( v_0 = 0 \), this looks exactly like what the \( x \)-dependence looked like for the horizontal case: the speed starts at zero and grows like an inverse exponential, asymptoting towards the (negative) terminal velocity. More generally, the dependence on the initial speed \( v_0 \) will decay exponentially, so that as we discussed any solution will approach the terminal velocity at large enough times.