Last time, we were trying to prove conservation of linear momentum for a collection of \( N \) particles. We ended on the equation:
\[ \begin{aligned} \frac{d\vec{P}}{dt} = \sum_\beta \frac{d\vec{p}_\beta}{dt} = \sum_\beta \vec{F}_\beta \\ = \sum_\beta \left( \sum_{\alpha \neq \beta} \vec{F}_{\beta \alpha} + \vec{F}_{\beta, \rm{ext}} \right). \end{aligned} \]
Before we continue the derivation, a quick clicker question to make sure we understand what the sum means.
Clicker Question
How many terms are in the 'sum of sums' over all internal forces?
\[ \begin{aligned} \sum_\beta \sum_{\alpha \neq \beta} \vec{F}_{\beta \alpha} \end{aligned} \]
A. \( N^2 \)
B. \( N^2 - 1 \)
C. \( N^2 - N \)
D. \( \frac{N(N-1)}{2} \)
E. \( \frac{N(N+1)}{2} \)
Answer: C
If \( \alpha \) and \( \beta \) were totally arbitrary, then there would be \( N^2 \) possible terms \( F_{\alpha \beta} \), since each index separately goes from \( 1 \) to \( N \). However, we have to also account for the restriction \( \alpha \neq \beta \). For every value of \( \alpha \), this removes a single term from the sum. Since there are \( N \) different values of \( \alpha \) from the outer sum, the total number of terms removed is \( N \), hence answer C.
If this isn't clear yet, it may help to compare to the 2-mass case from above, or look at how I explicitly write out the sum a bit below.
Let's continue to focus on the first "sum of sums", the sum over all internal forces; in line with our 2-mass example, we expect this to add up to zero due to Newton's third law. To see any cancellation happening, we'll have to split this apart into pieces somehow. We can accomplish that by splitting apart the \( \neq \) sign:
\[ \begin{aligned} \sum_\beta \sum_{\alpha \neq \beta} \vec{F}_{\beta \alpha} = \sum_\beta \sum_{\alpha < \beta} \vec{F}_{\beta \alpha} + \sum_\beta \sum_{\alpha > \beta} \vec{F}_{\beta \alpha} \end{aligned} \]
Now, we do the following trick on the second sum: since the labels \( \alpha \) and \( \beta \) are arbitrary (like variables of integration), we can swap them. Then we notice that because the double sum means "sum over all pairs \( (\alpha, \beta) \) where \( \beta > \alpha \)", we can invert the order of the sums and rewrite the inequality:
\[ \begin{aligned} \sum_\beta \sum_{\alpha > \beta} \vec{F}_{\beta \alpha} = \sum_\alpha \sum_{\beta > \alpha} \vec{F}_{\alpha \beta} = \sum_{\beta} \sum_{\alpha < \beta} \vec{F}_{\alpha \beta} \end{aligned} \]
Putting things back together gives
\[ \begin{aligned} \sum_\beta \sum_{\alpha \neq \beta} \vec{F}_{\beta \alpha} = \sum_\beta \sum_{\alpha < \beta} (\vec{F}_{\beta \alpha} + \vec{F}_{\alpha \beta}) \end{aligned} \]
and finally using the third law, \( \vec{F}{\alpha \beta} = -\vec{F}{\beta \alpha} \), so this sum just vanishes! Thus, we have the result we wanted,
\[ \begin{aligned} \frac{d\vec{P}}{dt} = \vec{F}_{\rm{net, ext}}. \end{aligned} \]
Part of the reason we're doing this exercise with sums is so that you can get a little bit of experience in this kind of sum manipulation where we switch indices around. In case those index-manipulation steps went too fast for you, and in general for sum problems like this, it can be a good idea to write things out more explicitly. Here's what the terms in the sum look like without summation notation, excluding the \( \vec{F}_{\rm ext} \) pieces:
\[ \begin{aligned} \vec{F}_{1,{\rm int}} = 0 + \vec{F}_{12} + \vec{F}_{13} + ... + \vec{F}_{1N} \\ \vec{F}_{2,{\rm int}} = \vec{F}_{21} + 0 + \vec{F}_{23} + ... + \vec{F}_{2N} \\ \vec{F}_{3,{\rm int}} = \vec{F}_{31} + \vec{F}_{32} + 0 + ... + \vec{F}_{3N} \\ ... \end{aligned} \]
I've explicitly written zeroes in place of the ''missing'' diagonal terms \( \vec{F}{11}, \vec{F}{22}... \) to make the pattern more obvious. For the few terms we've written out, we see the third-law cancellation: every \( \vec{F}{\alpha \beta} \) has a corresponding \( \vec{F}{\beta \alpha} \) on the opposite side of the diagonal.
We can also now see what the arcane sum manipulations I did above mean more explicitly. When we divide up the sum over \( \alpha \neq \beta \), the \( \alpha < \beta \) piece of \( \vec{F}_{\beta \alpha} \) is all the terms below the diagonal, while \( \alpha > \beta \) is the terms above. But saying "all possible \( \vec{F}_{\alpha \beta} \) where \( \alpha < \beta \)" is clearly also all the terms above the diagonal.
So we've shown that the total momentum of any collection of physical objects changes only according to the net external force. This is a very powerful result! In particular, momentum conservation will let us make detailed statements about mechanics problems without knowing anything about the (often very complicated!) internal forces at work. Here are a few nice examples, briefly:
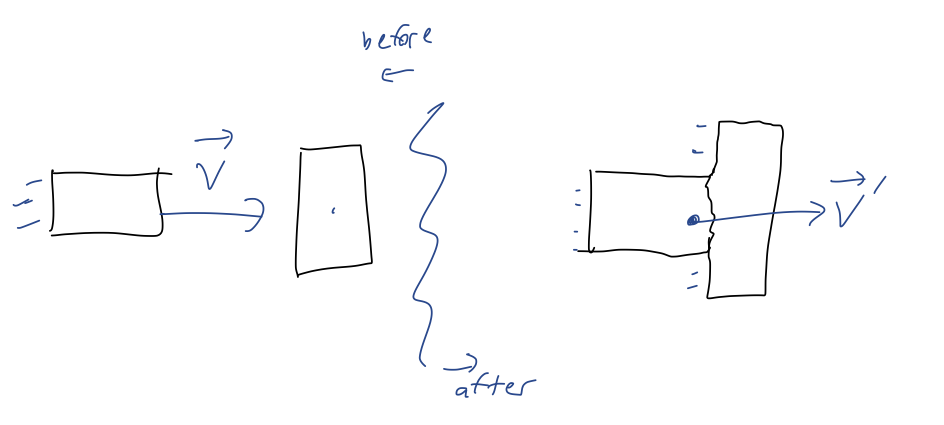
- Inelastic collisions: for example, a car crash certainly involves a lot of complicated internal forces. But knowing how the crashed cars moved together after the collision, e.g. from looking at marks left on the road, can give enough information to investigators to reconstruct what happened before the collision. Another example could be one football player tackling another one; we can relate the initial speed of both players to the speed after the tackle, which might be important if you're studying sports medicine for example.
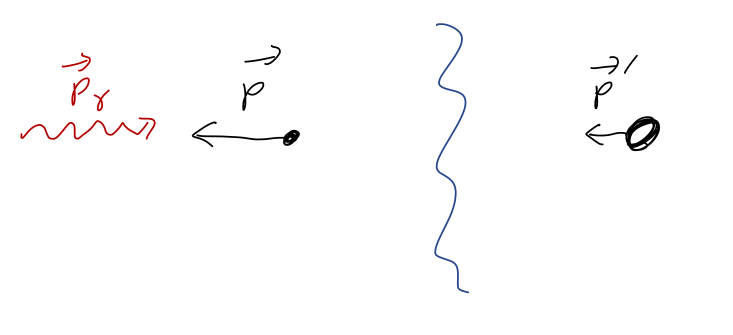
- Laser cooling and laser sails: you'll recall from modern physics that photons carry momentum, \( p = h/\lambda \). Although we've only proved it for Newtonian mechanics, momentum conservation actually holds down to the most fundamental theories we know of! So we can understand the idea of laser cooling: if we shine a laser on an atom at the right frequency, the atom can absorb the photon. When it does, momentum conservation tells us that the atom has to slow down. At a larger scale, a laser sail works by shining a laser at a highly reflective surface. The photons bounce off in the opposite direciton, pushing the sail forward according to momentum conservation. This is a promising method of propulsion for very small spacecraft.
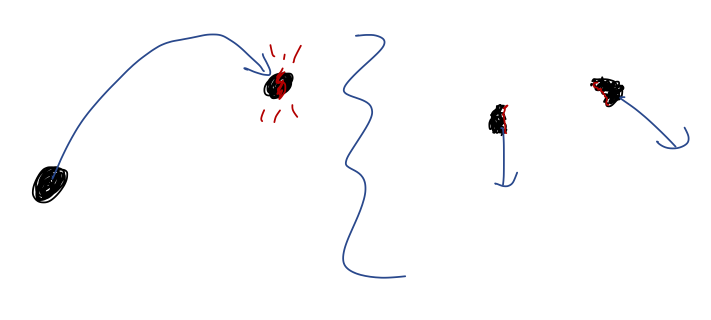
- Explosions: something like a firework detonation, or a rocket separating off one of its stages. Again, the internal forces involved here can be complicated and violent, but nevertheless momentum conservation constrains the combined motion of all the pieces. If we track N-1 pieces after the explosion, we know exactly the trajectory of the last piece.
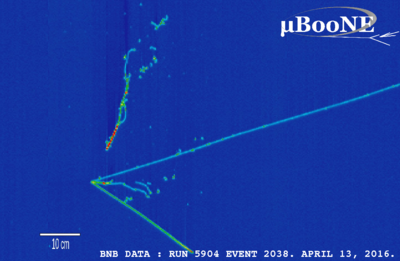
- Invisible particles: this is really just another explosion example, but it's an interesting one! The study of subatomic particles makes heavy use of momentum conservation. The picture above, from the MicroBooNE experiment at Fermilab, shows visible tracks for charged particles passing through their detector. However, notice that all of the tracks point back to a single point, and if we try to add up the total momentum it's definitely pointing to the right. We can thus infer that there was an incoming particle that is invisible to our detector, which collided at the vertex where the tracks meet and caused the visible particles to fly off. (In fact, this invisible particle is a neutrino, and is precisely the particle that the MicroBooNE experiment was designed to look for.) This is cutting-edge research, but we don't need to know any details of particle physics to understand the basic idea, just momentum conservation!
Example: breaking up
A hockey puck is traveling in the \( +\hat{x} \) direction at constant speed \( v_0 \) m/s. Suddenly, it breaks apart into two pieces which travel off at \(\theta_1 = 60^\circ\) and \(\theta_2 = 30^\circ\) as pictured:
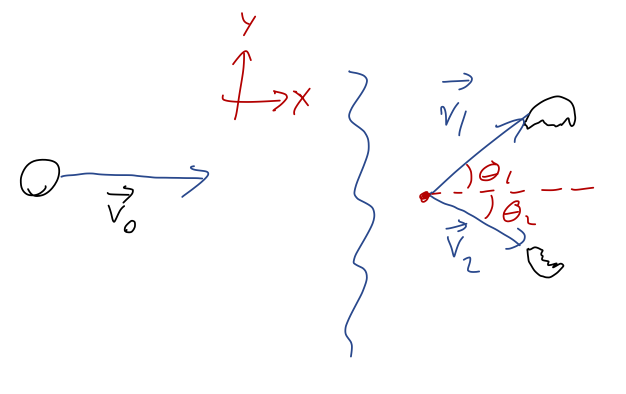
If the first piece is moving at \( v_1 = 4 \) m/s, and its mass is equal to \( 2/3 \) of the total mass of the hockey puck, what is the speed \( v_2 \) of the other piece?
Since there are no external forces, we have conservation of total momentum \( \vec{P} \), which is most usefully written as \(\vec{P}_{\rm initial} = \vec{P}_{\rm final}\). This gives us two conservation equations, one for the \( \hat{x} \) components and one for the \( \hat{y} \) components:
\[ \begin{aligned} (m_1 + m_2) v_0 = m_1 v_1 \cos \theta_1 + m_2 v_2 \cos \theta_2 \\ 0 = m_1 v_1 \sin \theta_1 - m_2 v_2 \sin \theta_2 \end{aligned} \]
To relate \( v_2 \) to \( v_1 \), we can just use the second equation for the vertical components. Doing some algebra,
\[ \begin{aligned} m_1 v_1 \sin \theta_1 = m_2 v_2 \sin \theta_2 \\ v_2 = \frac{m_1 \sin \theta_1}{m_2 \sin \theta_2} v_1 \end{aligned} \]
If the total mass of the hockey puck is \( M \), then since \( m_1 = 2M/3 \), we know that \( m_2 = M/3 \), since they have to add up to \( M \). So \( m_1 / m_2 = 2 \). Plugging in \( \sin \theta_1 = \sqrt{3}/2 \) and \( \sin \theta_2 = 1/2 \), we end up with
\[ \begin{aligned} v_2 = 2 \sqrt{3} v_1 = 8 \sqrt{3}\ {\rm m} / {\rm s}, \end{aligned} \]
or about 13.8 m/s.
We only had to use conservation of momentum in the \( \hat{y} \) direction to get this far, so we still have the other equation involving \( P_x \). We could continue and use that equation to find the only unknown quantity left, which is the speed \( v_0 \). But this won't really be any different from the calculation we just did, so I'll stop here.
Now let's try another example, along the lines of the 'invisible particles' example from before.
Clicker Question
A lithium-8 nucleus decays in the following way:
\[ \begin{aligned} {}^8{\rm Li} \rightarrow {}^8{\rm Be} + e^{-} + \bar{\nu} \end{aligned} \]
Suppose the lithium-8 nucleus begins at rest, and the \( ^8{\rm Be} \) nucleus and the electron are measured to be moving with momenta as shown in the diagram below. What is the momentum \( p_\nu \) of the neutrino, in the form \( (p_x, p_y) \)? (Use the fact that \( \cos 45^\circ = \sin 45^\circ \approx 0.7 \). All momenta are given in units of \( MeV/c \).)
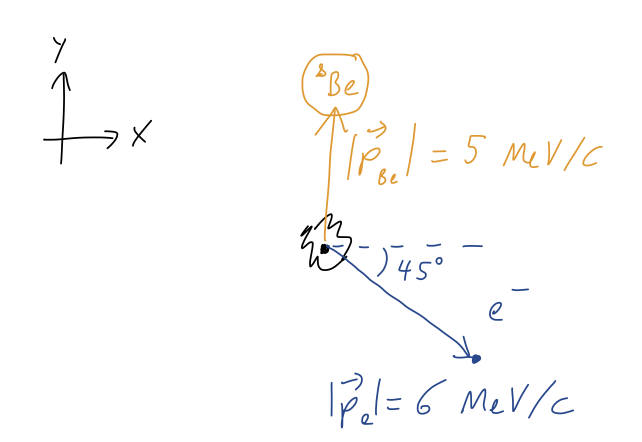
A. (4.2, 4.2)
B. (-5, 0)
C. (-5, -1)
D. (-4.2, 0.8)
E. (-4.2, -0.8)
Answer: E
Momentum conservation tells us that \( \vec{P}{\rm initial} = \vec{P}{\rm final} \); since the initial decaying nucleus begins at rest, we know that
\[ \begin{aligned} \vec{P}_{\rm initial} = (0,0). \end{aligned} \]
So the momentum of all three final products has to also add up to zero in both directions. Let's begin by finding the momentum components of the two visible products. For the beryllium nucleus, we can simply read off the figure that
\[ \begin{aligned} \vec{p}_{\rm Be} = (0, 5). \end{aligned} \]
For the electron, we see that the components are
\[ \begin{aligned} \vec{p}_{\rm e} = (6 \cos 45^\circ, -6 \sin 45^\circ) = (4.2, -4.2). \end{aligned} \]
Adding together, we find a total momentum of \( \vec{p}{\rm Be + e} = (4.2, 0.8) \). Since the total for all three particles has to be zero, we see that \( p{\nu} = (-4.2, -0.8) \), matching option E.
Example: momentum conservation
I'm standing on a boat in a completely still lake, near a dock. Everything starts at rest. If I walk at constant speed on the boat, in the direction away from the dock, how does the distance between me and the dock change?
There's a few things to keep track of here: the boat, the dock, and me. Step one is to sketch some coordinates, then:
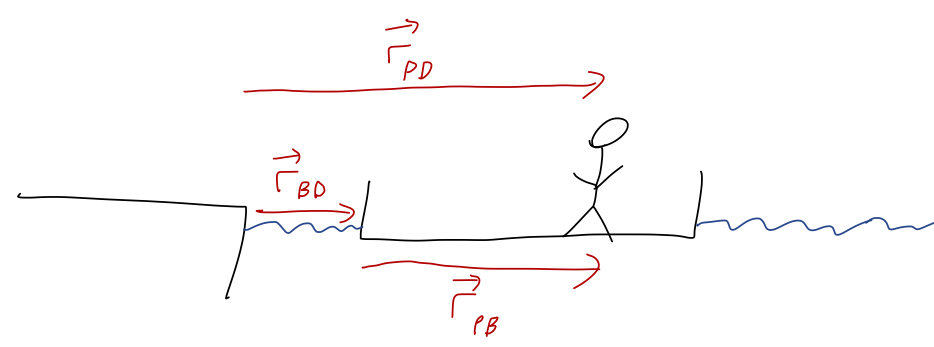
using subscripts for relative position, i.e. \( \vec{r}_{PD} \) is position of the person, relative to the dock. With the coordinate labels as given above, it's clear that there is a relationship between them, namely
\[ \begin{aligned} \vec{r}_{BD} + \vec{r}_{PB} = \vec{r}_{PD}. \end{aligned} \]
Taking time derivatives, the same relation holds for speeds,
\[ \begin{aligned} \vec{v}_{BD} + \vec{v}_{PB} = \vec{v}_{PD}. \end{aligned} \]
Momentum is a different story, because for momentum the mass of each object matters. Since the dock position is fixed, the two momenta we have to keep track of are
\[ \begin{aligned} \vec{p}_{BD} = m_B \vec{v}_{BD} \\ \vec{p}_{PD} = m_P \vec{v}_{PD} \end{aligned} \]
and then \(\vec{P} = \vec{p}_{BD} + \vec{p}_{PD}\) for the total momentum. (Note that we don't need to try to include the person-boat relative motion when defining \( \vec{P} \); we've included all of the moving objects just with these two momentum vectors.)
Given that everything starts at rest, we know that \( \vec{P} = 0 \) at \( t=0 \). Since there are no external forces, momentum conservation thus tells us that \( \vec{P} \) is always zero. This gives us the relation
\[ \begin{aligned} \vec{P} = 0 = m_B \vec{v}_{BD} + m_P \vec{v}_{PD} \\ = m_B \vec{v}_{BD} + m_P (\vec{v}_{BD} + \vec{v}_{PB}) \\ \Rightarrow \vec{v}_{BD} = -\frac{m_P}{m_P + m_B} \vec{v}_{PB}. \end{aligned} \]
In other words, if the person starts walking at speed \( \vec{v}_0 \), the boat moves relative to the dock with speed given in this formula. The minus sign indicates that as we walk away from the dock, the boat moves towards it. We can also plug this in to the relation between the three velocities to find the person's motion relative to the dock:
\[ \begin{aligned} \vec{v}_{PD} = \vec{v}_{BD} + \vec{v}_{PB} = +\frac{m_B}{m_P + m_B} \vec{v}_{PB}. \end{aligned} \]
It's useful to consider the limits of \( m_B \) here. If the boat is very light, say \( m_B \sim m_P \), then it's very easy for our motion to influence the boat's motion; our walking will push the boat towards the dock, and as a result we won't move as quickly away from the dock as we would on dry land. On the other hand, if \( m_B \gg mP \), then \( \vec{v}{BD} \) approaches zero while \(\vec{v}_{PD} \rightarrow \vec{v}_{PB}\). (In other words, for a heavy enough boat, our effect on the boat's motion is imperceptible and it's as if we're just walking on land.)
Just for fun, let's plug in some numbers on a larger-scale example. The largest cruise ship in the world is the Royal Caribbean Symphony of the Seas, with a mass of about 100,000 tons, or \( 9 \times 10^7 \) kg. At maximum capacity, the Symphony can hold 7,718 people. Assuming an average person weighs about 60 kg, what would happen if everyone lined up at one end of the ship and ran to the other end at \( v = 5 \) m/s?
Treating all the people as one mass \( mP = 7718 \times (60\ {\rm kg}) = 4.6 \times 10^5 \) kg moving together, then \( v{PB} \) is 5 m/s, and we can plug in to our formula assuming \( \vec{v}_{BD} = 0 \), i.e. the boat is initially at rest:
\[ \begin{aligned} \vec{v}_{BD} = -\frac{4.6 \times 10^5\ {\rm kg}}{4.6 \times 10^5\ {\rm kg} + 9 \times 10^7\ {\rm kg}} (+5\ {\rm m}/{\rm s}) = 0.025\ {\rm m}/{\rm s} \end{aligned} \]
or 0.06 mph. So I don't think anything noticeable will happen to the ship - it's simply too heavy! (On the other hand, if you've been on a small few-person boat on a lake, you know that your own movements can have a significant effect on how the boat moves.)