External forces and center of mass
Before we move on to apply things, we need to study the effect of external forces a little more. In the presence of an external force, total momentum is not conserved, since
\[ \begin{aligned} \frac{d\vec{P}}{dt} = \vec{F}_{\rm net, ext}. \end{aligned} \]
However, we will find that the way in which the momentum changes due to \( \vec{F}_{\rm net, ext} \) is simple and predictable. So even for problems where external forces are present (and most realistic problems have gravity at least!), we'll be able to split the problem up into the motion due to external force, and then applying momentum conservation for the rest.
Going back to our system of \( N \) point masses, let's now think about their positions \( \vec{r}_1, ..., \vec{r}_N \). Since the momentum of a point mass is
\[ \begin{aligned} \vec{p}_\alpha = m_\alpha \dot{\vec{r}}_\alpha, \end{aligned} \]
we can actually rewrite the total momentum in terms of individual speeds,
\[ \begin{aligned} \vec{P} = \sum_\alpha \vec{p}_\alpha = \sum_\alpha m_\alpha \dot{\vec{r}}_\beta. \end{aligned} \]
Just based on dimensions, if we divide \( \vec{P} \) by a mass scale, we'll get a velocity vector of some sort. Since this is the total momentum, it makes the most sense to divide by the total mass: if
\[ \begin{aligned} M = \sum_\beta m_\beta \end{aligned} \]
then we define the total velocity vector to be
\[ \begin{aligned} \vec{V} = \frac{\vec{P}}{M} = \frac{1}{M} \sum_{\alpha=1}^N m_\alpha \dot{\vec{r}}_\alpha. \end{aligned} \]
Looking at the definition, this is just the time derivative of another vector, which we'll call the center of mass (or "CM") position vector:
\[ \begin{aligned} \vec{V} = \dot{\vec{R}},\ \ \vec{R} = \frac{1}{M} \sum_{\alpha=1}^N m_\alpha \vec{r}_\alpha. \end{aligned} \]
Some references will write this as \(\vec{R}_{CM}\) to be explicit; I'll skip the subscript as long as it's clear from context. The CM vector \( \vec{R} \) gives sort of a weighted average of the positions of all the objects in our system, with weighting proportional to their mass. And now we notice that if we go back to the equation for external net force, we find
\[ \begin{aligned} \frac{d\vec{P}}{dt} = M \ddot{\vec{R}} = \vec{F}_{\rm net, ext}. \end{aligned} \]
So the center of mass position evolves like a point particle with total mass \( M \), following Newton's second law and subject to the net external force acting on the system. This immediately justifies a common approximation used in mechanics, which is that we can treat large, extended objects the same way we treat point particles when applying Newton's laws.
Of course, most everyday objects are pretty complicated, and in fact even a tennis ball is made of an incredible large number of individual tennis-ball particles. For situations where \( N \) would be very large, we can instead replace the sum with an integral. (Think back to your calculus class - this is how integrals are originally defined!)
For the situation where \( N \) is very large, we can replace the discrete set of point masses \( { m_\alpha } \) with a continuous set of infinitesmal masses \( dm \). (Notation aside: curly brackets is math notation for a set, which is a collection of mathematical objects. \( m_\alpha \) denotes one point mass; \( { m_\alpha } \) is the collection of all of them.) Since each tiny speck of mass has its own position, we have to define a function of position \( \vec{r} \) to keep track of them. We define the mass density function \( \rho(\vec{r}) \) through the relationship
\[ \begin{aligned} dm = \rho(\vec{r})\ dV \end{aligned} \]
By inspection \( \rho(r) \) has units of mass per unit volume, \( [M]/[L]^3 \). With this definition, all of the sums over masses become integrals over \( dm \):
\[ \begin{aligned} M = \int dm = \int \rho(\vec{r}) dV \\ \vec{R} = \frac{1}{M} \int \vec{r}\ dm = \frac{1}{M} \int \rho(\vec{r}) \vec{r}\ dV. \end{aligned} \]
and we could write similar formulas for \( \vec{P} \) and \( \vec{V} \), but they're easily obtained by just taking derivatives of \( \vec{R} \).
Don't get confused by the fact that we're integrating over a vector! Since both sides of the equation are vectors, this is really just three separate integrals for each of the components, i.e. in Cartesian components
\[ \begin{aligned} X_{CM} = \frac{1}{M} \int x\ dm,\ \ Y_{CM} = \frac{1}{M} \int y\ dm,\ \ Z_{CM} = \frac{1}{M} \int z\ dm. \end{aligned} \]
The components are almost always found in Cartesian components, even if the integrals themselves are easier to do in cylindrical, spherical, etc. coordinates.
Clicker Question
A long, rigid rod of mass \( m \) is floating in space. If you push (momentarily!) on the bottom end of the rod, what does it do in response?
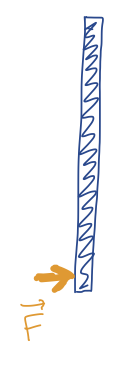
A. Rotates in place, but the CM doesn't move.
B. Accelerates to the right, with \( a_{\rm CM} < F / m \).
C. Accelerated to the right, with \( a_{\rm CM} = F / m \).
D. Something else, or we don't have enough information to say.
Answer: C
This is an interesting puzzle, but ultimately we can rely on a very simple concept: we just showed that any extended object will behave like a point particle in terms of obeying Newton's second law. The second law tells us the answer has to be C!
Of course, there will be some rotational motion as well - you can try this out by flicking a pen or pencil on a flat surface. But you'll notice immediately that there is still forward motion in addition to the rotation, and that forward motion is exactly given by \( \vec{F} = m\vec{a} \).
Your intuition may strongly lead you to answer B, instead of C. The typical argument goes: since the object is both rotating and accelerating to the right, some of the force must be "used up" to cause the rotation, so \( a_{\rm CM} \) will be smaller than \( F/m \). The problem with this argument is that it's secretly an argument about energy - force can't be "used up" or divided, so the same force provides both the linear acceleration and the torque for the rotation.
In terms of energy, we haven't talked about it yet in detail, but I'll give the short version of the story here. Imagine applying the same force to the center of the rod, right at the CM. This will give exactly the same linear acceleration of \( F/m \), but it won't give any rotation. If we apply both forces for the same amount of time \( \Delta t \), the final momentum (and thus speed) will be the same no matter where we push the rod. Therefore, the kinetic energy \( \frac{1}{2} mv^2 \) will be the same. But in the rotating case, there is an additional rotational energy term - so where does the extra energy come from?
The answer is that change in energy is not just given by force, but force times distance (which is the definition of work, \( W \).) In the case where the force is applied at the bottom of the rod, if \( \Delta t \) is kept fixed, we will apply the same force over a longer distance as the bottom of the rod spins away from us. This is where the extra energy for the rotational motion comes from.
Finding the center of mass
Before we get into doing integrals, it's a good idea to run through the center of mass calculation for two point masses, which we'll call \( m_1 \) and \( m_2 \). Let's set up our coordinates like this:
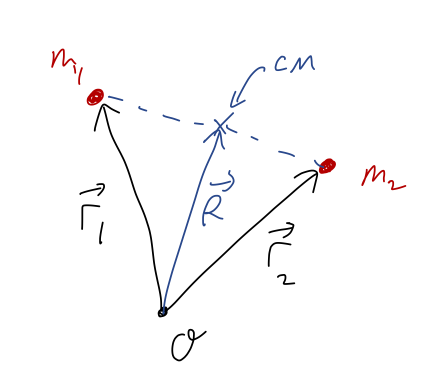
Using our formulas above, we have
\[ \begin{aligned} \vec{R} = \frac{m_1}{m_1 + m_2} \vec{r}_1 + \frac{m_2}{m_1 + m_2} \vec{r}_2 \end{aligned} \]
Notice that if we take \( m_1 \rightarrow 0 \), then the CM position approaches \(\vec{R} = \vec{r}_2\), and vice-versa. So the CM position tends to be closest to the heavier mass. On the other hand, if \(m_1 = m_2\), then
\[ \begin{aligned} \vec{R} = \frac{1}{2}(\vec{r}_1 + \vec{r}_2) \end{aligned} \]
which is exactly in the center between the masses.
We can make a couple more nice observations in the two-mass case by changing coordinates. First, let's try setting \( \vec{r}_1 = 0 \), i.e. putting mass 1 at the origin of our coordinates. Then we have
\[ \begin{aligned} \vec{R} \rightarrow \frac{m_2}{m_1 + m_2} \vec{r}_2 \end{aligned} \]
so \( \vec{R} \) points in the same direction as \( \vec{r}_2 \). In other words, the position of the center of mass is along the line between \( m_1 \) and \( m_2 \).
Finally, let's put our coordinate origin at the geometric center, exactly halfway in between \( \vec{r}_1 \) and \( \vec{r}_2 \) as shown:
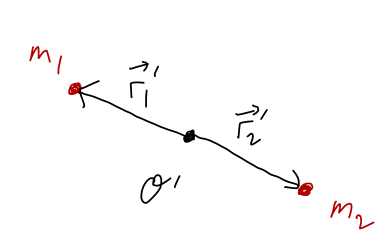
Measured from this point, we have \( \vec{r}'_2 = -\vec{r}'_1 \). Using this relation in the general formula gives
\[ \begin{aligned} \vec{R} = \frac{m_1}{m_1 + m_2} \vec{r}'_1 - \frac{m_2}{m_1 + m_2} \vec{r}'_1 \end{aligned} \]
In general, the CM is not at the geometric center; it will be closer to the heavier mass out of \( m_1 \) or \( m_2 \). However, in the special case where \( m_1 = m_2 \), the two terms are equal and opposite and cancel completely. The situation where this cancellation happens is said to exhibit reflection symmetry or mirror symmetry about the origin; mirror reflection takes \( \vec{r} \rightarrow -\vec{r} \), so with \( \vec{r}'_2 = -\vec{r}'_1 \) we can think of mass 2 as a 'reflection' of mass 1 if they are identical.