Continuing from last time, we were talking about reflection symmetry and when the center of mass is zero. The case of two masses probably seems like a really special case, but notice what happens if we add two more masses along a different line:
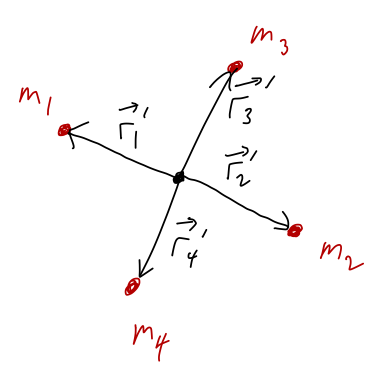
With \( \vec{r}'_4 = -\vec{r}'_3 \), we have
\[ \begin{aligned} \vec{R} = \frac{m_1 - m_2}{M} \vec{r}'_1 + \frac{m_3 - m_4}{M} \vec{r}'_3 \end{aligned} \]
and once again, if the pairs \((m_1, m_2)\) and \((m_3, m_4)\) are reflection symmetric, then both pairs contribute zero to the CM position and we find \( \vec{R} = 0 \).
What we're seeing is a very general and powerful rule that applies to calculating the center of mass: if we have two equal masses \(m_1 = m_2\) at exactly opposite positions, \(\vec{r}_1 = -\vec{r}_2\), then their total contribution to the CM is zero.
Now let's move on to the continuous case. I'll start with a simple example which will be easy to make more complicated, which is a cylinder of uniform density:
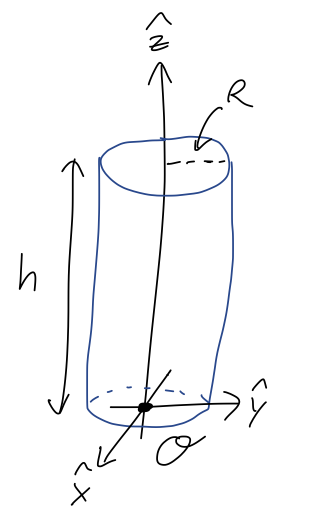
Let's just set up and do the integrals, and then we'll think about the results. With uniform (i.e. constant) density, we have simply \( \rho(\vec{r}) = \rho \). We put the origin at the center of the bottom of the cylinder, as shown. Starting with the x-position:
\[ \begin{aligned} X_{CM} = \frac{1}{M} \int x\ dm = \int x (\rho\ dV) = \frac{\rho}{M} \int_0^{2\pi} d\phi \int_0^R dr \int_0^h dz\ r x \end{aligned} \]
using cylindrical coordinates to expand out \( dV \), which gives us a factor of \( r \). (I am also using \( r \) instead of \( \rho \) for the cylindrical radius, because we have another \( \rho \) already, the density!) Thinking back to the definition of cylindrical coordinates, we recall that \( x = r \cos \phi \), so the integrand is \( r^2 \cos \phi \). All of the integrals are separate and easy to do, but let me go slowly and do them in order for this first example:
\[ \begin{aligned} X_{CM} = \frac{\rho}{M} h \int_0^{2\pi} d\phi \int_0^R dr\ r^2 \cos \phi \left.(z) \right|_0^h \\ = \frac{\rho}{M} h \int_0^{2\pi} d\phi\ \cos \phi \left. \left( \frac{1}{3} r^3 \right) \right|_0^R \\ = \frac{\rho}{3M} h R^3 \left. (\sin \phi) \right|_0^{2\pi} \\ = \frac{\rho}{3M} h R^3 (\sin 2\pi - \sin 0) = 0 \end{aligned} \]
So we just have \( X_{CM} = 0 \). I'll leave it as a short exercise to convince yourself that similarly, \( Y_{CM} \) ends up proportional to \( \cos 2\pi - \cos 0 \), so that also \( Y_{CM} = 0 \). Finally, for the \( z \) position, we have
\[ \begin{aligned} Z_{CM} = \frac{\rho}{M} \int_0^{2\pi} d\phi \int_0^R dr \int_0^h dz\ r z \\ = \frac{2\pi \rho}{M} \left(\frac{1}{2} h^2\right) \left( \frac{1}{2} R^2 \right) = \frac{\pi \rho h^2 R^2}{2M}. \end{aligned} \]
To simplify further, we recognize that \( \rho \) and \( M \) are related to each other. For constant density we just have \( M = \rho V \), but I'll just do the integral:
\[ \begin{aligned} M = \int \rho dm = \int_0^{2\pi} d\phi \int_0^R dr \int_0^h dz\ \rho r = \pi R^2 h \rho. \end{aligned} \]
Plugging back in then gives us the much simpler result
\[ \begin{aligned} Z_{CM} = \frac{h}{2}. \end{aligned} \]
Zero is a pretty special result, so let's go back and think about why we found that for \( X_{CM} \) and \( Y_{CM} \). Before we convert to cylindrical coordinates, the integral for \( X_{CM} \) can be written in the form:
\[ \begin{aligned} X_{CM} = \frac{\rho}{M} \int_{-R}^R dx\ x \int dy \int dz = \frac{\rho}{M} \int_{-R}^R dx\ x f(x) \end{aligned} \]
where \( f(x) \) is the result of doing the \( y \) and \( z \) integrals out first. We get a function of \( x \) because the \( y \) limits of integration depend on \( x \). (The function \( f(x) \) isn't too difficult to find explicitly, and if you need practice with integrating go ahead and try it!) All we need to know is that \( f(x) \) is reflection symmetric,
\[ \begin{aligned} f(-x) = f(x). \end{aligned} \]
This has to be true because if we reflect the cylinder along the \( x \)-axis about the origin, it looks completely identical. (I say "reflect along the \( x \)-axis", but really what this means is you should imagine a plane perpendicular to the x-axis and containing the origin. That plane is acting like a mirror for the reflection.)
Knowing this one geometric fact, we have
\[ \begin{aligned} X_{CM} \propto \int_{-R}^R dx\ x f(x) = \int_{-R}^0 dx\ x f(x) + \int_0^R dx\ x f(x) \\ = \int_R^0 (-dx) (-x) f(-x) + \int_0^R dx\ x f(x) \\ = -\int_0^R dx\ x f(x) + \int_0^R dx\ x f(x) = 0. \end{aligned} \]
(the symbol \( \propto \) means "is proportional to", i.e. ignoring the \( \rho/M \) out front.) Similarly, the fact that the cylinder is identical if we reflect along the \( \hat{y} \)-axis lets us predict immediately that \( Y_{CM} = 0 \), even before we actually do the integral. This doesn't work for the \( \hat{z} \) direction, because if we reflect about the origin, (i.e. through a plane containing the origin and perpendicular to \( \hat{z} \)), our sketch looks different:
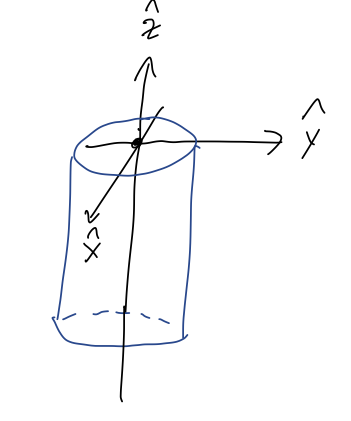
On the other hand, if we put the origin halfway up the cylinder's axis at \( z=h/2 \), then we have the reflection symmetry and would find \( Z_{CM} = 0 \) - exactly in agreement with our third result above. In math terms, this is the difference between integrating from \( 0 \) to \( h \) and from \( -h/2 \) to \( h/2 \) - we need the symmetric interval of integration for the two halves of the integral to cancel off.
There's a more physical explanation for why the mathematics works out this way; it's exactly the same cancellation that we saw before in our point-mass examples. Because of the reflection symmetry in the \( \hat{x} \) direction, for any little bit of mass \( dm \) that we identify in the cylinder, there is a corresponding (and identical) bit of mass \( dm \) on the other side of the origin. As we saw above, the contribution of these two masses to the CM location will balance and cancel off.
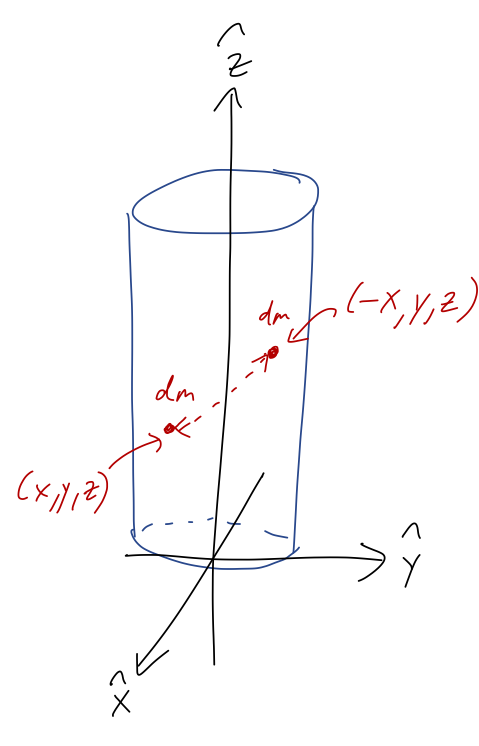
Likewise, we see that reflecting about the CM at \( Z_{CM} = h/2 \), the mass on either side in the \( \hat{z} \) direction is perfectly balanced. We could have used this observation to see that \( Z_{CM} = h/2 \), again without having to actually do any integrals. Symmetry is powerful!
Clicker Question
Consider a solid hemisphere with uniform mass density \( \rho \) and radius \( R \). Which of the pictured vectors goes through the center of mass?
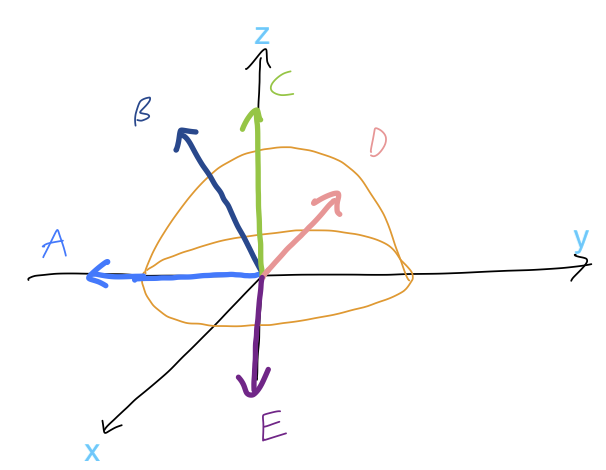
Answer: C
This is a symmetry problem! With reflection symmetry, as we've seen, we have to talk about planes of reflection, so the fact that we're now talking about lines means there must be two planes of reflection here. Indeed, since we have a hemisphere, it's easy to see that reflection along either of the axes in the plane is symmetric - in other words, \( X_{CM} = Y_{CM} = 0 \). So the only possible location for the center of mass is along the \( z \)-axis.
Since this is a hemisphere and all the mass is at positive \( z \), we must have C and not E, which is outside of the object. The CM is almost never outside of the object (unless the object is curved and/or hollow.)
Clicker Question
Continuing with the same solid hemisphere, where along the \( z \)-axis is the center of mass located? Below \( R \) is the radius of the hemisphere.
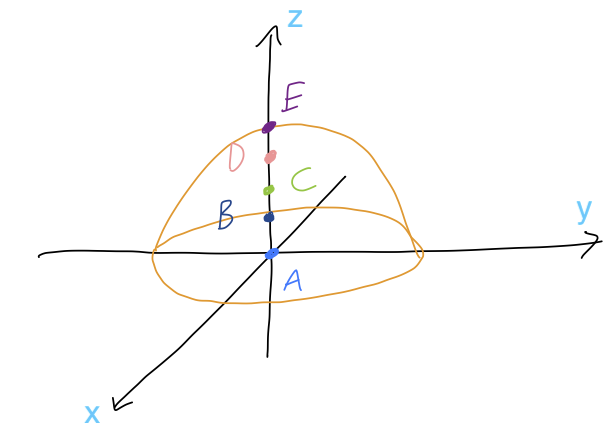
A. \( z = 0 \)
B. \( 0 < z < R/2 \)
C. \( z = R/2 \)
D. \( R/2 < z < R \)
E. \( z = R \)
Answer: B
This question requires a bit more thought, since we can't use symmetry arguments in the \( z \)-direction. It's easy to rule out the extreme cases of \( A \) and \( E \); there's no way for the CM to be at those locations, since it's an average over the \( z \)-position of all of the other infinitesmal mass points \( dm \) within the hemisphere.
To clarify this, it's helpful to go back to the formula for \( Z_{CM} \):
\[ \begin{aligned} Z_{CM} = \frac{1}{M} \int z\ dm \end{aligned} \]
Although we're not going to do the integral, we can use \( dm = \rho dV \) and think of splitting out the \( z \) part of the integration:
\[ \begin{aligned} Z_{CM} = \frac{1}{M} \int dz\ z \left( \int \rho\ dx dy \right) = \frac{1}{M} \int dz\ z M_{\circ}(z) \end{aligned} \]
The integral over \( \rho dx dy \) is just the mass of a thin slice of the hemisphere at fixed \( z \), which I wrote as \( M_\circ(z) \). So we can understand that we're just solving a one-dimensional problem over the masses of circles along the \( z \) direction. Since the circle mass is clearly decreasing as \( z \) increases, the circles at small \( z \) are heavier than the ones at large \( z \). So we expect the CM position to be skewed towards the bottom of the hemisphere: the answer must be B.
Example: find the CM
Now suppose we have a half-cylinder, cut in half through the circular direction as shown:
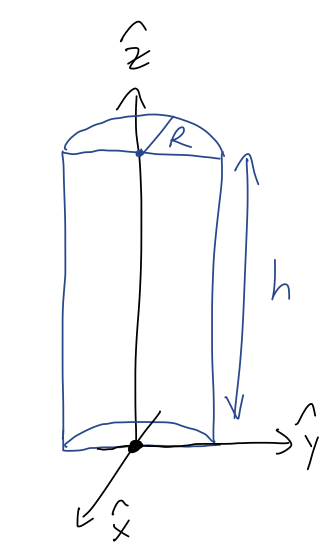
What is the CM position?
Let's begin with \( Y_{CM} \) and \( Z_{CM} \); for these two directions, we can use symmetry to find the answer without doing any math! In the \( \hat{y} \) direction, we notice that we have reflection symmetry about the axis through the middle of the half-cylinder: every point \( (x,y,z) \) in the cylinder has a matching point at \( (x,-y,z) \). So \( Y_{CM} = 0 \) by symmetry.
Similarly, in the \( \hat{z} \) direction we still have reflection symmetry about the plane halfway through the half-cylinder, so \( Z_{CM} = h/2 \) as in the previous case.
We can't apply these arguments to \( X_{CM} \), because there's nowhere that we can put a mirror perpendicular to \( \hat{x} \) that will reflect our object without giving a different image! So symmetry helped us twice, but we have to do one integral. Let's set it up: we have
\[ \begin{aligned} X_{CM} = \frac{1}{M} \int \rho\ x\ dV \\ = \frac{\rho}{M} \int_0^\pi d\phi \int_0^R r dr \int_0^h dz (r \cos \phi) \end{aligned} \]
where the only adjustment we need to make for the half-cylinder is that our polar angle runs from \( \pi/2 \) to \( 3\pi/2 \) (look carefully at the diagram!) Doing the integrals gives
\[ \begin{aligned} X_{CM} = \frac{\rho}{M} \left.\frac{hR^3}{3} (\sin \phi) \right|_{\pi/2}^{3\pi/2} \\ = -\frac{2hR^3\rho}{3M} \end{aligned} \]
(the minus sign puts it inside the half-cylinder according to our chosen coordinates, which makes sense.) Since this is a half-cylinder, its volume is just half of the standard volume, \( V = (1/2) \pi R^2 h \), which means
\[ \begin{aligned} M = \frac{1}{2} \pi R^2 h \rho \end{aligned} \]
allowing us to simplify the answer to
\[ \begin{aligned} X_{CM} = -\frac{4R}{3\pi}. \end{aligned} \]
which is about -0.4 times \( R \) - not quite halfway up the semicircle, which makes sense since there's more mass around \( x=0 \) than \( x=R \). (This is very similar to the example of the hemisphere we just considered.)