Now that we have a good idea of how to find the CM, we should step back for a moment and reflect on why it's useful to find the CM. Formally, the CM is a useful idea because if we only have external forces pushing a large object around, we can treat the whole thing as a point particle located at the CM. There are a few more specific implications of this fact:
Explosion and collision problems: Since the CM position obey's Newton's second law with respect to external forces,
\[ \begin{aligned} \vec{F}_{\rm ext} = m \ddot{\vec{R}}, \end{aligned} \]
we know that for processes with just internal forces, like an explosion, the CM will move as if no forces at all are acting upon it! (More realistically, we usually have at least gravity. For an object exploding in mid-air, for example, the CM of the pieces will continue to move as a simple free-falling point mass, even after the explosion!) Using the CM can give a more economical way to deal with such momentum-conservation problems.
Recall the broken hockey puck example from above:
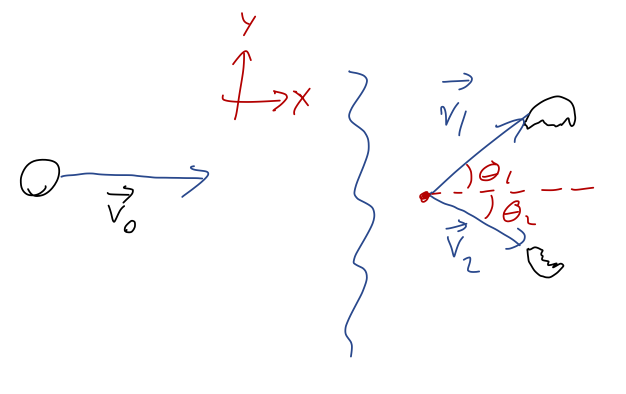
The problem we solved with momentum conservation was: given that \( v_1 = 4 \) m/s and the angles are \( \theta_1 = 60^\circ \) and \( \theta_2 = 30^\circ \), what is \( v_2 \)? We can think of this in terms of the CM instead: because there are no external forces, the CM must continue moving along the \( \hat{x} \)-axis at speed \( v_0 \) even after the puck breaks apart. Since the CM position is
\[ \begin{aligned} \vec{R} = \frac{1}{M} (m_1 \vec{r}_1 + m_2 \vec{r}_2) = \frac{2}{3} \vec{r}_1 + \frac{1}{3} \vec{r}_2, \end{aligned} \]
we can just take a time derivative of both sides to get
\[ \begin{aligned} \dot{\vec{R}} = \vec{v}_0 = \frac{2}{3} \vec{v}_1 + \frac{1}{3} \vec{v}_2 \\ (v_0, 0) = \frac{2}{3} (v_1 \cos \theta_1, v_1 \sin \theta_1) + \frac{1}{3} (v_2 \cos \theta_2, -v_2 \sin \theta_2) \end{aligned} \]
These are the same equations we found through conservation of momentum (they had to be!), but we arrived at them a bit faster. This approach of using the CM position directly for explosion and collision problems is usually an even better shortcut if the object in question breaks into more than two pieces.
Balancing forces: One of the more well-known properties of the CM is that an object can be balanced even on a point, so long that CM is directly above the balance point. We can sketch the gravity and normal forces as follows:
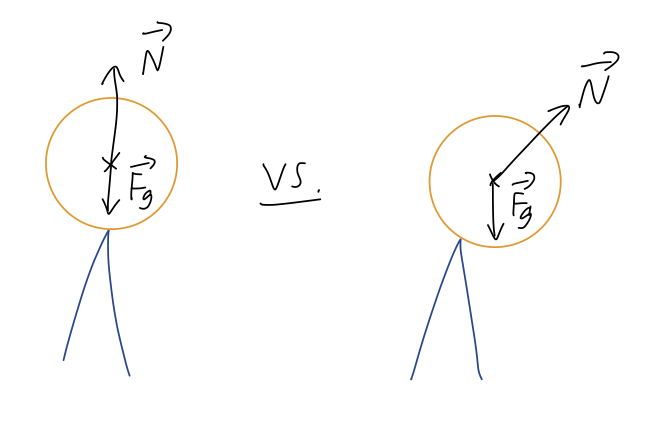
Gravity always acts straight down on the CM, but the normal force direction is always perpendicular to the contact between the surfaces. So if our object is tipped over slightly, the normal force will no longer balance against gravity completely, and the net force will cause the object to tip further.
You might ask: what if I had a completely flat object balanced on a thin rod? Once again, our flat object will tip over unless the rod is placed directly below the CM. But in this case, it seems like the normal force is always straight up, so why is the motion different?
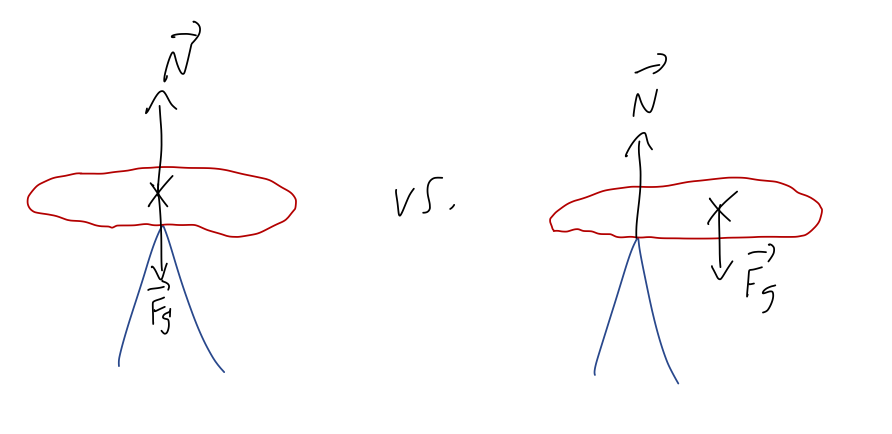
The answer is that there are two ways an extended object can move: in addition to the CM itself moving around in space, an extended object can rotate. As you'll recall from intro physics, rotation is caused by torque, \( \vec{\Gamma} = \vec{r} \times \vec{F} \). Because gravity is proportional to mass, \( \vec{F}_g \) always acts on the center of mass, but the normal force acts at the point of contact - giving a net torque and causing rotation, unless the normal force is also applied at the center of mass, in which case \( \vec{r} = 0 \) in the torque equation.
We'll consider rotation and torque, and the associated conservation law for angular momentum, at the end of this section. (Detailed study of rotation can get pretty complicated, and will mostly be left to next semester.) But first, I want to use our improved understanding of momentum conservation to tackle one more new type of problem, which is rocket propulsion.
Rockets
The basic idea of rocket propulsion follows directly from what we've seen about conservation of momentum. For a compound system, as we've seen, we can change the momentum of one part of the system by causing some motion to happen to another part. In our boat example problem, the person can actually move the entire boat just by walking across it in the opposite direction. However, there are practical limits in that case: the person can only walk so far, and as we saw the distance from person to dock always increases in that example - so you can't use this trick to make it back to dry land if your motor shuts off.
A better way to exploit conservation of momentum in the boat example is by using projectiles. If you take an object on the boat and throw it overboard, conservation of momentum requires that the boat will be pushed forward in the opposite direction. Since the object is separated from the boat, we can get closer to dry land in this way - the only practical limit is how many things we have to throw in order to propel ourselves forwards.

This is, in fact, an example of rocket propulsion: the idea of propelling a vessel forwards by ejecting part of its mass in the opposite direction that we want to travel. If we consider the vessel and the ejected mass to be part of the same system, there are only internal forces active, so we have \( d\vec{P}/dt = 0 \). Of course, throwing things by hand isn't very efficient; when I say the word "rocket", you probably picture something that uses a chemical reaction to eject super-hot gas.
Keeping the latter example in mind, we'll assume our rocket is continuously ejecting mass at a rate \( dm/dt \), so the rocket itself has a mass-dependent time \( m(t) \). The speed at which the mass is ejected, called the exhaust speed \( v_{\rm exh} \), is also important. To begin with, we'll assume all external forces are zero; it will be easy to generalize.
Clicker Question
What is wrong with the following derivation of a "rocket equation" for one-dimensional motion? Here \( m \) is the mass of the rocket, and \( v \) is its speed, as pictured above. \( P \) is the total momentum of the rocket/fuel system.
\[ \begin{aligned} dP/dt = 0 \\ \frac{d}{dt} (mv) = 0 \\ \frac{dm}{dt} v + m \frac{dv}{dt} = 0 \\ \Rightarrow \frac{dv}{dt} \stackrel{?}{=} -\frac{v}{m} \frac{dm}{dt} \end{aligned} \]
A. The first line is wrong: there is some force external to the rocket/fuel system.
B. The second line is wrong: \( P \) is not equal to \( mv \).
C. The third line is wrong: we can't distribute \( d/dt \) like that.
D. The fourth line is wrong: we made an algebra mistake somewhere.
Answer: B
The only plausible answers here are A and B: it's always correct to distribute a derivative with the product rule, and you can easily check that the algebra to get to line 4 is right. So one of the very basic assumptions is wrong: either momentum isn't conserved, or \( P = mv \) is wrong.
Why should \( P \) not be equal to \( mv \)? The problem is that \( m \) and \( v \) only refer to the rocket itself, not keeping track of the fuel of the rocket. The total momentum of rocket + fuel is definitely conserved, but then when we write \( P \) we have to include the fuel too! So the mistake is on line 2.
Let's work more carefully, which means starting with an inertial frame of reference (the rocket will accelerate, so its frame is no good.) What does an observer on the ground see, watching the rocket system? Let's set up some coordinates, considering both the rocket and an infinitesmal bit of mass \( dm \) being ejected, and just considering motion in a single direction \( x \):
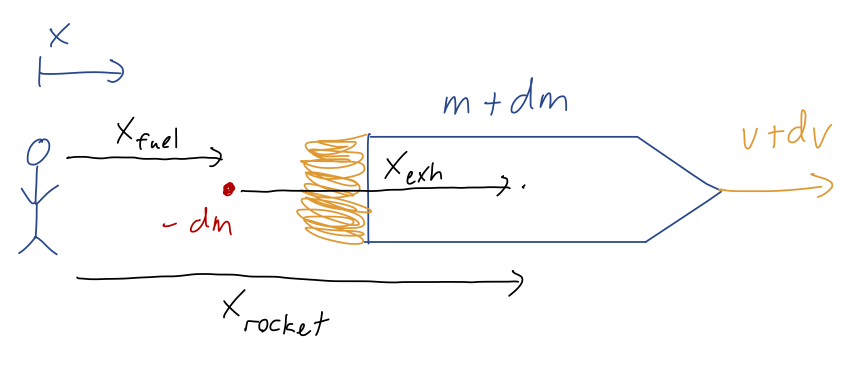
Just like the boat example, \( x_{\rm exh} = x_{\rm rocket} - x_{\rm fuel} \) is a redundant but useful coordinate describing the position of the bit of fuel \( dm \) relative to the rocket. Notice that we're writing the mass of the fuel as "\( -dm \)", which means \( dm \) itself is negative: this will give us \( dm/dt < 0 \) for the rocket itself, which it has to be since it's losing mass. (This is a little confusing here, but less confusing later!)
Clicker Question
Which is the correct equation for \( v_{\rm fuel} \), the speed of the fuel in the observer's frame of reference? Here \( v_{\rm exh} \), the exhaust speed, is always positive (it's a speed, not a velocity!)
A. \( v_{\rm fuel} = v_{\rm exh} + v_{\rm rocket} \)
B. \( v_{\rm fuel} = -v_{\rm exh} + v_{\rm rocket} \)
C. \( v_{\rm fuel} = v_{\rm exh} - v_{\rm rocket} \)
D. \( v_{\rm fuel} = -v_{\rm exh} - v_{\rm rocket} \)
Answer: B
Your intuition might be throwing you off on this one! If you imagine that \( v_{\rm fuel} \) has to be negative (moving backwards), you might be leaning towards C and D. But that doesn't have to be the case if \( v_{\rm rocket} \) is large enough!
Using the coordinates we've defined above actually makes this nice and easy: we have
\[ \begin{aligned} x_{\rm exh} + x_{\rm fuel} = x_{\rm rocket} \\ \vec{v}_{\rm exh} + \vec{v}_{\rm fuel} = \vec{v}_{\rm rocket} \\ \vec{v}_{\rm fuel} = -\vec{v}_{\rm exh} + \vec{v}_{\rm rocket} \end{aligned} \]
Now we have to be careful with the difference between velocity and speed, since \( v_{\rm exh} = |\vec{v}{\rm exh}| \) might have an extra minus sign. Let's look at the coordinates as we drew them: we expect that as the fuel moves away from the rocket, \( dx{\rm exh} / dt > 0 \), that is, \( x_{\rm exh} \) is increasing. This means that \( \vec{v}_{\rm exh} \) is already positive, so the speed doesn't have an extra minus sign; we find B as the final answer.