Let's continue with the rocket system we set up last time:
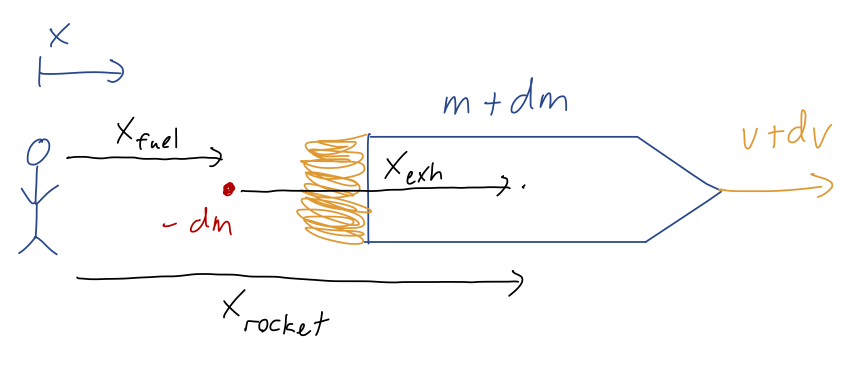
For the rest of this derivation, I'll write the relationship between the speeds as
\[ \begin{aligned} v_{\rm fuel} = -|v_{\rm exh}| + (v + dv) \end{aligned} \]
keeping the absolute value sign as a reminder that \( v_{\rm exh} \) is a speed.
By the way, we can check a couple of other limits to make sure that we have everything right here. Ignoring the tiny change \( dv \), if \( v=0 \), we see that \( v_{\rm fuel} = -|v_{\rm exh}| \) - if the rocket and the observer are both at rest with respect to each other, then from either perspective it looks like the fuel is coming out at the exhaust speed, to the left. If instead \( v = +|v_{\rm exh}| \), then \( v_{\rm fuel} = 0 \). If the rocket is moving right at exactly the exhaust speed, then the fuel looks like it's at rest when ejected, according to the ground observer. (Convince yourself that this makes sense!)
Now we apply conservation of momentum:
\[ \begin{aligned} \vec{P}(t) = \vec{P}(t+dt) \\ mv = p_{\rm fuel} + p_{\rm rocket} \\ = (-dm) v_{\rm fuel} + (m+dm) (v + dv) \end{aligned} \]
Cancelling off the \( mv \) on both sides, this becomes
\[ \begin{aligned} 0 = (-dm) (-|v_{\rm exh}| + v + dv) + v dm + m dv \\ -|v_{\rm exh}| dm = m dv \end{aligned} \]
where a couple more cancellations have happened. Finally, we apply a time derivative:
\[ \begin{aligned} m \frac{dv}{dt} = -|v_{\rm exh}| \frac{dm}{dt}. \end{aligned} \]
This is the rocket equation, which will let us calculate the motion of the rocket. Remember, the rocket is losing mass, so \( dm/dt < 0 \), which means that \( dv/dt > 0 \), i.e. the rocket moves forwards. Since this ends up looking exactly like Newton's second law, we can identify the right-hand side as a force, called the thrust:
\[ \begin{aligned} \vec{F}_{\rm thrust} = -|v_{\rm exh}| \frac{dm}{dt} \end{aligned} \]
For a rocket to achieve larger thrust, we see that either the reaction has to be faster (so \( |dm/dt| \) goes up), or more energetic (so \( |v_{\rm exh}| \) goes up.)
In general, we could have a rocket where the exhaust speed is a function of time. However, if it is constant, we can easily integrate to find the motion. It's slightly more general to do this by cancelling the \( dt \)'s off again, rewriting the rocket equation as
\[ \begin{aligned} -\frac{dv}{|v_{\rm exh}|} = \frac{dm}{m} \\ v(m) = -|v_{\rm exh}| \ln m + C \end{aligned} \]
Using the generic initial condition that \( v(m_0) = v_0 \), we have
\[ \begin{aligned} C = v_0 + |v_{\rm exh}| \ln m_0 \\ \Rightarrow v(m) = v_0 + |v_{\rm exh}| \ln (m_0/m). \end{aligned} \]
Since this relates \( v \) to \( m \) directly, this is true whether or not \( dm/dt \) is constant. (If \( dm/dt \) is constant, then we have constant thrust and we can just find \( m(t) \) and then integrate with respect to time.)
The bad news in this equation is that we have a logarithmic dependence on mass - this makes it very difficult to increase the top speed of our rocket by just adding more fuel! To be concrete, we can write
\[ \begin{aligned} m_0 = m_E + m_F \end{aligned} \]
where \( m_E \) is the mass of the empty rocket, and \( m_F \) is the mass of the fuel. (If you're looking up real-world information on rockets, \( m_E \) is often called the "dry mass", while the total \( m_E + m_F \) including the fuel is the "wet mass".) Then the top speed of the rocket, if it starts from rest, is
\[ \begin{aligned} v_{\rm max} = v(m_E) = |v_{\rm exh}| \ln \left( 1 + \frac{m_F}{m_E} \right) \end{aligned} \]
So if the exhaust velocity is fixed, just making our rocket bigger alone won't help; if we double the size of the rocket and both \( m_E \) and \( m_F \) are twice as large, the top speed doesn't increase at all! We need to either increase \( m_F \) without making the rocket heavier, or make \( m_E \) lighter with the same amount of fuel.
Even if we can accomplish those engineering feats, the gains are heavily diminishing. Suppose we build a rocket which has 90% of its mass devoted to fuel, so \(m_F = 10 m_E\). Then its top speed is about 2.4 times \(|v_{\rm exh}|\). If we somehow strip nearly all the mass out of the rocket and make a better design which is 99% fuel by mass, then \(m_F = 100 m_E\), but the top speed will only go up to 4.6 times \(|v_{\rm exh}|\). Physically, it's easy to see the problem: to get more total thrust we need more mass to eject, but if we start with more mass, then we get less speed for the same amount of thrust.
Example: rocket car
Suppose we have a rocket-powered car moving in a straight line across a flat surface. Ignoring friction and air resistance, how does the position of the car change with time?
As always we start with the equation of motion, which is
\[ \begin{aligned} m(t) \ddot{x} = F_{\rm thrust}. \end{aligned} \]
This looks simple, but we have to deal with the extra complication that \( m(t) \) is time dependent. Fortunately, since we know that the mass ejection rate is constant, it's easy to see that
\[ \begin{aligned} m(t) = m_0 - kt. \end{aligned} \]
Our equation of motion is nice and separable: moving things around and integrating, we find first that
\[ \begin{aligned} \int_{\dot{x}(0)}^{\dot{x}(t)} d\dot{x}' = F_{\rm thrust} \int_0^t \frac{dt'}{m_0 - kt'} \\ \dot{x}(t) = \dot{x}(0) - \frac{F_{\rm thrust}}{k} \ln \left(1 - \frac{kt}{m_0}\right). \end{aligned} \]
To get the position, we integrate one more time. A useful identity is
\[ \begin{aligned} \int dx \ln x = x \ln x - x \end{aligned} \]
(which you can easily check by taking the derivative!) Applying this to our result above, we see that (using \( u = 1 - (kt/m_0) \))
\[ \begin{aligned} \int dt\ \ln \left(1 - \frac{kt}{m_0} \right) = -\frac{m_0}{k} \int du \ln u \\ = -\frac{m_0}{k} (u \ln u - u) \\ = \left(\frac{m_0}{k} - t\right) \left[1 - \ln \left( 1 - \frac{kt}{m_0} \right) \right] \end{aligned} \]
Plugging back in, we end up with
\[ \begin{aligned} x(t) = x(0) + \left(\dot{x}(0) + \frac{F_{\rm thrust}}{k} \right) t + \frac{F_{\rm thrust} (m_0 - kt)}{k^2} \ln \left(1 - \frac{kt}{m_0}\right). \end{aligned} \]
This is an analytic solution, but it's already pretty complicated - and this was the simplest possible case, with no other forces acting! It's also worth noting that this solution is not valid for all times: mathematically, we can see that at \( t = m_0 / k \) the log blows up, and we have \( x(m_0 / k) \rightarrow \infty \)!
Of course, \( t = m0 / k \) is the time at which \( m(t) = 0 \), which is obviously not possible. Physically, we know that our solution is only valid until the fuel is burned completely, at which point \( F{\rm thrust} \) shuts off and we just have constant speed from that point on (the speed we already found with the rocket equation above, in fact.)
What if we have other external forces? If we wanted to track the motion of the rocket-exhaust system combined, we could keep track of the combined center of mass and see how the forces act on that. However, this would be complicated to do! Fortunately, we don't care about the combined system - we only care about the net forces on the rocket itself. So if we have additional forces like drag or gravity, we just treat them as acting on the rocket, in addition to the thrust force provided by the ejected mass.
For example, taking both forces above at once and assuming quadratic drag, a rocket moving vertically from the Earth's surface has the equation of motion
\[ \begin{aligned} m(t) \dot{v} = \vec{F}_{\rm thrust} - m(t) g - cv^2. \end{aligned} \]
although this will get more complicated quickly if we remember that the density of air depends strongly on altitude, so \( c = c(z) \) for a more realistic model (and at some point, \( g \) also depends on position.) This also means there's no terminal velocity for a rocket launch into space; once it gets out of the Earth's atmosphere and away from the Earth's gravity, the rocket will just continue to move at constant speed.
As you can start to see, getting much further with practical examples of rocketry is going to require a lot of additional details, and the equations will become difficult to handle very, very quickly. Basically, any realistic rocket problems are going to involve heavy use of numerical solutions. However, there's one more interesting example that we can do, which is to consider the idea of a multi-stage rocket.
Example: multi-stage rockets
A multi-stage rocket is just multiple rockets, stuck together. The rockets are burned one at a time, with the spent rockets being ejected after they are used up. For example, in a two-stage rocket the first stage is burned, then ejected, so that the second stage only has to propel itself and the cargo from that point:
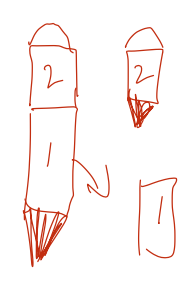
Ignoring all other forces (e.g. imagine we're working in deep space), let's compare the maximum speed of two different rockets. Rocket A is simple rocket with a fuel-to-mass ratio of \( m_{A,F} / m_{A,E} = 25 \). Rocket B is a two-stage rocket, which means it's two rockets stuck together: both stage 1 and stage 2 have a fuel-to-mass ratio of \( m_{B1,F} / m_{B1,E} = m_{B2,F} / m_{B2,E} = 10 \). Stage 2 is also about 5 times lighter than stage 1, i.e. \( m_{B1,E} / m_{B2,E} = 5 \). Assuming \( v_{\rm exh} = 2.5 \) km/s, what is the \( \Delta v \) supplied by each rocket?
We only need one equation here, although we'll need it a few times. From above, we can get the \( \Delta v \) for rocket A just by plugging in:
\[ \begin{aligned} (\Delta v)_A = |v_{\rm exh}| \log \left(1 + \frac{m_{A,F}}{m_{A,E}} \right) \\ = |v_{\rm exh}| \log \left(1 + 25 \right) = 8.1\ {\rm km} / {\rm s} \end{aligned} \]
Next time, we'll continue to find the delta-v for the two-stage rocket.