Last time, we were talking about getting force from potential, and found the equation
\[ \begin{aligned} \vec{F} = -\vec{\nabla} U \end{aligned} \]
with \( \vec{\nabla} U \) being the gradient of the potential \( U \).
One simple but important note about \( \vec{\nabla} \) is that it can be distributed over sums, i.e. if we have two different potential functions,
\[ \begin{aligned} \vec{\nabla} (U_1 + U_2) = \vec{\nabla} U_1 + \vec{\nabla}U_2. \end{aligned} \]
(In math terms, this corresponds to \( \vec{\nabla} \) being a linear operator.) This means that if we have two separate forces acting on an object, and we know each of their potential functions, then the total potential is just the sum of the individual ones. We already pointed this out before, but now it's clearly related to the fact that when we have multiple forces, we just add them as vectors.
Since this is a physics class, the most physical explanation for what \( \vec{\nabla} U \) means is (in my opinion) in terms of differentials, specifically the relation
\[ \begin{aligned} dU = \vec{\nabla} U \cdot d\vec{r}. \end{aligned} \]
In other words, if we sit at some point \( \vec{r} \) in space and then ask the question "how does \( U \) change if I move a tiny distance \( d\vec{r} \) in some direction?", the answer is encoded in the gradient \( \vec{\nabla} U(\vec{r}) \), which contains all of the directional derivatives of \( U \) at that point.
The differential version also gives us some nice insights into the meaning of \( \vec{\nabla} U \) as a vector. Suppose we sit at a single point, so \( \vec{\nabla} U \) is fixed, and then try to vary \( d\vec{r} \). We'll find that the largest dot product, and thus the largest \( dU \), occurs when \( d\vec{r} \) points in the \( \vec{\nabla} U \) direction. So \( \vec{\nabla} U \) points in the direction of the largest rate of change of \( U(\vec{r}) \).
We can also see that if \( \vec{\nabla} U = 0 \), then \( dU = 0 \) regardless of which direction we choose. So wherever \( \vec{\nabla} U = 0 \), the function \( U(\vec{r}) \) must be at a local extremum (maximum or minimum, or possibly a saddle point.)
One more extremely useful observation: going back to the general case where \( \vec{\nabla} U \neq 0 \), we can see that if we take \( d\vec{r} \) in the direction perpendicular to \( \vec{\nabla} U \), then \( dU = 0 \). If we keep traveling in the direction perpendicular to \( \vec{\nabla} U \), we will trace out a line along which \( U \) is constant. This line is known as an equipotential. In fact, for a given \( \vec{\nabla} U \) there is a whole plane of perpendicular vectors we can choose, which means that in three dimensions we actually have a two-dimensional equipotential surface along which \( U \) doesn't change.
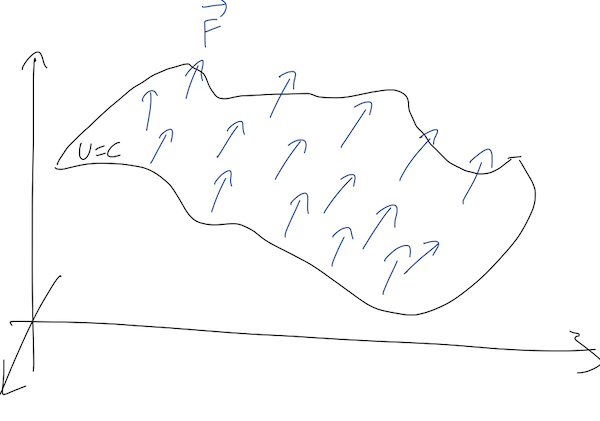
This gives us a useful way to visualize forces in two dimensions (the concept is still the same in three dimensions, but it's very hard to draw!) Consider a point particle moving in the \( (x,y) \) plane, subject to some unknown force. In two dimensions, equipotential surfaces will just be lines, so we can make a contour plot showing the lines of constant \( U \):
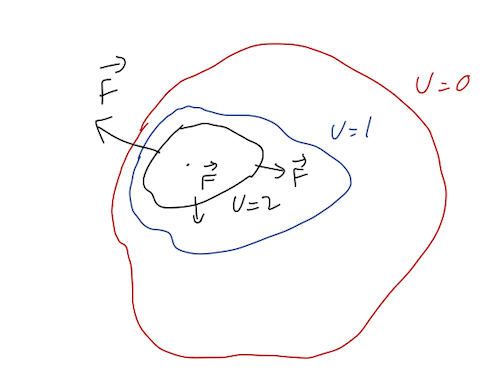
If you've ever read a topographic map, which shows lines of constant elevation in a top-down view, then you're used to reading equipotential plots:
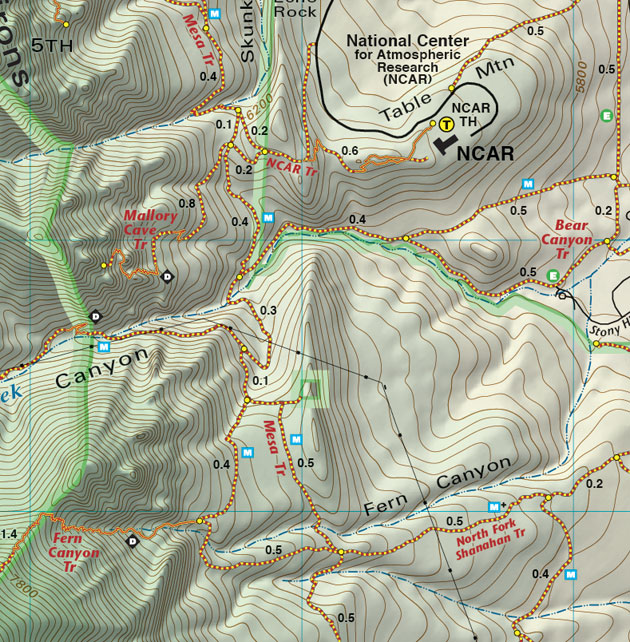
(source: https://www.latitude40maps.com/boulder-county-trails/)
Here the contours are equal height \( z \), but since the gravitational potential \( U(z) \propto z \), this is also a gravitational equipotential plot! This can give a useful metaphor for interpreting equipotential plots for other forces. In particular, it can help us remember the following facts:
- Equipotential lines never cross. This is basically true by definition: two different lines correspond to two different constant potential energies \( U_1 \) and \( U_2 \). Crossing would mean the potential can have two different values at the same point; our definition of a conservative force guarantees that can't be true. For the topographic map, this is obvious - one point can't have two heights!
- Force points "downhill". In general, this means that since \( \vec{F} = - \vec{\nabla} U \), the force is in the direction perpendicular to the equipotential lines and points towards smaller \( U \). (In the topographic plot, this is literally downhill.)
- Spacing of lines tells us the magnitude of \( |\vec{\nabla} U| \). Densely-spaced lines indicate that the potential is changing rapidly vs. position, indicating a large force. Again, this is intuitive for the topographic plot: lots of dense lines in a certain spot means a very steep slope.
Let's gain some intuition by thinking about the details of equipotentials like this.
Clicker Question
Here is an equipotential plot of some unknown potential function \( U(\vec{r}) \). The red curve is the contour corresponding to the largest value of \( U \) out of the contours shown. Looking at the blue X, which way does \( \nabla U \) point?
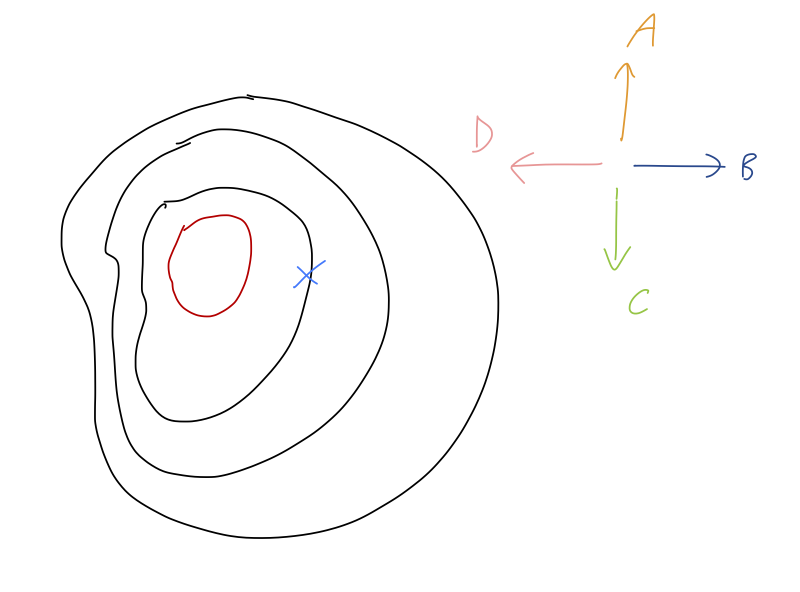
Answer: D
We know that \( \nabla U \) has to point in the direction where \( U \) is increasing most rapidly. Out of the given choices, we see that A and C are roughly pointing along the equipotential contour, where \( U \) is constant - so \( \nabla U \) can't be in those directions. Either B or D is pointing in a direction of rapid change in \( U \); using the fact that the red contour has larger \( U \) than the one with the X, the answer must be D.
Note that the force will point the other way, towards smaller values of \( U \), since \( \vec{F} = -\nabla U \). (Or in terms of energy, force is produced by conversion of \( U \) into \( T \), so it points in the direction where \( U \) decreases.) In the gravity analogy, the potential change \( \nabla U \) is largest "uphill", but the force points "downhill".
Clicker Question
On the same equipotential plot, at which point can the gradient \( \nabla U \) be equal to zero?
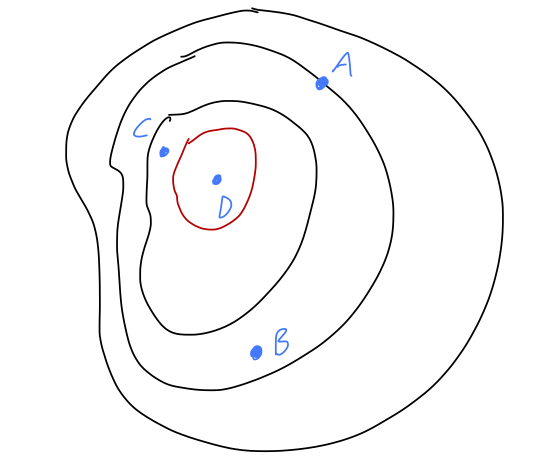
Answer: D
Remember that equipotential lines cannot cross! This means that if we continue to draw equipotentials inside the red curve, they must continue to get smaller and smaller until they converge on a single point. Moving in any direction from that point leads to a change in \( U \), which means that there is no direction to determine \( \nabla U \) - it must be zero. (If you recall your vector calculus, this is the statement that such a point is a local extremum of the function.) This is exactly point D.
We can also find the answer by elimination. Points B and C are sitting in between two equipotential contours; that means that we can change \( U \) by continuing towards the inner contour with larger \( U \), so \( \nabla U \) points in that direction and is not zero. Point A is sitting on an equipotential contour, which means there are directions we can move for which \( \Delta U = 0 \) (along the contour.) But this isn't the same as \( \nabla U \), which finds the direction of largest increase and will thus not point along the contour. For \( \nabla U \) to be zero, it must be true that \( U \) doesn't change in any direction we move.
Here's another example I've borrowed, showing equipotential contours for a pair of opposing electric charges:

(source: https://www.asc.ohio-state.edu/durkin.2/phys132/). This is not a plot of 3d equipotential surfaces: it's a two-dimensional plot (the bright lines are equipotential contours), with the third 'dimension' denoting the value of \( U(x,y) \).
Finally, you won't be surprised to learn that Mathematica has a function to make these plots for us, called ContourPlot[]. I won't dwell on the details, but here's a quick example showing how to make our own equipotential plot for a pair of electric charges.

Example: gradients and forces
As a quick example, suppose a particle has a potential energy function of the form
\[ \begin{aligned} U(x,y,z) = 3x \cos(y/L) - 2z^2 \end{aligned} \]
(ignoring units for now, this is a math exercise.) What is the force?
To find the force, we take the gradient: \( \vec{F} = -\vec{\nabla} U \). For the gradient, we need to know the partial derivatives of \( U \) with respect to all three coordinates. We haven't done any partial derivatives yet this semester, so let's go through them:
\[ \begin{aligned} \frac{\partial U}{\partial x} = 3 \cos (y/L) \\ \frac{\partial U}{\partial y} = -\frac{3x}{L} \sin (y/L) \\ \frac{\partial U}{\partial z} = -4z \end{aligned} \]
(finding partial derivatives is easy: we just ignore everything that we're not taking a derivative of.) Thus, the force is
\[ \begin{aligned} \vec{F} = -\vec{\nabla} U \\ = -\frac{\partial U}{\partial x} \hat{x} - \frac{\partial U}{\partial y} \hat{y} - \frac{\partial U}{\partial z} \hat{z} \\ = -3 \cos (y/L) \hat{x} + \frac{3x}{L} \sin (y/L) \hat{y} + 4z \hat{z}. \end{aligned} \]
Curl and Stokes' theorem
The operator \( \vec{\nabla} \) can be used to define other useful quantities, in addition to the gradient. One of these useful quantities is called the curl, where the curl of \( \vec{v} \) is denoted by \( \vec{\nabla} \times \vec{v} \). The cross product here is taken literally: the definition of curl is that we take the cross product of the gradient vector with the second vector. You'll remember that one way to write the cross product is using a 3x3 determinant; using this notation here, the curl is (in Cartesian coordinates only!)
\[ \begin{aligned} \nabla \times \vec{v} = \left|\begin{array}{ccc} \hat{x}&\hat{y}&\hat{z}\\ \frac{\partial}{\partial x}&\frac{\partial}{\partial y}&\frac{\partial}{\partial z}\\ v_x&v_y&v_z\end{array}\right| \\ = \left( \frac{\partial v_z}{\partial y} - \frac{\partial v_y}{\partial z} \right) \hat{x} + \left( \frac{\partial v_x}{\partial z} - \frac{\partial v_z}{\partial x} \right) \hat{y} + \left( \frac{\partial v_y}{\partial x} - \frac{\partial v_x}{\partial y} \right) \hat{z}. \end{aligned} \]
Now suppose we have a force \( \vec{F} \) which is conservative. By definition, that means we can find a potential function \( U \) so that \( \vec{F} = -\vec{\nabla} U \). But now notice what happens when we try to take the curl of \( \vec{F} \) and write it in terms of \( U \):
\[ \begin{aligned} (\vec{\nabla} \times \vec{F})_x = \frac{\partial F_z}{\partial y} - \frac{\partial F_y}{\partial z} \\ = \frac{\partial}{\partial y} \left( -\frac{\partial U}{\partial z} \right) - \frac{\partial}{\partial z} \left( -\frac{\partial U}{\partial y} \right). \end{aligned} \]
But the order of partial derivatives doesn't matter: there's only one \( \partial^2 U / \partial y \partial z \), so both terms are the same. Therefore, \( (\vec{\nabla} \times \vec{F})_x = 0 \). Of course, we didn't assume anything special about the \( x \)-direction, so it won't surprise you to know that the whole curl is in fact zero! We've just proved the vector identity
\[ \begin{aligned} \vec{\nabla} \times \vec{\nabla} U = 0 \end{aligned} \]
for any function \( U \). This means that if we have a conservative force, then its curl must be zero:
\[ \begin{aligned} \vec{\nabla} \times \vec{F} = 0. \end{aligned} \]
Curl looks like kind of a weird and arbitrary quantity, so you might wonder why we care if a force has zero curl or not. The short answer is that this identity goes both ways: if we're given a force \( \vec{F} \), we can calculate its curl, and if it is equal to zero then the force must be conservative. So curl allows us to test for a conservative force!
This is a big deal, because you'll remember that the second condition for a force to be conservative was that work done is independent of path, which is something you definitely can't test directly - there are always an infinite number of paths. But we argued that the path-independence of work is equivalent to the condition that
\[ \begin{aligned} \oint \vec{F} \cdot d\vec{r} = 0, \end{aligned} \]
i.e. the work vanishes on any closed path (a path that goes back to the same point, i.e. a loop.) But now we come to an important vector calculus result, Stokes' theorem, which I will state but not prove:
\[ \begin{aligned} \oint_{\partial \mathcal{S}} \vec{F} \cdot d\vec{r} = \int \hspace{-4mm} \int_{\mathcal{S}} (\vec{\nabla} \times \vec{F}) \cdot d\vec{A} \end{aligned} \]
Those are some pretty dense symbols, so in words: "Consider a finite surface \( \mathcal{S} \), with boundary curve \( \partial S \). The surface integral of the curl of any vector over \( \mathcal{S} \) is equal to the line integral of the same vector around the boundary \( \partial S \)."
We don't need to go too deep into surface integrals for our current purposes; as the name implies, they are the two-dimensional equivalent of a line integral. The important point right now is that if we have a force for which the curl \( \vec{\nabla} \times \vec{F} \) vanishes, then its line integral around any closed loop anywhere is automatically zero by Stokes' theorem. So there are several equivalent ways to state that a force \( \vec{F} \) is conservative:
- If the work done is path-independent;
- If \( \vec{F} = -\vec{\nabla} U \) for some function \( U \);
- If \( \vec{\nabla} \times \vec{F} = 0 \) everywhere.
Curl is much more important in electrodynamics; in mechanics, it's mostly important as a test for conservative forces. We'll have significantly more use for the divergence \( \vec{\nabla} \cdot \vec{F} \) later on, but for now let's simply move on to our next topic.
Energy and one-dimensional systems
Although we've been working a lot in three dimensions with our vector calculus proofs, it turns out that some of the most powerful features of energy conservation arise in one-dimensional systems. It should be noted that "one-dimensional" here doesn't mean "only moving along a line"; it refers to any physical system in which we only need a single coordinate to tell us the full state of the system.
A basketball in freefall with no horizontal motion is a one-dimensional system (we just need the height \( y \)), but so is a pendulum (just need the angle \( \theta \)), or even a roller coaster (it's stuck on a track, so we can describe it in terms of \( s \), the distance along the track.) For simplicity, we'll call our single coordinate \( x \) in the following.
What about conservative forces? Taylor shows that because one-dimensional "paths" are very simple, any force which only depends on position is automatically conservative in one dimension. So as long as there's no dependence on other parameters like speed or time, any force in one dimension has a corresponding potential energy \( U(x) \), and
\[ \begin{aligned} F(x) = -\frac{dU}{dx}. \end{aligned} \]
Next time: more on one-dimensional systems.