Continuing from the clicker question from last time:
Clicker Question
Continuing with the observer sitting at point \( (0,0,z) \) above the origin, based on symmetry, what must be true about the components of the force \( \vec{F}_g \) due to the line charge?
A. There is no \( F_x \).
B. There is no \( F_y \).
C. There is no \( F_z \).
D. There is no \( F_x \) or \( F_y \).
E. There is no \( F_x \) or \( F_z \).
Answer: D
This is very similar to the last question, but there is a subtle and important difference in vector components vs. coordinate dependence. The best way to think about this question for gravity specifically is to write out the formula in components:
\[ \begin{aligned} \vec{F}_g = \frac{-GMm}{r^3} \vec{r} = \frac{-GMm}{r^3} (x \hat{x} + y \hat{y} + z \hat{z}). \end{aligned} \]
Remember that these coordinates are relative to the source. Since we're sitting on the axis at \( y=0 \), and since the entire line charge is also at \( y=0 \), the \( \hat{y} \) contribution is always zero so there is no \( F_y \).
The \( \hat{x} \) component, meanwhile, will be proportional to \( x \). For every point on the line at \( +x \), there is another point at \( -x \) which has the same \( r \) and thus gives an equal and opposite contribution. So all of the \( \vec{F}_g \) contributions cancel, and \( F_x \) is also zero, leading us to answer D. (There is a \( z \) component, since the entire line contributes without cancellation in that direction - \( z \) is always the same sign!)
These arguments rely on the specifics of gravity as a conservative central force. However, there's actually a much more powerful way to show that \( F_x \) and \( F_y \) have to be zero for any force provided by a line of charges. The argument is surprisingly simple: suppose that there is some non-zero \( F_x \) and \( F_y \). Then the force vector is pointing in some direction in the \( x-y \) plane. Now suppose the observer turns around by 180 degrees in that plane: they'll be unable to tell anything is different, since the world looks exactly the same to them. So whatever \( F_x \) and \( F_y \) are, they must be the same. But turning around 180 degrees will flip both \( F_x \) and \( F_y \) (from the observer's perspective), so they must change to \( -F_x \) and \( -F_y \). This is a contradiction, unless both of those components are zero!
Clicker Question
Consider a set of five identical masses \( m \), arranged in a pentagon configuration. What is the force of gravity on a test mass at the exact center of the pentagon?
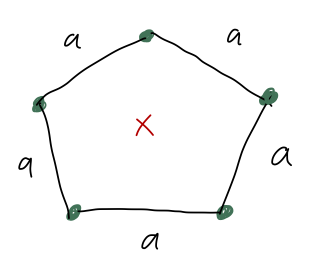
A. Zero
B. Non-zero
C. We'll need a calculator to tell whether zero or non-zero!
Answer: A
This answer is probably intuitive, but actually arguing it is trickier than it looks! We can try to begin with cancellation of vector components: in the \( \hat{x} \) direction we identify two pairs of equal and opposite contributions to \( g_x \), whereas the fifth point at the top is at \( x=0 \) and so can't contribute to \( g_x \). Thus, we see right away that at least \( g_x = 0 \).
However, we can't do the same simple argument for \( g_y \); here the situation is imbalanced, with three masses on one side and two on the other. But as I've hinted at by putting this question after the last two, there's a symmetry argument that we can use! This time, the symmetry is rotational.
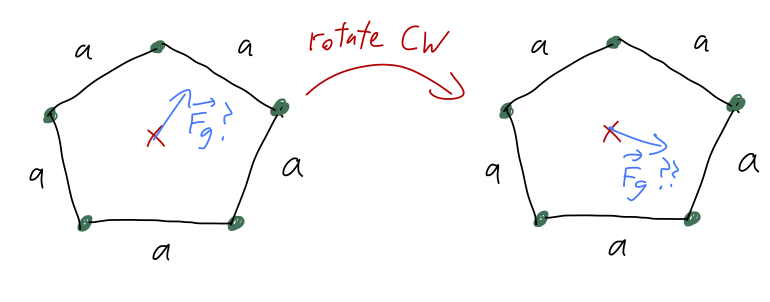
Exactly as with the line charge before, if we imagine our observer at the X rotating around by 72 degrees, they see no change at all to the world around them. But if we assume there is any non-zero \( \vec{F}_g \), it has to rotate with the observer - but it also can't rotate, since if the masses are in the same place the answer must be the same! Thus, by contradiction \( \vec{F}_g \) must be zero.
Gravitation and extended sources
To deal with realistic objects, we'd like to be able to calculate the gravitational field due to a continuous object with some density. Recalling our previous example of finding the center of mass, we can think of this as just adding up all of the contributions from infinitesmal bits of mass \( dm \) inside of an object. For the center of mass, recall we had
\[ \begin{aligned} M = \sum_\alpha m_\alpha,\ \ \vec{R} = \frac{1}{M} \sum_\alpha m_\alpha \vec{r}_\alpha \end{aligned} \]
which became for continuous objects
\[ \begin{aligned} M = \int dm = \int \rho(\vec{r}) dV,\\ \vec{R} = \frac{1}{M} \int \vec{r} dm = \frac{1}{M} \int \vec{r} \rho(\vec{r}) dV. \end{aligned} \]
Similarly, for an extended massive source, we can add up all of the contributions to the gravitational field from individual pieces. However, this is going to be a little more complicated, so we should start with a diagram:
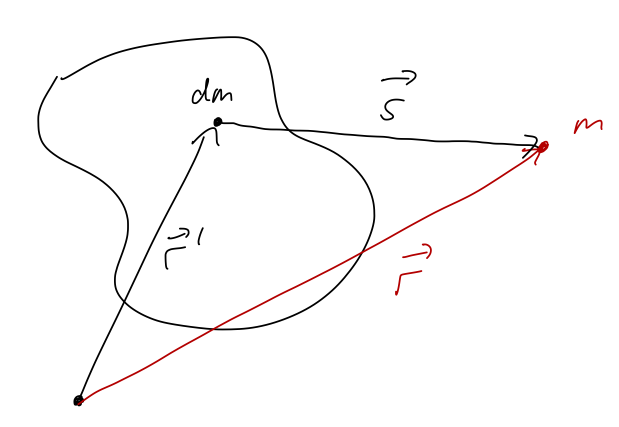
As pictured, we have to keep track of the location \( \vec{r}' \) of our source mass, but also the position \( \vec{r} \) where we want to know the field. As a sum over individual masses \( m_\alpha \), we have
\[ \begin{aligned} \vec{g} = \sum_\alpha -\frac{Gm_\alpha}{|\vec{s}_\alpha|^2} \hat{s}_\alpha \end{aligned} \]
where \( \vec{s} = \vec{r} - \vec{r}'_\alpha \) is the vector pointing from the source mass \( \alpha \) to the position \( \vec{r} \). (Some books will refer to this using a funny-looking script \( r \); I think this is confusing, and I also don't know how to typeset the weird \( r \), so I'll use \( s \).)
We find the continuous version by replacing \( m \) with the density \( \rho \):
\[ \begin{aligned} \vec{g}(\vec{r}) = -G \int \frac{dm}{|\vec{s}|^2} \hat{s} \\ = -G \int \frac{dV' \rho(\vec{r}')}{|\vec{r} - \vec{r}'|^3} (\vec{r} - \vec{r}') \end{aligned} \]
where I've written out \( \hat{s} \) in terms of the other vectors, which gives us an extra factor of \( 1/|\vec{s}| \). As the prime on \( dV' \) indicates, we're integrating over all possible positions \( \vec{r'} \) of the source mass \( dm \). We can do a \( u \)-substitution to think of the integral as being over the relative position vector \( \vec{s} \), but that hides the dependence on \( \vec{r} \) which is important to keep in mind.
This looks pretty horrible compared to the center of mass integral! Much of the complication comes from the fact that we have a second vector \( \vec{r} \) in addition to the one that we're trying to integrate over. We'll do a couple of examples, but I'll emphasize from the start that it is very important to make sketches and think carefully about these vectors when trying to calculate \( \vec{g} \)!
Symmetry will also be very useful, as with the center of mass. In particular, suppose we are at the origin and there are two equal pieces of mass at \( +\vec{s} \) and \( -\vec{s} \), exactly on opposite sides:
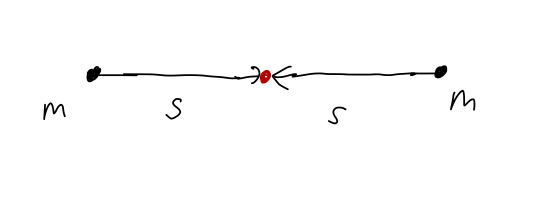
Then the total gravitational field is
\[ \begin{aligned} \vec{g} = -\frac{Gm}{s^2} \hat{s} - \frac{Gm}{s^2} (-\hat{s}) = 0. \end{aligned} \]
In other words, just as we saw for the CM position, the contributions of two equal masses at opposite positions to the \( \vec{g} \) field cancel exactly. This reflection-symmetry observation will extend to a whole object: if we have two solid hemispheres with the same mass and shape, then at the point exactly in between their centers, \( \vec{g} = 0 \) without having to calculate anything.
This can also work component by component. If we have our two equal masses at \( (+x',0,0) \) and \( (-x',0,0) \), and we're interested in the gravitational field along the \( y \) axis:
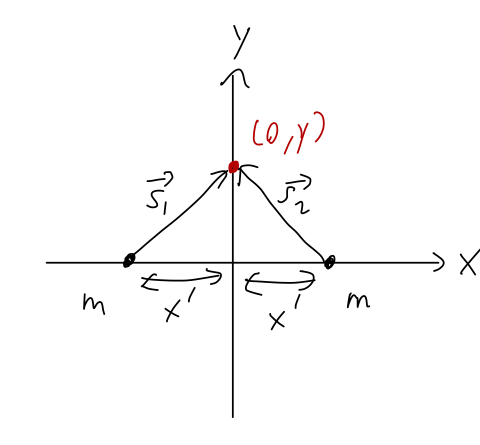
then we have
\[ \begin{aligned} \vec{g} = -\frac{Gm}{(x^2 + y^2)^{3/2}} (x\hat{x} + y \hat{y}) - \frac{Gm}{(x^2 + y^2)^{3/2}} (-x \hat{x} + y \hat{y}) \end{aligned} \]
writing out the unit vectors in our \( x,y \) coordinates. So in the \( x \)-direction, we have an exact cancellation again, and \( g_x = 0 \). However, we still have a contribution in the \( y \)-direction:
\[ \begin{aligned} \vec{g} = -\frac{2Gmy}{(x^2 + y^2)^{3/2}} \hat{y}. \end{aligned} \]
(The system isn't symmetric in this direction - it would be if there was another pair of charges a distance \( 2y \) up the \( \hat{y} \) axis.) This will give us a messy equation of motion, thanks to the \( 3/2 \) power in the denominator! But we can at least see that the force is always attractive towards \( y=0 \), as we might guess, so if we release a point particle somewhere on the \( y \)-axis, we would expect it to just oscillate back and forth along the \( y \)-axis. (In fact, this is a perfect case for a one-dimensional potential analysis!)
Before we move on to examples, one comment about the definition of \( dm \). The replacement we've used above is only really appropriate for three-dimensional objects, for which it makes sense to talk about the "volume" of the object. But we'll see a number of examples where we're interested in objects that don't really have volume, because they're flat (two-dimensional) or thin lines (one-dimensional.) We can handle these various cases by adjusting the form of \( dm \):
\( dm = \rho(\vec{r}) dV \) (solid object, 3-d)
\( dm = \sigma(\vec{r}) dA \) (flat object, 2-d)
\( dm = \lambda(\vec{r}) ds \) (linear object, 1-d)
Here \( \rho, \sigma, \lambda \) are all forms of "density", but with different units, for example \( \sigma \) (the "area density") has units of kg / m\( ^2 \), while \( \lambda \) (the "linear density") has units of kg / m.
Let's think a bit more about uses of symmetry with a couple more interesting problems.
Example: gravitational field of a disk
Let's try to apply our setup to a real example of finding \( \vec{g} \) for an extended object (not just point masses.) Suppose we have a solid but very thin disk of constant area mass density \( \sigma \) and radius \( R \).
To deal with a thin disk, our integral over \( dV \) will become just a two-dimensional area integral \( dA \), since the \( z \)-direction is infinitesmally thin. (If you're not happy with this hand-waving approximation, you can calculate the three-dimensional version of this for a height \( h \), and then take the limit \( h \rightarrow 0 \). You should get the same results we're about to find.)
Now, as with the center of mass, we can view the equation for \( \vec{g} \) as just three separate integrals to do for each of the components \( g_x, g_y, g_z \). In general, we need to calculate all three of them, but symmetry can save us by telling us certain components are automatically zero. However, things are complicated by the fact that we have to choose the point \( \vec{r} \) to calculate the field at. For a completely arbitrary point in space, symmetry won't help us for the disk!
But let's say we want to calculate the field directly above the center of the disk, along the \( z \)-axis:
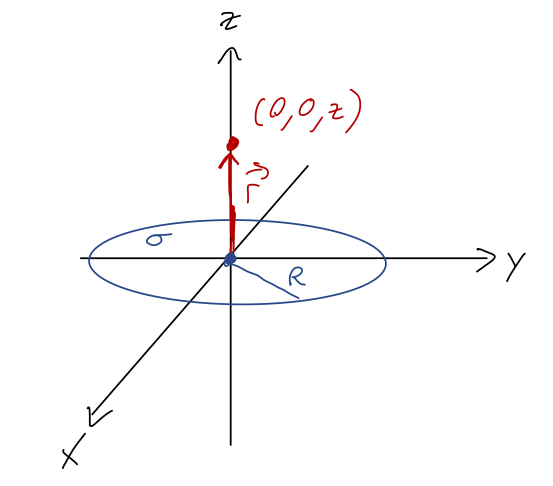
Then we have \( \vec{g}_x = \vec{g}_y = 0 \) thanks to reflection symmetry (remember, it's the reflection of the relative \( \vec{s} \) vector that matters, which is why we had to specify \( \vec{r} = z\hat{z} \) first!) Let's convince ourselves by actually setting up one of the integrals:
\[ \begin{aligned} g_x = -G \int \frac{dA' \sigma}{|\vec{r} - \vec{r}'|^3} (\vec{r} - \vec{r}')_x \\ = G \sigma \int \frac{dA' x'}{(x'^2 + y'^2 + z^2)^{3/2}} \end{aligned} \]
using \( \vec{r} - \vec{r}' = -x' \hat{x} - y' \hat{y} + z \hat{z} \), from the diagram. Now, this is already good enough to see the cancellation: because the integrand has a single \( x' \) upstairs, for every point on the disk at \( (+x', +y') \) there will be an equal and opposite contribution from \( (-x',y') \), so the whole thing will be zero. To see it even more explicitly, we should really change to cylindrical coordinates \( (\rho', \phi') \) inside the integral:
\[ \begin{aligned} g_x = G \sigma \int_0^{2\pi} d\phi' \int_0^R d\rho' \frac{\rho'^2 \cos \phi'}{(\rho'^2 + z^2)^{3/2}} \end{aligned} \]
The \( \phi' \) integral is the one that matters, and it's easy to do: we have
\[ \begin{aligned} \int_0^{2\pi} d\phi' \cos \phi' = \left. \sin \phi'\right|_0^{2\pi} = 0. \end{aligned} \]
Since the choice of \( x \)-direction vs. \( y \)-direction on a disk is totally arbitrary, clearly the same setup will give us \( g_y = 0 \) as well.