Continuing with the thin circular ring example from last time:
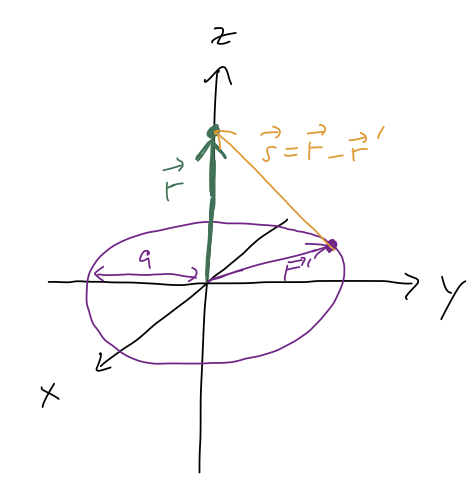
We calculated the mass as a warm-up, finding
\[ \begin{aligned} M = \int_0^{2\pi} d\phi' a \lambda = 2\pi a \lambda. \end{aligned} \]
Now on to the potential integral:
\[ \begin{aligned} \Phi(\vec{r}) = -G \int \frac{dm}{|\vec{r} - \vec{r}'|} = -G \int_0^{2\pi} \frac{a \lambda d\phi'}{|\vec{r} - \vec{r}'|}. \end{aligned} \]
To continue with the integral, we need to simplify the denominator. Fortunately, in cylindrical coordinates the two vectors are easy to write down:
\[ \begin{aligned} \vec{r} = z \hat{z} \\ \vec{r}' = a \hat{\rho}' \end{aligned} \]
so the difference is \( \vec{r} - \vec{r}' = z \hat{z} - a \hat{\rho}' \), and the length is simply \( \sqrt{z^2 + a^2} \). Thus, the integral becomes
\[ \begin{aligned} \Phi(z) = -G \int_0^{2\pi} \frac{a \lambda d\phi'}{\sqrt{z^2 + a^2}} \\ = \frac{-2\pi \lambda a G}{\sqrt{z^2 + a^2}} = -\frac{GM}{\sqrt{z^2 + a^2}}. \end{aligned} \]
Notice how much easier this was than integrating to get the force - only one integral instead of three! We do have one last step to get to the gravitational field (and thus the force), which is taking a gradient, but that will be simple:
\[ \begin{aligned} \vec{g} = -\nabla \Phi(z) \\ = \frac{GM}{(z^2 + a^2)^{3/2}} (2z) (-1/2) \hat{z} \\ = -\frac{GMz}{(z^2 + a^2)^{3/2}} \hat{z}. \end{aligned} \]
This always points towards the ring thanks to the \( z \) in the numerator, so the direction is what we expect. As a further check, we notice that if we go very far away from the ring so that \( z \gg a \), then we have \( z^2 + a^2 \approx z^2 \), and the force becomes
\[ \begin{aligned} \vec{g} \rightarrow -\frac{GMz}{(z^2)^{3/2}} = -\frac{GM}{z^2} \end{aligned} \]
as we would expect for a point particle. (It should make intuitive sense that if we're really far from the ring, it "looks" like a point source and we get the simple result. We'll come back to this point with more rigor soon.)
Example: gravitational potential of a sphere
Let's find the \( \vec{g} \) field due to a sphere of constant mass density \( \rho \), using the gravitational potential \( \Phi \). Once again, let's assume we're working along the \( z \)-axis, so \( \vec{r} = z\hat{z} \).
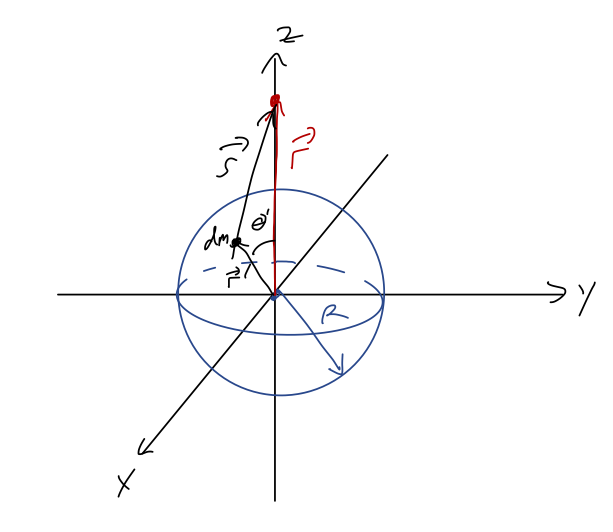
We start by setting up the integral, using the sketch as a guide:
\[ \begin{aligned} \Phi(\vec{r}) = -G \int \frac{dV' \rho}{|\vec{r} - \vec{r}'|}. \end{aligned} \]
Let's work in spherical coordinates since we have a sphere. We can re-express the denominator as
\[ \begin{aligned} |\vec{r} - \vec{r}'|^2 = (r' \sin \theta' \cos \phi')^2 + (r' \sin \theta' \sin \phi')^2 + (z - r' \cos \theta')^2 \\ = r'^2 + z^2 - 2zr'\cos \theta' \end{aligned} \]
(you may remember this as an example of the law of cosines), so then
\[ \begin{aligned} \Phi(z) = -G\rho \int_0^{2\pi} d\phi \int_0^R dr' \int_0^{\pi} d\theta' \frac{r'^2 \sin \theta'}{\sqrt{r'^2 + z^2 - 2zr' \cos \theta'}} \end{aligned} \]
This integral is surprisingly tricky, and is one of the first examples we've encountered where you'll run into a horrible mess if you try to brute force it in Mathematica! There's a very, very useful change of variables that we can make here. Let's define the distance \( s \) as before to be
\[ \begin{aligned} s^2 = |\vec{r} - \vec{r}'|^2 = r'^2 + z^2 - 2zr' \cos \theta'. \end{aligned} \]
Let's suppose that we're holding \( r' \) fixed and just treating \( \theta' \) as a variable. (As long as we do the \( \theta' \) integral first, this is perfectly valid!) Then differentiating both sides gives the much simpler result
\[ \begin{aligned} 2s ds = 2zr' \sin \theta' d\theta' \\ \Rightarrow r' \sin \theta' d\theta' = \frac{s}{z} ds \end{aligned} \]
which lets us rewrite the integral as, doing the \( \phi \) integral since nothing else depends on it,
\[ \begin{aligned} \Phi(z) = -2\pi G \rho \int_0^R dr' \int_{s_{\rm min}}^{s_{\rm max}} r' ds (s/z) \frac{1}{s} \\ = -\frac{2\pi G \rho}{z} \int_0^R dr' r' (s_{\rm max} - s_{\rm min}). \end{aligned} \]
To continue, we need to find the limits of integration on \( s \). These values started out as limits of integration on \( \theta' = 0,\pi \), which we can just plug in:
\[ \begin{aligned} s_{\rm min}^2 = r'^2 + z^2 - 2zr' = (r' - z)^2 \\ s_{\rm max}^2 = (r' + z)^2 \end{aligned} \]
Now, \( s_{\rm min} \) and \( s_{\rm max} \) are both distances, so they have to be positive. So \( s_{\rm max} = r' + z \), always. However, for the other limit, the answer depends on what \( z \) is. If \( z > r' \), then we have \( s_{\rm min} = z-r' \), otherwise it's equal to \( r'-z \). Let's assume that \( z > R \), i.e. we're looking for the potential outside the sphere. Then we have
\[ \begin{aligned} \Phi(z) = -\frac{2\pi G \rho}{z} \int_0^R dr' r' [(r'+z) - (z-r')] \\ = -\frac{2\pi G \rho}{z} \int_0^R dr' 2r'^2 \\ = -\frac{4\pi G \rho}{3z} R^3. \end{aligned} \]
Some of these numerical factors should look familiar: the combination \( 4\pi R^3/3 \) is just the volume \( V \) of the sphere, and since \( V \rho = M \), we have finally
\[ \begin{aligned} \Phi(z) = -\frac{GM}{z}. \end{aligned} \]
An important observation to make is that there is nothing special about the \( z \) direction for a sphere. If I chose a point in any arbitrary direction above the surface of the sphere to find the potential at, I could have just called that direction \( z \) and I would get the same answer.
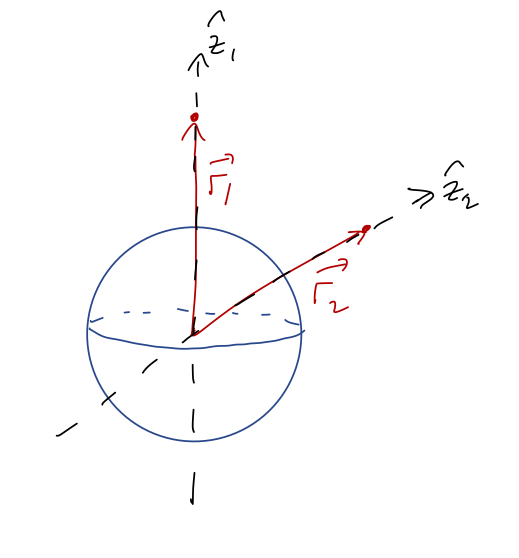
Thanks to this rotational symmetry, the \( z \)-axis answer is the answer everywhere: for any point a distance \( r>R \) from the center of the sphere, we have
\[ \begin{aligned} \Phi(r) = -\frac{GM}{r}. \end{aligned} \]
This is the same potential as if all of the mass were concentrated at the center of the sphere - even if we're really close to the surface!
Before we move on, I want to re-interpret some of the calculation we just did in more geometric terms. First of all, we replaced the spherical angle \( \theta' \) with the distance \( s \). But there's another angle hanging around, which is \( \phi' \), the polar angle. We just did that integral since nothing depends on it, thanks to the symmetry of the sphere. Implicitly, this means that after the \( \phi' \) integral we can think of the variable \( s \) as really pointing to an infinitesmal ring, not a point:
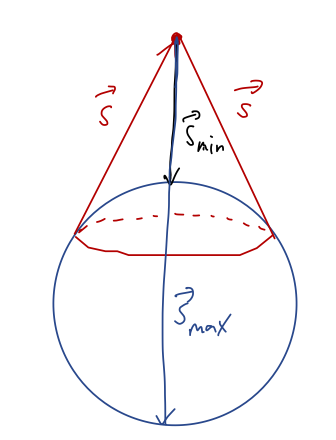
(This diagram should make the values of \( s_{\rm min} = z-r' \) and \( s_{\rm max} = z+r' \) we found above obvious!) Next we remember that \( s \) is not independent of \( r' \) - hence the order of integration. The ring traced out by \( \vec{s} \) depends on \( \theta' \), but it also depends on \( r' \): smaller distances from the sphere's center will trace out smaller rings. At fixed \( r' \), we can think of an integral over \( ds \) as describing an infinitesmal spherical shell. This opens up another way to think of what we're doing physically.
With that motivation, let's move to another closely related example: what is \( \Phi(z) \) inside of a hollow spherical shell? To solve for the thin spherical shell instead of the full sphere, let's go back to the following formula:
\[ \begin{aligned} \Phi(z) = \int_0^R dr' \int_{s_{\rm min}}^{s_{\rm max}} -\frac{2\pi G \rho(r') r' ds}{z} \end{aligned} \]
This is still perfectly valid for the spherical shell; the only difference is that instead of being a constant, the density \( \rho(r') \) will be zero everywhere except very close to \( r'=R \). As a result, we can use an approximation to get rid of the \( r' \) integral,
\[ \begin{aligned} \int_0^R dr' \rho(r') r' \approx \int_{R-\epsilon}^R dr' \rho r' \\ = \left. \frac{1}{2} \rho r'^2 \right|_{R-\epsilon}^R \\ = \frac{1}{2} \rho \left[ R^2 - (R - \epsilon)^2 \right] \\ = \frac{1}{2} \rho \left[ 2R \epsilon \right] \\ = \rho R \epsilon \end{aligned} \]
where we're stuck with the thickness \( \epsilon \) of the shell, but we'll get rid of that shortly. For now, we're left with
\[ \begin{aligned} \Phi(r) = -2\pi G \int_{s{\rm min}}^{s_{\rm max}} ds\ \frac{\rho R \epsilon}{z} \\ = -2\pi G \rho \frac{R}{z} \epsilon (s_{\rm max} - s_{\rm min}). \end{aligned} \]
Outside the shell we had \( s_{\rm min} = z-R \) and \( s_{\rm max} = z+R \), but now that we're inside the shell, we need to be more careful. Let's draw a sketch again:
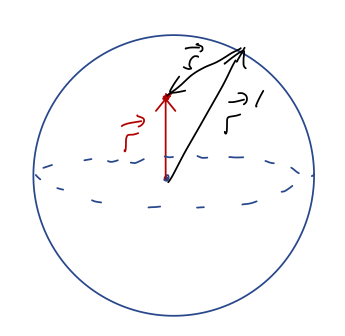
From the diagram, we know that \( s_{\rm max} = R + z \). However, unlike the previous calculation we now have \( s_{\rm min} = R - z \), with the opposite sign since \( z \) is always smaller. Thus, we end up with
\[ \begin{aligned} \Phi(z) = -2\pi G \rho \frac{R}{z} \epsilon [R + z - (R - z)] \\ = -4\pi G \rho \epsilon R \end{aligned} \]
Importantly, this only depends on the size of the shell and other constants - the position \( r \) doesn't appear at all! So the potential inside of a spherical shell is constant! To get it in a more familiar form, we recognize that the mass of the spherical shell is
\[ \begin{aligned} M = \int dV' \rho = \int_0^{2\pi} d\phi' \int_0^\pi d\theta' \sin \theta \int_{R-\epsilon}^R dr' r'^2 \\ = 4\pi \rho \frac{1}{3} \left. r'^3 \right|_{R-\epsilon}^R \\ = \frac{4}{3} \rho \pi \left[ R^3 - (R^3 - 3R^2 \epsilon + ...) \right] \\ = 4\pi \rho R^2 \epsilon \end{aligned} \]
so we end up with simply
\[ \begin{aligned} \Phi(r) = -\frac{GM}{R}. \end{aligned} \]
This applies to a hollow sphere with finite width as well, since we can write that potential as an integral over a bunch of spherical shells, all of which will contribute constants that don't depend on the position \( r \) inside the sphere. So inside of a sphere, there is no gravitational force at all!
These surprisingly simple results are actually consequences of some powerful math at work, which we'll explore next.