We've emphasized that the potential tends to be easier to work with than trying to calculate \( \vec{g} \) directly. However, one good reason to use \( \vec{g} \) in certain cases is to invoke some very powerful results from vector calculus. We already mentioned Stokes' theorem briefly in our discussion of curl and conservative forces. Now I'll borrow another result, again without proof, known as Gauss's law:
\[ \begin{aligned} \oint_{\partial V} \vec{g} \cdot d\vec{A} = -4\pi G \int_V \rho(\vec{r}) dV = -4\pi G M_{\rm enc}. \end{aligned} \]
Let's unpack the dense notation here, a lot of which looks very similar to Stokes's theorem. Here \( V \) denotes some volume in three-dimensional space, and \( \partial V \) is the boundary of this volume, which must be a closed surface (in the same way that the boundary \( \partial A \) of a surface is a closed loop); the ring on the integral reminds us of this. We know what everything else is, except for \( M_{\rm enc} \): this is the "enclosed mass", i.e. the total of all the mass contained in the region \( V \).
Where does this result come from? To understand that, we need to introduce our last vector derivative, the divergence, which we get as the dot product of the gradient with another vector. In Cartesian coordinates, we would have
\[ \begin{aligned} \vec{\nabla} \cdot \vec{g} = \frac{\partial g_x}{\partial x} + \frac{\partial g_y}{\partial y} + \frac{\partial g_z}{\partial z} \end{aligned} \]
and the equivalents in cylindrical or spherical are more complicated - refer to the back of Taylor. Gauss's law is actually a special case of a more general vector calculus result known as the divergence theorem, stated without proof: for any vector field \( \vec{b}(\vec{r}) \), the divergence theorem states that
\[ \begin{aligned} \oint_{\partial V} \vec{b}(\vec{r}) \cdot d\vec{A} = \int_V (\vec{\nabla} \cdot \vec{b}(\vec{r})) dV \end{aligned} \]
This matches on to Gauss's law if we make the identification
\[ \begin{aligned} \vec{\nabla} \cdot \vec{g} = -4\pi G \rho(\vec{r}). \end{aligned} \]
This equation is sometimes also called Gauss's law, because one version implies the other one thanks to the divergence theorem. This last equation is also interesting, because we can view it as a differential equation that can be solved for \( \vec{g} \) given \( \rho(\vec{r}) \) - yet another way to obtain the gravitational vector field!
Actually, there's one more simplification we can make here. Remember that the gravitational field is related to the potential as \( \vec{g} = -\vec{\nabla} \Phi \). If we plug this in, we find the equation
\[ \begin{aligned} \nabla^2 \Phi(\vec{r}) = 4\pi G \rho(\vec{r}), \end{aligned} \]
where \( \nabla^2 \) is another new operator called the Laplacian, which is basically the dot product of the gradient \( \vec{\nabla} \) with itself. In Cartesian coordinates,
\[ \begin{aligned} \nabla^2 \Phi = \frac{\partial^2 \Phi}{\partial x^2} + \frac{\partial^2 \Phi}{\partial y^2} + \frac{\partial^2 \Phi}{\partial z^2}. \end{aligned} \]
This differential equation relating \( \Phi \) directly to \( \rho \) is known as Poisson's equation. For some applications, it's the most convenient way to solve for the gravitational field, since we don't have to worry about vectors at all: we get the scalar potential from the scalar density. In particular, Poisson's equation is often a useful way to solve numerically for the potential due to a complicated source density.
We won't use the differential versions of these equations in practice this semester, but they are very useful for more than just numerical solutions: you'll probably see a lot of them when you take electricity and magnetism. But I wanted to explain in a bit more detail where Gauss's law comes from.
Having covered the math, I should say a little bit more about the physical interpretation of Gauss's law. The quantity on the left-hand side, \( \oint_{\partial V} \vec{g} \cdot d\vec{A} \), is known as the gravitational flux through the surface \( \partial V \). There are some hand-waving arguments people sometimes like to make about "counting field lines" to think about flux, but obviously this is a little inaccurate since the strength \( |\vec{g}| \) of the field matters and not just the geometry. Still, a physical way to state Gauss's law is: "for a surface with no enclosed mass, the net gravitational flux through the surface is zero."
Example: gravity far from an arbitrary source
Now let's see the practical use of the integral form of Gauss's law that we wrote down above. I'll use it to prove a very general result that was hinted at by our solutions above: for any massive object of size \( R \), the gravitational field at distances \( r \gg R \) will be exactly the field of a point mass and nothing more. Let's draw a spherical surface of size \( r \gg R \) around our arbitrary object of mass \( M \):
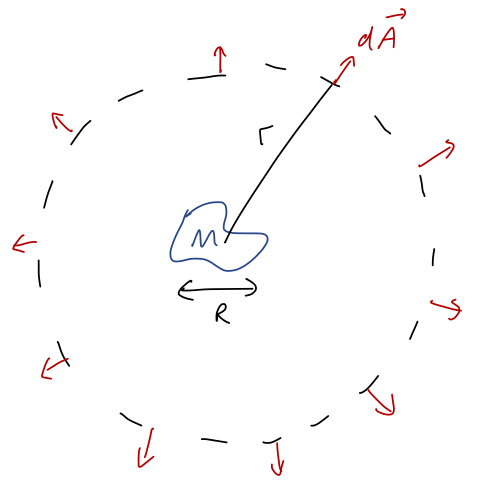
The spherical surface we've chosen here is known as a Gaussian surface - it defines the vector \( d\vec{A} \) and is crucial in applying Gauss's law. We always want to choose the Gaussian surface to match the symmetries of our problem. Since we don't know what \( \vec{g}(\vec{r}) \) is yet, our objective is to choose the right simplifications so we can pull \( \vec{g} \) out of the integral on the left-hand side.
Since \( r \) is much larger than \( R \), the volume integral on the right-hand side of Gauss's law always includes the entire object, and we just get the total mass \( M \). So in other words, for any choice of \( r > R \), we have
\[ \begin{aligned} \oint_{\partial V} \vec{g}(\vec{r}) \cdot d\vec{A} = -4\pi G M. \end{aligned} \]
With our choice of a spherical surface as \( \partial V \), the vector \( d\vec{A} \) is always in the \( \hat{r} \) direction. Explicitly in spherical coordinates,
\[ \begin{aligned} \int_0^{2\pi} d\phi \int_0^\pi d\theta (r^2 \sin \theta) \vec{g}(\vec{r}) \cdot \hat{r} = -4\pi G M \end{aligned} \]
Now let's think about the field \( \vec{g}(\vec{r}) \). If our object were perfectly symmetric, like a sphere, then any components not in the radial direction would cancel off as we've seen, and we would have \( \vec{g}(\vec{r}) = g(r) \hat{r} \). On the other hand, what if it wasn't perfectly symmetric? That would mean we have an imperfect cancellation between the field contributions from two bits of mass that are no more than \( R \) apart from each other. But the contribution from two such pieces has to be something like
\[ \begin{aligned} |\Delta g(\vec{r})| \sim \frac{1}{|\vec{r}'_1 - \vec{r}|^2} - \frac{1}{|\vec{r}'_2 - \vec{r}|^2} \\ = \frac{1}{r^2} \left(1 + \frac{2|\vec{r}'_1|}{r} + ... \right) - \frac{1}{r^2} \left(1 + \frac{2|\vec{r}'_2|}{r} + ... \right) \end{aligned} \]
The \( 1/r^2 \) parts cancel off nicely, so the leading term is something like \( (|\vec{r}'_1| - |\vec{r}'_2|) / r^3 \). But this can't be any larger than \( R/r^3 \), which is \( R/r \) smaller than the leading \( 1/r^2 \) term. In other words, we know that
\[ \begin{aligned} \vec{g}(\vec{r}) = g(r) \hat{r} + \mathcal{O} \left(\frac{R}{r} \right) \end{aligned} \]
even if our object isn't spherically symmetric. If we only keep the leading term, then the integral simplifies drastically:
\[ \begin{aligned} -4\pi G M = \int_0^{2\pi} d\phi \int_0^\pi d\theta \sin \theta r^2 g(r) = 4\pi r^2 g(r) \end{aligned} \]
and since there's no \( r \)-integral, we just have
\[ \begin{aligned} g(r) = -\frac{GM}{r^2} \end{aligned} \]
up to corrections of order \( R/r \), as I assumed.
This is a nice confirmation of the arguments I made above, that everything looks like a point mass if you're far enough away! It's also a simple example of how we use Gauss's law in practice: it's most useful if some symmetry principle lets us identify the direction of \( g(r) \) so that we can actually do the integral on the left-hand side. If we try to keep even the leading \( R/r \) correction, we'll have to find another way to get the answer, because it will have some dependence on the angle \( \theta \) in addition to the distance \( r \).
Example: the hollow sphere again
Let's revisit our calculations for the case of a thin spherical shell of radius \( R \) and total mass \( M \). We'll begin by working outside the sphere, so \( r > R \). We take a Gaussian spherical surface at \( r \) to match our spherical source:
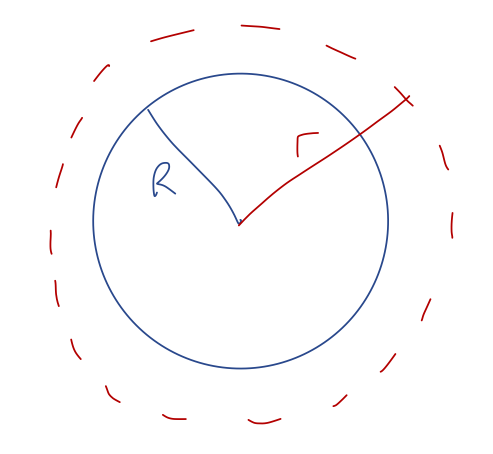
As we've already argued, symmetry tells us immediately that \( \vec{g}(\vec{r}) = g(r) \hat{r} \) in the case of a spherical source. Since \( d\vec{A} \) is also in the \( \hat{r} \) direction for a spherical surface, we have \( \vec{g} \cdot d\vec{A} = g(r) \), which we can pull out of the integral as we saw above. Thus,
\[ \begin{aligned} \oint_{\partial V} \vec{g} \cdot d\vec{A} = -4\pi G \int_V \rho(\vec{r}) dV \end{aligned} \]
becomes
\[ \begin{aligned} 4\pi g(r) r^2 = -4\pi G M \Rightarrow g(r) = -\frac{GM}{r^2}. \end{aligned} \]
This was way easier to find using Gauss's law than the direct calculation we did! What about inside the spherical shell? For \( r < R \), we again take a spherical surface:
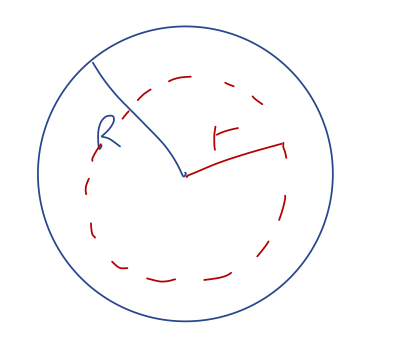
The entire calculation is the same as outside the sphere, except that now \( M_{\rm enc} \) is always zero - correspondingly, we simply have
\[ \begin{aligned} g(r) = 0 \end{aligned} \]
for \( r < R \). This again matches the result we found the hard way before - constant potential, which gives zero \( \vec{g} \) field when we take the gradient.
Clicker Question
Consider a finite disk of radius \( R \) with uniform area mass density \( \sigma \). Suppose we draw a cylindrical Gaussian surface around the disk. Can we use the integral form of Gauss's law to find the gravitational field along the \( z \)-axis?
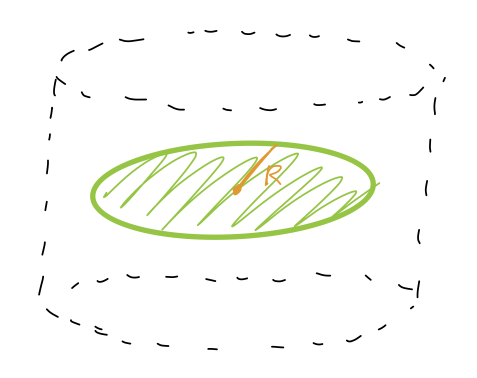
A. Yes; and it will be easier than the direct calculation we did already.
B. Yes; but it's not easier - better to just find the potential.
C. No; Gauss's law applies, but it isn't useful to compute \( \vec{g} \).
D. No; Gauss's law does not apply in this case.
Answer: C
To solve this one, let's start by staring at Gauss's law:
\[ \begin{aligned} \oint_{\partial V} \vec{g} \cdot d\vec{A} = -4\pi G \int_V \rho(\vec{r}) dV \end{aligned} \]
On the right-hand side, we'll just end up with the total mass of the disk for the given Gaussian surface since it encloses the whole thing. So the answer will depend on the left-hand side. In the examples above, we found ways to simplify the left-hand side based on symmetry arguments. Unfortunately, there is no way to do that here! Although the cylindrical surface certainly shares some symmetry properties with the finite disk, it should be clear that the \( \vec{g} \)-field is not uniform across the surface; for example, near the "corners" between the sides and the top or bottom, the field will be pointing diagonally and not perpendicular to \( d\vec{A} \). So the answer definitely isn't A.
To distinguish between B and C, we have to answer whether it's in principle possible to use Gauss's law here. The answer is that it isn't! The problem is that the integral on the left above gives us the total flux through the Gaussian surface - it's an integral over the entire \( \vec{g} \)-field at once. This one number is not enough information to find a specific \( \vec{g} \)-field; there will be an infinite number of possible \( \vec{g} \)-fields that can give the right answer for the flux. So the answer can't be B
On the other hand, the answer isn't D either - if we use another method to solve for \( \vec{g} \) (like the differential form, Poisson's equation) then we expect our answer to satisfy Gauss's law at the end, and we could even use that integral as a check on our solution.