Effective theory; dark matter

Comparison: gravity vs. electric force

You should recognize a lot of similarities between how we're dealing with the gravitational force and how you've seen the electric force treated before. Here's a quick list of equivalences between gravity and electric force:

Gravity vs. electric:

and of course Gauss's law: for gravity we have

\[ \begin{aligned} \oint_{\partial V} \vec{g} \cdot d\vec{A}' = -4\pi G \int_V \rho(\vec{r}') dV' = -4\pi G M_{\rm enc}. \end{aligned} \]

while the electric version reads

\[ \begin{aligned} \oint_{\partial V} \vec{E} \cdot d\vec{A}' = +4\pi k Q_{\rm enc}. \end{aligned} \]

Notice how everything is almost completely identical! The main differences are a different constant (\( G \) vs. \( k \)), a different "charge" (\( m \) and \( M \) vs. \( q \) and \( Q \)), and the minus sign - reflecting the fact that like charges repel in electromagnetism, but they attract for gravity.

A lot of the tools and techniques we're talking about now will transfer more or less directly to electromagnetism; for example, calculating the electric potential \( V(\vec{r}) \) from an extended charged object.

Selected modern topics in gravity

One of the more exciting things about teaching gravitation is that we now have the tools to make contact with some really important and cutting-edge ideas in physics! I'll give you a taste of two such topics: effective theories, and dark matter.

Effective theory and gravity at the Earth's surface

As we've just seen, to the extent that the Earth is a sphere, we know that its gravitational field on the surface and above is

\[ \begin{aligned} \vec{g}(r) = -\frac{GM}{r^2} \hat{r}. \end{aligned} \]

However, this is not the form you use in the lab! For experiments on the Earth's surface, we replace this with the constant acceleration \( g \). In fact, we can derive this by expanding our more general result in the limit that we're pretty close to the Earth's surface.

Let \( R_E \) be the radius of the Earth, \( M_E \) its mass, and suppose that we conduct an experiment at a distance \( z \) above that radius. Then we have

\[ \begin{aligned} \vec{g}(z) = -\frac{GM_E}{(R_E+z)^2} \hat{z} = -g(z) \hat{z} \end{aligned} \]

where I've replaced \( \hat{r} \) with \( \hat{z} \), because if we're on the surface of a sphere, "up" is the same as the outwards radial direction. Now, if we assume that we're relatively close to the surface so \( z \ll R_E \), then a series expansion makes sense:

\[ \begin{aligned} g(z) = \frac{GM_E}{R_E^2 (1 + (z/R_E))^2 } = \frac{GM_E}{R_E^2} \left[ 1 - \frac{2z}{R_E} + \frac{3z^2}{R_E^2} + ... \right] \end{aligned} \]

We see that indeed, so long as \( z \) is very small compared to \( R_E \), then \( g(z) \approx g \), a constant acceleration. We can also see now where \( g \) comes from in terms of other constants; if we measure \( g \approx 9.8 {\rm m}/{\rm s}^2 \), and we also know \( G = 6.67 \times 10^{-11} {\rm m}^3 / {\rm kg} / {\rm s}^2 \) and \( R_E \approx 6400 \) km \( = 6.4 \times 10^6 \) m, then we can find the mass of the Earth:

\[ \begin{aligned} M_E = \frac{gR_E^2}{G} \approx 6 \times 10^{24}\ {\rm kg}. \end{aligned} \]

This is, essentially, the only way we have to measure \( M_E \); the composition of the Earth is complicated and not well-understood beyond the upper layers that we can look at directly, so it's hard to estimate using density times volume.

Our series expansion buys us a lot more than just estimating \( g \)! In particular, we have a specific prediction that if we change \( z \) by enough, we'll be sensitive to a correction term linear in \( z \)

\[ \begin{aligned} g(z) \approx g \left(1 - \frac{2z}{R_E} + ... \right) \end{aligned} \]

Boulder is about 1.6km above sea level, so in this formula, we would predict that \( g \) is smaller by about 0.05% due to our increased height. This is a very small difference, but not so small that it can't be measured! (Although there are other effects of similar size, including centrifugal force due to the fact that the Earth is spinning.)

Now we come to the big idea here, which is the idea of effective theory. This is something which is rarely taught in undergraduate physics, but I believe it's one of the most important ideas in physics - and it's lurking in a lot of what you are taught, even if we don't acknowledge it by name.

My definition of an effective theory is that it is a physical theory which is agnostic about the true underlying physical model, on the basis of identifying a scale separation. If we are interested in some system of size \( r \), then any physics relevant at much longer scales \( L \gg r \) is "separated". So is any physics relevant at much shorter scales, \( \ell \ll r \).

Going back to our example for \( g(z) \), we could also ask about the influence of the Sun's gravity on an object on the Earth's surface; this would depend on the Earth-Sun distance, \( R_{ES} = 1.48 \times 10^{11} \) m. Or maybe we're worried about the quantum theory of gravity, and want to know the effect of corrections that occur at very short distances (our best modern estimate of the length scale at which this would matter is the Planck length, \( \ell_P = 1.6 \times 10^{-35} \) m.) Scale separation tells us that we can series expand such contributions in ratio to the scale \( z \) at which we're experimenting:

\[ \begin{aligned} g(z) \approx g \left( 1 - \frac{2z}{R_E} + ... \right) + C_1 \frac{z}{R_{ES}} + C_2 \frac{\ell_P}{z} + ... \end{aligned} \]

and although we can keep these terms in our expansion, as long as the numerical coefficients \( C_1, C2 \) aren't incredibly, surprisingly large, the ratios \( z/R{ES} \) and \( \ell_P/z \) are so incredibly small that we can always ignore such effects. So we can see the power of scale separation: large enough separation allows us to completely neglect other scales, because even their leading contribution in a series expansion would be tiny!

This validates the effective theory framework of ignoring any physical effects that are sufficiently well-separated, although it's very important to note that this depends on \( z \), the experimental scale. An effective theory doesn't claim to be the right and final answer: it's only "effective" for a certain well-defined set of experiments. If our \( z \) approaches any one of these other scales, then the series expansion relying on scale separation will break down, and we'll have to include the new physics at that scale to get the right answer.

A couple of slightly technical points I should make on the last equation I wrote. You might wonder why I can assume the series expansion for something like the Earth-Sun distance starts at \( z/R_{ES} \). Why can't there be an \( R_{ES} / z \) term, for example? That wouldn't make any physical sense, basically - it would imply that there's a large effect from the Earth-Sun distance in the limit that \( R_{ES} \) goes to infinity. We can't have a \( \ell_P/z \) term for a similar reason - it makes no sense as \( \ell_P \) goes away (goes to zero.)

Now, this isn't a guarantee that there's no possible effect from the other physical scales present. In this example, if \( R_{ES} \) was significantly smaller, there might be terms like \( R_{ES} / R_E \) which aren't necessarily completely negligible. But this doesn't depend on \( z \) - \( z \) is a scale that we define as part of the effective theory. So such a correction could change the leading-order constant term \( g \), or the coefficients of other terms, but it can't alter the form of the \( z \)-dependence, as long as we still have scale separation between \( z \) and \( R_{ES} \).

This leads to a second way to think about effective theory. Even if we didn't know the full Newtonian theory of gravity, experimenting with gravity at different heights above the Earth's surface would still tell us that there is some dependence on the height. We could have instead built a top-down effective theory, where we don't know the fundamental theory at all, but we use experiment and symmetry to formulate a theory. From experiments on the Earth, it's easy to discern that (1) \( g \) is almost a constant downwards acceleration, and (2) there is some dependence on the height \( z \). Based on those two observations, we can write a very general Taylor series in \( z \) over an unknown length scale \( L \):

\[ \begin{aligned} g(z) = g + g_1 \frac{z}{L} + g_2 \frac{z^2}{L^2} + ... \end{aligned} \]

Now we go out and do experiments to measure the acceleration due to gravity at lots of different heights, and then we find the values \( g_0, g_1, g_2 \) that describe our data. Once we've done that exercise, we now have a working theory of gravity that we can use to make predictions - without knowing anything about the more fundamental theory!

Of course, this will break down at some point; when \( z \) approaches the unknown length scale \( L \), the expansion won't converge and our predictions will fail. But this is actually a feature of top-down effective theories: they let you know when they begin to break! And by doing enough experiments to infer the \( z \)-values where this theory begins to fail, we can actually discover what the value of \( L \) is, which can be a big hint as to what the more fundamental theory is. (In this case, we know the right answer already: \( L \) is \( R_E \), the Earth's radius.)

There is another way that our effective theory can fail: if we neglect to include some physical effect which is actually important. In this case, we have done just that: the Earth is not perfectly spherical, and its density is also not uniform. So if we just keep our height above sea level \( z \) fixed and try to measure \( g(z) \), we will find different results depending on where we are on the Earth! After doing some experiments, we would need to revise our effective theory to \( g(x,y,z) \), accounting for the additional variation with our position on the Earth's surface. This is an experimental question, and in fact experiments such as NASA's GRACE satellite have done just that:

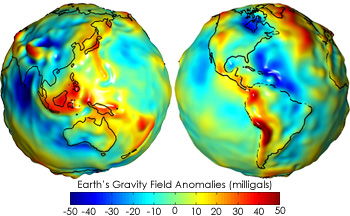
(image from https://earthobservatory.nasa.gov/features/GRACE/page3.php.) The measurement shown is the gravity "anomaly", which is the deviation from the prediction for a smooth, uniform Earth. The unit of "milligal" is a unit of acceleration named after Galileo; one gal is equal to \( 0.01 \) m/s\( ^2 \), which works out to about 1/1000 the size of \( g \), so a milligal is 1/10^6 times \( g \). Our estimated correction to \( g \) in Boulder of 0.05% of \( g \) works out to 500 milligals, so height is the dominant effect (and has clearly been subtracted to produce the shown anomaly map.)

Effective theory is a seemingly simple idea: basically an application of series expansion once again. But again, this is a really important idea in physics! Whenever we write down Newton's laws, we're also ignoring long-distance effects from things like the Sun's gravitational field, and we're ignoring quantum effects that will show up around atomic distance scales. So all of Newtonian physics is in fact an effective theory!

In fact, all of the "fundamental" forces are effective theories too, as far as we know. A famous example is gravity itself; if we try to calculate using the theory of gravity on scales where quantum mechanics is also important, then we find that the resulting effective theory diverges badly if we even ask theoretical questions about distances close to \( \ell_P \), the Planck length I mentioned above. This is such an enormously short distance scale that we have no experiments that can possibly probe it, so far - but effective theory gives us a tantalizing hint that gravity has to change somehow if we can start to look at those really short distances.

Dark matter

The story of dark matter begins with a really simple physics question: how do we know the mass of the Sun \( M_{\odot} \)? I mentioned before that for the Earth, there's only one reliable measurement of its mass, which is using the force of gravity exerted by the Earth. We can do the same for the Sun, by looking at the Earth's orbit.

The force on the Sun due to the Earth is

\[ \begin{aligned} \vec{F}_g = -\frac{GM_{\odot} M_E}{R_{ES}^2} \end{aligned} \]

Now, the orbit of the Earth isn't perfectly circular, but it's pretty close; if we assume that it is circular, then this is also a centripetal force:

\[ \begin{aligned} \vec{F}_g = \vec{F}_c \Rightarrow \frac{GM_{\odot} M_E}{R_{ES}^2} = \frac{M_E v_E^2}{R_{ES}} \end{aligned} \]

or solving for the mass of the Sun,

\[ \begin{aligned} M_{\odot} = \frac{v_E^2 R_{ES}}{G}. \end{aligned} \]

Finding the speed of the Earth's orbit is easy: we know it completes a full orbit in 1 year, or 365.25 days. A full orbit is a change in angle of \( 2\pi \), so the Earth's angular speed is

\[ \begin{aligned} \omega_E = \frac{2\pi}{365.25\ {\rm days}} \approx 2.0 \times 10^{-7} / s. \end{aligned} \]

Since \( v_E = \omegaE R{ES} \), we now know \( vE \) in terms of \( R{ES} \). Determining the latter is actually tricky, although there are estimates dating back as much as 2300 years ago; I won't go into details, but it involves geometric arguments with the Sun, Earth, and another astronomical body making a triangle. The advent of radar ranging to other planets can be combined with modern versions of these geometric calculations to yield a fairly accurate result, which I already quoted above: \( R_{ES} \approx 1.48 \times 10^{11} \) m.

Putting things together, we find

\[ \begin{aligned} M_{\odot} = \frac{\omega_E^2 R_{ES}^3}{G} = 1.9 \times 10^{30}\ {\rm kg}. \end{aligned} \]

For the Sun, we actually have a second way to estimate its mass: based on its size and density. Again using geometry, the radius of the Sun itself can be determined to be \( R_{\odot} = 7.0 \times 10^5 \) km. Thus, the mass will be related to the density as

\[ \begin{aligned} M_{\odot} = \rho_{\odot} V_{\odot} = \frac{4}{3} \pi R_{\odot}^3 \rho_{\odot}. \end{aligned} \]

We can estimate the density of the Sun because we know what it's made of: primarily hydrogen and helium, heated into a superhot plasma. Now, this is definitely not a simple exercise: the temperature will have significant effects on the density, and so will the additional pressure generated by the huge gravitational pull of the Sun. But we have fairly complete models of the Sun's interior, and it's certainly possible to do the calculation carefully and get an estimate - see here for a taste of how such models work - of about 1400 kg/\( {\rm m}^3 \). This once again gives a result of \( M_{\odot} \sim 2 \times 10^{30} \) kg.

This is a nice consistency check between our model of gravity and our model of the Sun. It also suggests a similar approach to a much more ambitious question: how much mass is in a galaxy like the Milky Way? The second method for weighing a galaxy is straightforward: you estimate how many stars there are, multiply by the mass of an average star (very roughly the mass of the Sun, but there are detailed models of stellar populations that can improve this!), and that gives you one version of \( M_{\rm galaxy} \).

The gravitational way of estimating a galaxy's mass turns out to be a bit more involved. But we have a lot of extra information: since we can infer the motion of all of the visible stars in a galaxy, we can see "inside" the galaxy to probe its complete gravity field instead of having to rely only on objects well outside the galaxy, as we did for the Earth-Sun case.

Let's restrict our attention to a certain fairly common kind of galaxy known as an elliptical galaxy, which can be nearly spherical - in fact, let's assume it is spherical for the sake of our calculation. (I'll comment on this assumption later.)

To find the gravitational field, we need to consider another variant of the sphere problem: finding the field inside of a solid sphere. We can set this up simply using Gauss's law. Let's take a sphere of radius \( R \) and consider \( r < R \) as shown:

Applying Gauss's law using the spherical surface at distance \( r \), we have \( d\vec{A} = r^2 \sin \theta \hat{r} \) and \( \vec{g} = g(r) \hat{r} \), so

\[ \begin{aligned} \oint_{\partial V} \vec{g} \cdot d\vec{A} = -4\pi G \int_V \rho(\vec{r}) dV \\ 4\pi r^2 g(r) = -4\pi G \int_0^{2\pi} d\phi' \int_0^\pi d\theta' \int_0^r dr'\ \rho(\vec{r}') r'^2 \sin \theta' \end{aligned} \]

Clicker Question

Ignoring any numerical constants, how does the gravitational field \( g(r) \) scale with \( r \)?

A. \( g(r) \sim 1/r^2 \)

B. \( g(r) \sim 1/r \)

C. \( g(r) \sim R \), i.e. constant in \( r \)

D. \( g(r) \sim r \)

E. \( g(r) \sim r^2 \)

Answer: D

To answer this, I'll just do the full integral including the constants. The key is that \( \rho(r') = \rho \) is a constant, so we can pull it out of the integral completely and end up with the volume of the inner sphere:

\[ \begin{aligned} 4\pi r^2 g(r) = -4\pi G \rho \left( \frac{4}{3} \pi r^3 \right) \end{aligned} \]

or rearranging,

\[ \begin{aligned} g(r) = -\frac{4}{3} \pi G \rho r. \end{aligned} \]

So the strength of the gravitational field actually increases with distance! We can't observe the gravity field directly, just the motion of the stars, so we have one more step, to relate this to the speed. The main dynamics of a galaxy is not that different from our solar system: the stars follow orbits around the galactic center of mass. If we make the assumption of an approximately circular orbit, then the force of gravity must be equal to the centripetal force,

\[ \begin{aligned} |\vec{F}_g| = |\vec{F}_c| \\ m|\vec{g}(r)| = \frac{mv^2}{r} \\ \frac{4}{3} \pi G \rho r = \frac{v^2}{r} \\ v = \sqrt{\frac{4\pi G \rho}{3}} r. \end{aligned} \]

We can measure \( v \) and \( r \), and then extract the density \( \rho \) from this equation to find the galaxy mass. Of course, this is only true inside the sphere, or equivalently in the middle of the galaxy where the density really is more or less constant. But if we look at stars close to the edge of the galaxy, we can treat them as being just outside a sphere, and we have our previous result

\[ \begin{aligned} g(a) = -\frac{GM_{\rm enc}}{r^2} \end{aligned} \]

for \( r > R \). Relating to the speed in the same way as before, we have

\[ \begin{aligned} \frac{GM_{\rm enc}}{r^2} = \frac{v^2}{r} \\ v = \sqrt{\frac{GM_{\rm enc}}{r}}. \end{aligned} \]

So if we can get good observations of stars at the edge of a galaxy, we can just measure their speeds directly to determine the mass. Overall, if we look at all of the stars, if the density is constant out to the edge of the visible galaxy at \( R \), we expect the profile of speed vs. distance to look like this:

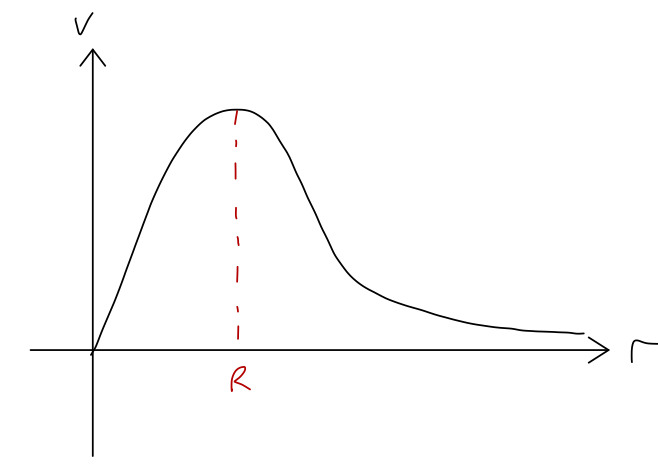
(Our prediction isn't this smooth near \( R \), but a smooth function is more realistic, due to measurement error and the fact that the density of a galaxy isn't really uniform.) So far, so good. But what do we see if we actually do this experiment? Here is a plot of \( v \) vs. \( r \) for the galaxy NGC 3198: this is a spiral galaxy and not an elliptical, so I'm cheating a little; spirals seem to be easier to make this sort of observation of the full rotation curve in, probably because we get an unobstructed view of stars all the way to the center.

(from https://jila.colorado.edu/~ajsh/astr1200_18/dm.html, and originally https://ui.adsabs.harvard.edu/abs/1985ApJ...295..305V/abstract.)

The "disk" line shows the expected dependence; the data points show the observed results. You can see from the disk line that in this model, \( R \) for the galaxy is about 6 kpc (kilo-parsecs, a parsec is short for "parallax arcsecond" and is one of those somewhat arcane astronomy units; a parsec is about 3.3 light-years.) For small \( r \) the data agree well with the disk model, with speed increasing with distance, but then instead of the expected turnover, the velocity just becomes constant out to well beyond where the visible edge of the dense part of the galaxy is found!

One possibility is that we've neglected something: there is another force that we don't know about, or our model of gravity is just wrong. This is still a possibility, although the preponderance of evidence is strongly in favor of the second option: dark matter. That is to say, what we have wrong isn't the force law, but the density function: there must be some additional source of gravity that extends out beyond where the visible stars end. Quite far beyond, in fact; for most galaxies, a full explanation requires an enormous dark matter "halo" surrounding the visible galaxy:

This has to be "dark" because it doesn't emit or absorb light at all, or at best it does so very weakly; astronomical observations across the spectrum of light show nothing at all where the gravitational mass should be plentiful. This also brings me back to the comment about spherical galaxies: even for a spiral galaxy, the dark matter halo itself is still spherical (and much larger than the galaxy itself!), so our calculation still applies.

We can even guess what the density of the missing dark matter is using what we've derived so far: as you can see from the plot, the contribution to the speed from the halo goes roughly as \( \sqrt{r} \). Working backwards, this requires a constant gravitational field, which in turn means that for the dark matter halo,

\[ \begin{aligned} \rho(r) \propto \frac{1}{r}. \end{aligned} \]

Of course, this is only one galaxy; there are other examples where \( v(r) \) becomes constant (which would require \( \rho(r) \propto 1/r^2 \)) or begins to drop at very large distances. A commonly adopted model which works well for a large number of galaxies is the Navarro-Frenk-White profile, or NFW profile for short:

\[ \begin{aligned} \rho_{\rm NFW}(r) = \frac{\rho_0}{(r/a)(1 + r^2/a^2)} \end{aligned} \]

introducing a second length scale \( a \), the "scale radius". This model can be argued as a simple but general parametrization of the behavior of so-called "cold and collisionless" dark matter - which can be tested using numerical simulations consisting of N masses only interacting through gravity.

Since it's an active topic of research, I should say a little more about what we do know about dark matter. So far, the answer is "not very much"; experimental searches that attempt to capture the passing of a dark matter particle through an Earth-based detector have so far yielded nothing, except strong confirmation that it is indeed "dark" - any other interaction it has with ordinary matter must be very weak indeed.

However, we have a large amount of evidence for the gravitational effects of dark matter. In addition to observations of galactic structure (for which there are many examples):

The story is not completely settled, of course; maybe a modification of gravity can account for all of the above, although since very different distances scales are involved it is quite difficult to formulate such a theory. The more likely explanation is that dark matter exists, and the hunt is on to discover what it is!