Concept: Phase space
In exploring the behavior of the Lotka-Volterra equations, we relied heavily on numerical study of how solutions evolve in the plane of the two variables \( R \) and \( F \), hiding the dependence on the independent variable \( t \). The space of \( R \) and \( F \) is known as the state space, and we can make powerful observations such as the fact that no two paths will cross.
Can we apply these geometric ideas to a physical system that has non-linear dynamics, like, say, the simple pendulum?
\[ \begin{aligned} \ddot{\theta} = -\frac{g}{L} \sin \theta. \end{aligned} \]
Our first problem is that this is now a second-order differential equation; we could try to plot \( \ddot{\theta} \) vs. \( \theta \), but that doesn't give us enough information to tell how the system evolves, since it depends on \( \dot{\theta} \) at that instant too.
Now what? Let's refresh our memory about exactly where the equation of motion comes from. At the beginning of the semester, we introduced Lagrangian mechanics as a radical new way of looking at (and solving for the motion of) mechanical systems.
One of the central concepts that we introduced was the idea of a generalized coordinate, \( q_i \). The \( q_i \) are a set of functions of the spatial coordinates of all of the objects in our system, plus time:
\[ \begin{aligned} q_i = q_i(\vec{r}_1, \vec{r}_2, ..., \vec{r}_N, t). \end{aligned} \]
With three spatial dimensions, and with \( m \) constraints on the system, we need \( 3N - m \) independent generalized coordinates to describe the position of the system.
With the Lagrangian and the generalized coordinates in hand, the motion of the system is described by the Euler-Lagrange equations,
\[ \begin{aligned} \frac{\partial \mathcal{L}}{\partial q_i} = \frac{d}{dt} \left( \frac{\partial \mathcal{L}}{\partial \dot{q_i}} \right). \end{aligned} \]
At the very end of our discussion of Lagrangian mechanics, we came to the idea of conserved quantities, that is to say, quantities which don't change as the system evolves (total energy \( E \) is the most familiar example you know.) From studying the Euler-Lagrange equations, we found in particular that if the Lagrangian is independent of any of the \( q_i \), so \( \partial \mathcal{L} / \partial q_i = 0 \), then
\[ \begin{aligned} \frac{\partial \mathcal{L}}{\partial q_i} = 0 \Rightarrow \frac{\partial \mathcal{L}}{\partial \dot{q}_i} \equiv p_i = \textrm{const}. \end{aligned} \]
The \( p_i \) is the generalized momentum associated with coordinate \( q_i \); for a Cartesian coordinate like \( x \), it's just the linear momentum \( p_x \).
Now, notice that even if \( \partial \mathcal{L} / \partial q_i \neq 0 \), we can still write the equation of motion in terms of the momentum, except now it's not constant anymore:
\[ \begin{aligned} \frac{\partial \mathcal{L}}{\partial q_i} = \dot{p_i}. \end{aligned} \]
This is a first-order differential equation for the momentum, \( p_i \)! Let's go back to the pendulum example: the Lagrangian for the simple pendulum is
\[ \begin{aligned} \mathcal{L} = \frac{1}{2} m L^2 \dot{\theta}^2 + mgL \cos \theta \end{aligned} \]
so the generalized momentum is
\[ \begin{aligned} p_\theta = mL^2 \dot{\theta}, \end{aligned} \]
and its differential equation is
\[ \begin{aligned} \dot{p}_\theta = -mgL \sin \theta. \end{aligned} \]
We have reduced one second-order differential equation to a pair of first-order equations (in general, \( N \) second-order diff eqs give us \( 2N \) first-order ones.) The space defined by the combination of generalized coordinates \( q_i \) and their associated generalized momenta \( p_i \) is known as phase space.
Now we can plot the gradient in the space of \( (\theta, p_\theta) \), just as we did for the Lotka-Volterra equations! Let's set \( m = L = g = 1 \) and just focus on the numerics.
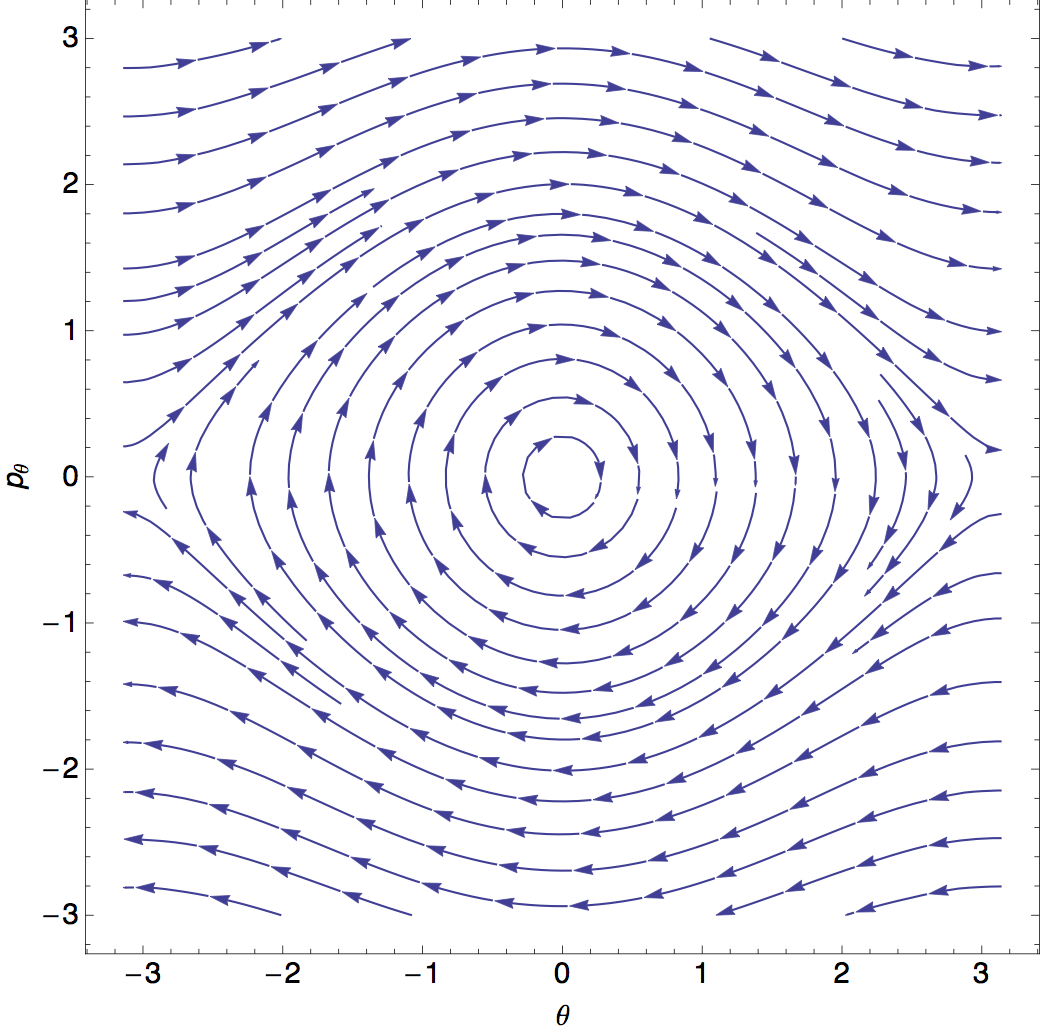
This is a (graphical) solution to the pendulum, for arbitrary angles, no small-angle approximation needed! (Such a sketch in phase space is known as a phase portrait.) For small angles, we see circles corresponding to simple harmonic motion: if our small-angle solution is \( \theta(t) \propto \cos(t) \), then \( p_\theta \propto \dot{\theta} \propto \sin(t) \), which is the parametric equation for a circle.
At large \( p_\theta \), meanwhile, we can also easily visualize the motion: up to small fluctuations, \( p_\theta \) remains large and roughly constant through the motion. This corresponds to the pendulum swinging in a circle around the support (remember that \( \theta = -\pi \) and \( \theta = +\pi \) are the same point, so every curve here is still closed!)
There is a single curve separating back-and-forth harmonic motion from the constant spinning motion; it's called the separatrix, and it's the phase-space path that is still a closed loop, but just barely touches \( \theta = -\pi \) and \( \theta = \pi \). The motion of the pendulum along the separatrix is particularly funny; it comes to a (nearly) complete stop in a (nearly) vertical position, then falls back down the other way, and repeats. (Of course, if we have exactly \( \theta = \pi \) and \( p_\theta = 0 \), the pendulum doesn't move at all. This is an unstable equilibrium point.)
This is a lot of progress for one small plot! Using phase space to split our equations of motion into coupled first-order differential equations is a very powerful technique. However, things were particularly simple here, especially the equation \( p_\theta = \partial \mathcal{L} / \partial \theta \). In general, just using that equation won't just lead us to a simple first-order differential equation; the derivative could be some more complicated function of the coordinate derivatives.
But don't give up yet, because there is a way to generally arrive at first-order equations, and that is through the Hamiltonian.
Concept: Hamiltonian mechanics
Way back in our study of Lagrangian mechanics, we defined an object called the Hamiltonian,
\[ \begin{aligned} \mathcal{H} = \sum_i p_i \dot{q}_i - \mathcal{L}, \end{aligned} \]
where \( q_i \) are generalized coordinates and \( p_i \) are their associated generalized momenta,
\[ \begin{aligned} p_i = \frac{\partial \mathcal{L}}{\partial \dot{q}_i}. \end{aligned} \]
We observed at the time that with certain assumptions (no time-dependent coordinates), the Hamiltonian was equal to the total energy - and in any case, it is always a conserved quantity, \( d\mathcal{H} / dt = 0 \), as a consequence of time translation invariance.
Now we're ready to see an application of the Hamiltonian, which is working in phase space. Let's focus for the moment on the case of a single \( q \); generalizing to many coordinates is easy. Then I can drop the sum, and just write
\[ \begin{aligned} \mathcal{H} = p\dot{q} - \mathcal{L}. \end{aligned} \]
Since we want to work in phase space, we should treat \( \dot{q} \) as a function of the phase-space variables:
\[ \begin{aligned} \dot{q} = \dot{q}(q,p). \end{aligned} \]
(Remember, we have an equation defining \( p \) from the derivative \( \partial \mathcal{L} / \partial q \); we can just go back and invert it to get this function, usually.) With this replacement, the full Hamiltonian (and the Lagrangian) can be written as functions of only \( p \) and \( q \):
\[ \begin{aligned} \mathcal{H}(p,q) = p \dot{q}(p,q) - \mathcal{L}(q, \dot{q}(p,q)). \end{aligned} \]
Now let's start taking derivatives, and see if applying the Euler-Lagrange equations of motion will get us anywhere. First,
\[ \begin{aligned} \frac{\partial \mathcal{H}}{\partial q} = p \frac{\partial \dot{q}}{\partial q} - \left[ \frac{\partial \mathcal{L}}{\partial q} + \frac{\partial \mathcal{L}}{\partial \dot{q}} \frac{\partial \dot{q}}{\partial q} \right] \end{aligned} \]
(this is a straightforward application of the chain rule.) But we know already that by definition, \( \partial \mathcal{L} / \partial \dot{q} = p \). So two of the terms cancel, and we just have
\[ \begin{aligned} \frac{\partial \mathcal{H}}{\partial q} = - \frac{\partial \mathcal{L}}{\partial q} \end{aligned} \]
Now, we remember the Euler-Lagrange equation: the right-hand side is the time derivative of \( \partial \mathcal{L} / \partial \dot{q} \), which we recognize once again is just \( p \). Thus,
\[ \begin{aligned} \frac{\partial \mathcal{H}}{\partial q} = -\dot{p}. \end{aligned} \]
The other variable we have lying around is \( p \):
\[ \begin{aligned} \frac{\partial \mathcal{H}}{\partial p} = \dot{q} + p \frac{\partial \dot{q}}{\partial p} - \frac{\partial \mathcal{L}}{\partial \dot{q}} \frac{\partial \dot{q}}{\partial p}. \end{aligned} \]
This time the last two terms cancel, and so we have
\[ \begin{aligned} \frac{\partial \mathcal{H}}{\partial p} = \dot{q}. \end{aligned} \]
This is exactly what we were looking for - a set of coupled, but first-order differential equations of motion! (This might all seem kind of arbitrary and/or miraculous to you just from this derivation. There is, in fact, a general mathematical technique called the Legendre transformation which allows second-order differential equations to be traded for first-order ones by introducing an auxiliary variable like the momentum here. If you've taken a math class in diff-eq, you may have seen the Legendre transform before.)
As I said, the derivation for a larger number of coordinates isn't very difficult. If you do it, you will arrive at Hamilton's equations:
\[ \begin{aligned} \dot{p}_i = -\frac{\partial \mathcal{H}}{\partial q_i} \\ \dot{q}_i = \frac{\partial \mathcal{H}}{\partial p_i}. \end{aligned} \]
Note that if \( \partial \mathcal{H} / \partial q_i = 0 \), then the corresponding momentum \( p_i \) is conserved: \( \dot{p_i} = 0 \).
While we're thinking about time-dependence, we recall that in many situations \( \mathcal{H} = T + U \), but only when the coordinates are all independent of time, i.e. \( \partial q_i / \partial t = 0 \). (Note that this includes coordinates that are eliminated by constraints, if the constraint is time-dependent; you should be careful with such situations.) It's straightforward to show the relations:
\[ \begin{aligned} \frac{d\mathcal{H}}{dt} = \frac{\partial \mathcal{H}}{\partial t} = -\frac{\partial \mathcal{L}}{\partial t}. \end{aligned} \]
which is another way of stating that if the Hamiltonian has no explicit time dependence, i.e. \( \partial \mathcal{H} / \partial t = 0 \), then it is totally conserved, \( d\mathcal{H} / dt = 0 \).
For the pendulum, we made a big deal out of the fact that paths in phase space can't cross, because given all the \( p_i \) and \( q_i \), the derivatives give us a unique direction in phase space in which the system will evolve in an infinitesmal time \( dt \). Note that this is only true if \( \partial \mathcal{H} / \partial t = 0 \); if \( \mathcal{H} \) is changing, then knowing just \( p_i \) and \( q_i \) isn't sufficient to tell us the derivatives. (Hamilton's equations will work just fine whether there's extra time-dependence or not, but making sketches in phase space is much less useful.)
Going beyond the simplest problems, we won't be able to simply draw phase-space diagrams on the board; even for just two independent non-ignorable coordinates, the phase space becomes 4-dimensional (good luck drawing that.) But we can still use the language of geometry in this higher-dimensional space to make some progress. In general, we can combine the coordinates \( q_i \) and momenta \( p_i \) into one large \( 2N \)-component phase-space vector:
\[ \begin{aligned} \vec{z} = (\vec{q}, \vec{p}) = (q_1, ..., q_n, p_1, ..., p_n). \end{aligned} \]
This is sometimes also known as the phase point. Thanks to the Hamiltonian approach, we can write down Hamilton's equations, which give us a single vector-valued differential equation:
\[ \begin{aligned} \dot{\vec{z}} = \vec{h}(\vec{z}). \end{aligned} \]
I've written the function \( \vec{h} \) itself as a vector, to remind us that this isn't just a function of a vector, it's \( 2n \) independent functions coming from Hamilton's equations. (If all of the functions \( \vec{h} \) are linear then we can write it as a matrix, but that's not guaranteed.)
Note also that if \( \partial \mathcal{H} / \partial t \neq 0 \), then we actually have \( \dot{\vec{z}} = \vec{h}(\vec{z}, t) \); this will complicate some of the discussion we're about to have, so I'll assume time-independence for now. Combining \( p \) and \( q \) into a large vector is made possible by the fact that in the Hamiltonian approach, we treat positions and momenta on (nearly) equal footing. This equal treatment enables some other interesting tricks, which I won't go into here (but you'll find such devices as canonical transformations if you go on to study graduate-level classical mechanics.)
Formula: Hamilton's equations
Although the main motivation we had for coming this far was to think in terms of phase space (which will have some further nice, geometric properties which we will come to!), Hamilton's equations also provide us with yet another way to find the motion of a dynamical system. Here's the general procedure, as a checklist:
How to use the Hamiltonian
- Set up the Lagrangian as usual, with some generalized coordinates \( q_i \).
- Find the generalized momenta \( p_i = \partial \mathcal{L} / \partial \dot{q}_i \).
- Solve for \( \dot{q}_i \) in terms of the \( p_i \) and \( q_i \).
- Rewrite \( T \) and \( U \) in terms of \( q_i \) and \( p_i \).
- Find \( \mathcal{H} \), as \( T+U \) if all the \( \partial q_i/\partial t = 0 \) (including constraints!), otherwise as \( \sum_i p_i \dot{q}_i - \mathcal{L} \)
- Apply Hamilton's equations to get the equations of motion:
\[ \begin{aligned} \dot{p}_i = -\frac{\partial \mathcal{H}}{\partial q_i}, \\ \dot{q}_i = \frac{\partial \mathcal{H}}{\partial p_i}. \end{aligned} \]
Once we have the equations of motion, we can look for equilibrium points, make phase-space portraits, solve for \( q_i(t) \) explicitly, etc.
A very common mistake when trying to use Hamilton's equations is putting the minus sign in the wrong place. A quick and easy way to remember is to apply it to the free Hamiltonian: for a particle with one dimension with \( U = 0 \), we have just
\[ \begin{aligned} \mathcal{H}_{\rm free} = T = \frac{p^2}{2m}. \end{aligned} \]
Then the second of Hamilton's equations gives \( \dot{q} = p/m \), which is just the usual definition of linear momentum - with no minus sign!
Typically my examples are separate in this lecture format, but I think we need one simple example here to get a better feeling for how Hamiltonian mechanics works.
Example: the simple harmonic oscillator
We'll take \( x \) as our lone generalized coordinate. We all know how to write this Lagrangian in our sleep:
\[ \begin{aligned} \mathcal{L} = \frac{1}{2} m \dot{x}^2 - \frac{1}{2} kx^2. \end{aligned} \]
The generalized momentum is just the linear momentum, but let's do it the careful way:
\[ \begin{aligned} p_x = \frac{\partial \mathcal{L}}{\partial \dot{x}} = m \dot{x}, \end{aligned} \]
so \( \dot{x} = p_x / m \).
Let's find the Hamiltonian the careful way first. Rewriting the Lagrangian, we have:
\[ \begin{aligned} \mathcal{L} = \frac{p_x^2}{2m} - \frac{1}{2} kx^2. \end{aligned} \]
Applying the general formula for the Hamiltonian gives
\[ \begin{aligned} \mathcal{H} = p_x \dot{x} - \mathcal{L} \\ = p_x \dot{x} - \frac{p_x^2}{2m} + \frac{1}{2} kx^2 \\ = \frac{p_x^2}{2m} + \frac{1}{2} kx^2 \end{aligned} \]
which is of course just \( T + U \), since in this case we have no time-dependent coordinates or constraints.
Now we can take derivatives to get Hamilton's equations:
\[ \begin{aligned} \dot{p_x} = -\frac{\partial \mathcal{H}}{\partial x} = -kx \\ \dot{x} = \frac{\partial \mathcal{H}}{\partial p_x} = \frac{p_x}{m}. \end{aligned} \]
Ironically enough, the easiest way to solve this is just to plug one equation into the other, say by taking the derivative of the \( \dot{x} \) equation:
\[ \begin{aligned} \ddot{x} = \frac{\dot{p_x}}{m} = -\frac{k}{m} x \end{aligned} \]
which should look very familiar by now. We could draw the phase-space plot, but it will be unsurprisingly boring: we know the solution is just a simple harmonic oscillator no matter what \( x \) or \( p_x \) are. Explicitly, the gradient of \( (x, p_x) \) is
\[ \begin{aligned} (\dot{x}, \dot{p}_x) = (p_x/m, -kx) \end{aligned} \]
We can use this numerically, but since we're drawing paths that the system follows through time, we can also use the solution that we already know:
\[ \begin{aligned} x = x_0 \cos(\sqrt{k/m} t - \delta) \\ p_x = m\dot{x} = -mx_0 \sqrt{k/m} \sin (\sqrt{k/m} t - \delta) \end{aligned} \]
This is just the equation for a ellipse, with the polar angle given by the argument of the cosine. We can see this expliclty by noticing that
\[ \begin{aligned} \frac{x^2}{x_0^2} + \frac{p_x^2}{mkx_0^2} = \cos^2 (...) + \sin^2 (...) = 1 \end{aligned} \]
which is the standard equation for an ellipse in the \( x-p_x \) plane; the axes are \( 2x_0 \) and \( 2\sqrt{mk} x_0 \).
Concept: Liouville's theorem
We've focused a lot on individual phase-space trajectories, where we pick some exact starting value for our mechanical system and then just let it evolve. But in the real world, we can never be exactly certain of the state of our system; there will always be some measurement error. Because of this, it's an interesting question to ask not just how a point evolves in phase space, but how a volume will evolve. If we only know that our system's initial state lies within some volume, how accurately can we predict where it will be in the future?
(Incidentally, the idea of phase space volumes is also very useful if we're studying a large collection of particles, like a gas, something which really would occupy a volume in phase space even if we didn't have any measurement uncertainty.)
Let's consider a simple example, that of a particle in freefall, just to see what happens. What is the phase-space trajectory of a single particle in freefall? We know that \( \dot{p_z} = mg \) and \( \dot{z} = -gt \). But we want to plot in terms of \( z = \frac{1}{2} gt^2 \) and \( p_z = mgt \). So, we see that \( z \propto p_z^2 \), which is the equation for a sideways parabola (or a square-root function):
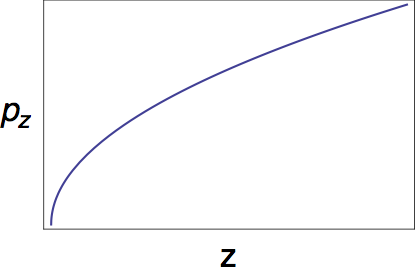
If we change the initial conditions, then the trajectory will start at a different point, but will still be described by a sideways parabola. If we start with an initial region, say a square, its area will be distorted as the points within it evolve in time:
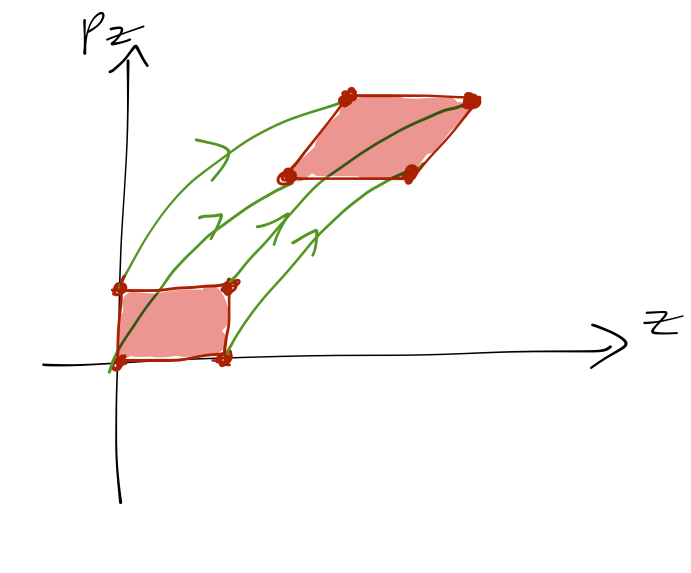
(A region like this might represent some uncertainty in setting or measuring our initial conditions, for example.) Although our initial region of phase space has become distorted by the time evolution of the system, the area of the region is the same before and after! This isn't a coincidence, or unique to simple systems like this, it's a very powerful and general result of Hamiltonian mechanics, known as Liouville's theorem.
Taylor has a derivation of Liouville's theorem involving vector calculus, but it's a somewhat long and involved argument, so I'm going to show you another way to derive it. Once again I'll do the derivation with a single coordinate and single momentum \( (q,p) \); it's very easy to generalize. Suppose we have a really tiny volume of phase space centered around the point \( \vec{z}_0 = (q_0, p_0) \).
\[ \begin{aligned} V = dq dp. \end{aligned} \]
Now we let our tiny volume evolve for an infinitesmal time step, \( dt \). We know that the center point \( \vec{z}_0 \) evolves according to Hamilton's equations, i.e.
\[ \begin{aligned} q_0 \rightarrow q_0 + \dot{q} dt = q_0 + \frac{\partial \mathcal{H}}{\partial p} dt = \tilde{q}_0,\\ p_0 \rightarrow p_0 + \dot{p} dt = p_0 - \frac{\partial \mathcal{H}}{\partial q} dt = \tilde{p}_0. \end{aligned} \]
The small volume evolves in the same way:
\[ \begin{aligned} \tilde{V} = d\tilde{q} d\tilde{p} = (\det J) V \end{aligned} \]
where \( J \) is the Jacobian matrix describing the change of coordinates. This factor is completely familiar as the extra term which appears when we do integrals in spherical or cylindrical coordinates. In general, the Jacobian is a matrix of all the partial derivatives given by our coordinate change: in index notation,
\[ \begin{aligned} J_{ij} = \frac{\partial \tilde{z}_i}{\partial z_j} \end{aligned} \]
or explicitly in this case,
\[ \begin{aligned} \mathbf{J} = \left( \begin{array}{cc} \partial \tilde{q} / \partial q & \partial \tilde{q} / \partial p \\ \partial \tilde{p} / \partial q & \partial \tilde{p} / \partial p \end{array} \right) \\ = \left( \begin{array}{cc} 1 + (\partial^2 \mathcal{H} / \partial p \partial q) dt & (\partial^2 \mathcal{H} / \partial p^2) dt \\ - (\partial^2 \mathcal{H} / \partial q^2) dt & 1 - (\partial^2 \mathcal{H} / \partial q \partial p) dt \end{array} \right). \end{aligned} \]
and the determinant is
\[ \begin{aligned} \det J = 1 - (\partial^2 \mathcal{H} / \partial p \partial q)^2 dt^2 + (\partial^2 \mathcal{H} / \partial p^2) (\partial^2 \mathcal{H} / \partial q^2) dt^2 \\ = 1 + (...) dt^2 + ... \end{aligned} \]
The key point here is that there is no linear term in \( dt \), which means that
\[ \begin{aligned} \frac{d (\det J)}{dt} = 0 \Rightarrow \tilde{V} = V. \end{aligned} \]
(This is sort of trivial here, but if we had more than one variable \( q \), then the vanishing of the linear term involves canceling the partial derivatives on the diagonal against each other.) This gives us Liouville's theorem; if we start with a phase-space volume and then evolve it according to some Hamiltonian, the volume of that region will not change, no matter how its shape is distorted.
This is a little reminiscent of Heisenberg's uncertainty principle, in fact; if we start with some distribution of particles with spread \( \Delta q \) and \( \Delta p \) in their positions and momenta, then Liouville's theorem tells us that the product \( \Delta q \Delta p \) is constant as the system evolves. If we try to squeeze the particles together, their momenta will spread apart, and vice-versa. (The uncertainty principle is much deeper, the main difference being that there is no lower bound on the initial product \( \Delta q \Delta p \) in classical mechanics.)
[canon]: images/fig35-canonical-phase.png width=400px [fall-phase]: images/fig35-freefall-phase.png width=400px [damp-phase]: images/fig35-damped-pendulum-phase.png width=400px