Last time (before the tutorial), we continued our study of the equation of orbit, and had a closer look at orbital energy. We have one more quantity left to derive from our equation: orbital speed. As we saw on the tutorial, in some special cases we can use conservation of energy and angular momentum to access the speed, but let's do the general case now.
Orbital speed
For a variety of applications, it's helpful to know the instantaneous speed of the objects in orbit. We can use the equation of orbit directly: we know that
\[ \begin{aligned} v = \sqrt{\dot{r}^2 + r^2 \dot{\phi}^2} \\ = \sqrt{ \left( \frac{dr}{d\phi} \frac{d\phi}{dt} \right)^2 + r^2 \left( \frac{d\phi}{dt} \right)^2} \\ = \dot{\phi} \sqrt{ \frac{c^2 \epsilon^2 \sin^2 \phi}{(1 + \epsilon \cos \phi)^4} + \frac{c^2}{(1+\epsilon \cos \phi)^2}} \\ = \dot{\phi} \sqrt{ \frac{r^4}{c^2} \epsilon^2 \sin^2 \phi + r^2}, \\ \end{aligned} \]
recognizing the orbital equation for \( r \) in the first term. Recalling that \( \dot{\phi} = L_z / (\mu r^2) \), we can plug back in and simplify, taking out common factors of \( r \) and \( c \) as well:
\[ \begin{aligned} = \frac{r^2}{c} \frac{L_z}{\mu r^2} \sqrt{\frac{c^2}{r^2} + \epsilon^2 \sin^2 \phi} \\ = \sqrt{\frac{\gamma}{\mu c}} \sqrt{ \frac{c^2}{r^2} + \epsilon^2 \sin^2 \phi} \\ \approx \sqrt{\frac{GM}{c}} \sqrt{\frac{c^2}{r^2} + \epsilon^2 \sin^2 \phi}. \end{aligned} \]
for gravity, where \( \gamma \approx GM\mu \). Note that for a nearly circular orbit, \( \epsilon \approx 0 \) and \( c \approx r \), and we just have the simple formula
\[ \begin{aligned} v \approx \sqrt{\frac{GM}{r}}, \end{aligned} \]
corresponding to ordinary circular motion. This gives (for example) the orbital speed of the Earth about the Sun, \( v_E \approx 30 \) km/s, to good approximation.
(A word of caution: note that this is the relative speed of the two orbiting objects, since we're using the vector \( \vec{r} = \vec{r_1} - \vec{r_2} \)! In the situation of, say, a comet orbiting the Sun where one mass is much larger and the center of mass is inside the Sun, then it's just the speed of the comet. But for orbiting objects with comparable masses, don't just apply this formula blindly.)
Once again, it's particularly useful to look at \( r_{\rm min} \), where \( \phi = 0 \): there we find
\[ \begin{aligned} v(r_{\rm min}) = \sqrt{\frac{GM}{c}} \sqrt{\frac{c^2}{r_{\rm min}^2} + \epsilon \sin (0)} \\ = \sqrt{\frac{GMc}{r_{\rm min}^2}}. \end{aligned} \]
This gives another, more direct way to estimate the energy of a particular orbit, if we have a small object orbiting a large one (\( m \ll M \)): then we can estimate
\[ \begin{aligned} E \approx \frac{1}{2} m v^2 - \frac{GmM}{r} \\ = \frac{1}{2} m \frac{GMc}{r_{\rm min}^2} - \frac{GmM}{r_{\rm min}} \\ = \frac{GMm}{2r_{\rm min}} \left( \epsilon - 1\right) \\ = -\frac{GMm}{2a}. \end{aligned} \]
You can rederive the equation for angular momentum in the same way, by writing \( Lz = m v{\rm min} r_{\rm min} \). We could write down new formulas for different things in terms of different length scales all day, but if you're going to remember one thing, remember the equation of orbit, and if you're going to remember two, then add the orbital speed; you can derive just about everything else without too much trouble.
Summary of orbital formulas
At this point, it's worth summarizing some of the many formulas we've defined. Taylor doesn't do a great job of this in his end-of-chapter summary in my opinion, so here's my attempt at a more useful alternative.
All of the below are valid for the two-body problem subject to a \( 1/r \) central potential,
\[ \begin{aligned} U(r) = -\frac{\gamma}{r}. \end{aligned} \]
From the masses of the two bodies \( m_1 \) and \( m_2 \), we define the total mass \( M \)
\[ \begin{aligned} M = m_1 + m_2 \end{aligned} \]
and the reduced mass \( \mu \)
\[ \begin{aligned} \mu = \frac{m_1 m_2}{m_1 + m_2}. \end{aligned} \]
For the common situation of gravitational interaction with \( m_1 \ll m_2 \), we have the useful approximations
\[ \begin{aligned} m_1 \approx \mu \\ m_2 \approx M \\ \Rightarrow \gamma \approx GM\mu. \end{aligned} \]
Results below that use \( \approx \) are in this specific approximation.
Equation of orbit:
\[ \begin{aligned} r(\phi) = \frac{c}{1 + \epsilon \cos \phi}. \end{aligned} \]
Orbital speed:
\[ \begin{aligned} v(\phi) = \sqrt{\frac{\gamma}{\mu c}} \sqrt{ \frac{c^2}{r^2} + \epsilon^2 \sin^2 \phi} \\ \approx \sqrt{\frac{GM}{c}} \sqrt{\frac{c^2}{r^2} + \epsilon^2 \sin^2 \phi}. \end{aligned} \]
Orbital energy:
\[ \begin{aligned} E = \frac{\gamma}{2c} (\epsilon^2 - 1) \\ \approx \frac{GM\mu}{2c} (\epsilon^2 - 1) \\ \approx -\frac{GM\mu}{2a}\ \ \ {\textrm{(bound orbits only.)}} \end{aligned} \]
Orbital angular momentum:
\[ \begin{aligned} L_z = \sqrt{\gamma \mu c} \\ \approx \mu \sqrt{GMc} \end{aligned} \]
Orbital period:
\[ \begin{aligned} \tau^2 = \frac{\mu}{\gamma} 4\pi^2 a^3 \\ \approx \frac{4\pi^2}{GM} a^3. \end{aligned} \]
Comparison of orbital energy and angular momentum using the simple scaling relations with \( a \) and \( c \) can be particularly useful when we're interested in orbital transfers, i.e. moving an object from one orbital path to another.
Clicker Question
Three orbits of the same satellite are shown. Orbits 1 and 3 have the same major axis. How is the angular momentum related?
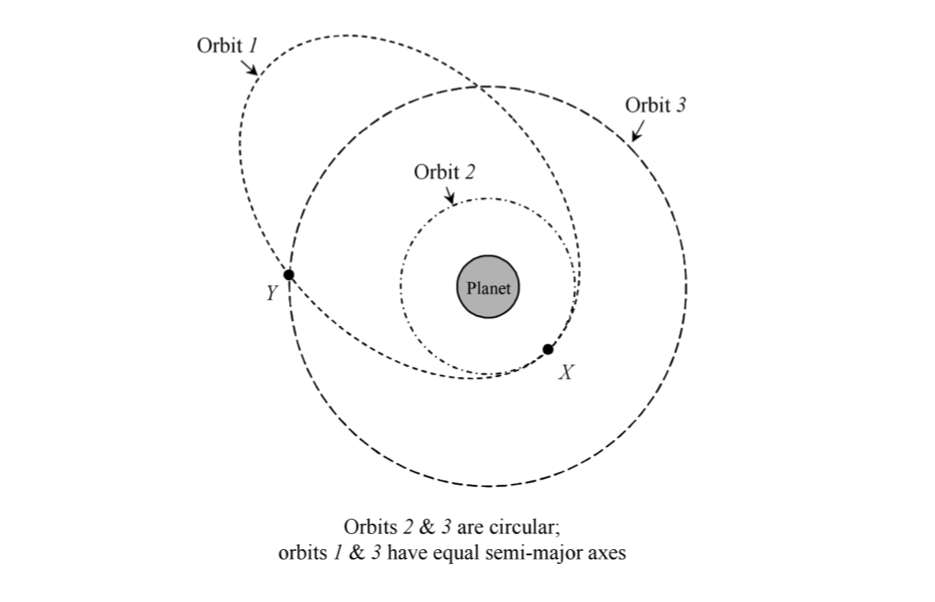
A. \( L_1 > L_2 = L_3 \)
B. \( L_1 < L_2 = L_3 \)
C. \( L_2 < L_1 = L_3 \)
D. \( L_2 < L_1 < L_3 \)
E. \( L_2 > L_1 > L_3 \)
Answer: D
Here we need to use the scaling relationship \( L_z \propto \sqrt{c} \). From the equation of orbit, \( c \) is just the value of the radius at \( \phi = \pi/2 \), i.e. along a line through the planet and perpendicular to the long axis of orbit 1 (roughly in the direction of the "Orbit 3" label - not straight up from the origin!) We can read off the plot that \(c_2 < c_1 < c_3\), which implies that \(L_2 < L_1 < L_3\).
Now that we're done deriving formulas, let's work through a couple more examples that put our orbital model to work.
Example: escape velocity
You've probably solved this problem already last semester, but it's nice to see how it works in our new framework: what is the minimum velocity that an object must have to escape the Earth's gravity?
"Escape" means an unbound orbit by definition, and we know that the least energetic unbound orbital path is the \( E=0 \) orbit, namely a parabolic path with \( \epsilon = 1 \). The point of closest approach \( r_{\textrm{min}} = c/(1+\epsilon) = c/2 \) is the surface of the Earth, so
\[ \begin{aligned} c = 2R_E. \end{aligned} \]
Since the closest approach is at \( \phi = 0 \), using our formula for the speed, we find
\[ \begin{aligned} v_{\textrm{esc}} = \sqrt{\frac{GM_E}{2R_E}} \sqrt{\frac{4R_E^2}{R_E^2} + \sin^2 (0)} \\ = \sqrt{\frac{2GM_E}{R_E}} \end{aligned} \]
or plugging in the numbers \( M_E \approx 6 \times 10^{24} \) kg, \( RE \approx 6.4 \times 10^6 \) m, we find \( v{\textrm{esc}} \approx 11.2 \) km/s.
(By the way, the final speed of the object, plugging in to the formula for \( v \) at \( \phi = \pi \) and \( r \rightarrow \infty \), is zero - as we should expect, since it has zero total energy.)
An interesting discussion came up in class, related to the direction of launch. If we just use standard conservation of energy arguments that don't involve the equation of orbit, then the direction doesn't matter at all (as long as we're not trying to go through solid rock!) But here, I assumed that we start at \( r_{\rm min} \) of the orbit, which means the launch direction must be perpendicular to \( \vec{r} \), i.e. towards the horizon. What is the resolution?
For any orbit, the direction of \( \vec{v} \) is always tangential to the orbit; but for a parabola, this is only perpendicular to \( \vec{r} \) at \( r_{\rm min} \). So changing the launch direction means we must be starting at some other \( \phi \neq 0 \). If we plug in to our orbital formula for a more general \( \phi_0 \), we find (keeping \( \epsilon = 1 \):)
\[ \begin{aligned} v(\phi) = \sqrt{\frac{GM_E}{c}} \sqrt{\frac{c^2}{r(\phi_0)^2} + \sin^2 \phi_0} \\ = \sqrt{\frac{GM_E}{c}} \sqrt{(1 + \cos \phi_0)^2 + \sin^2 \phi_0} \\ = \sqrt{\frac{GM_E}{c}} \sqrt{2(1 + \cos \phi_0)} \\ = \sqrt{\frac{GM_E}{2r(\phi_0)}}, \end{aligned} \]
using the equation of orbit once more at the end. So since \( r(\phi_0) \) is always \( R_E \), changing the launch angle does not change our result for the initial speed - we find the same escape velocity, exactly as conservation of energy predicts! What does change is the scale factor \( c \), and thus the shape of the trajectory that our object will follow as it's escaping.
Example: garbage disposal
Suppose we wanted to launch a rocket filled with nuclear waste off the Earth. Would it cost less energy to send the rocket into the Sun, or to send it completely outside the solar system? (The energy to get into Earth orbit is the same in either case, so we'll work assuming that we start having already escaped Earth's gravity well.)
Let's consider the second case first. As above the escape velocity from radius \( r_E \) (the position of the Earth relative to the Sun) is
\[ \begin{aligned} v_{\textrm{esc},\odot} = \sqrt{\frac{2GM_\odot}{r_E}} = \sqrt{2} v_{E} \end{aligned} \]
where \( v_E = 29.8 \) km/s is the speed of the Earth relative to the Sun.
Since we're launching out of the solar system, it doesn't matter which way we send the waste; the most efficient direction is with the motion of the Earth. The velocity \( u \) relative to the Earth must then be
\[ \begin{aligned} u = (\sqrt{2} - 1) v_{E} \approx 0.41 v_{E} = 12.2\ \mbox{km/s}. \end{aligned} \]
Now, back to the other option: launching into the Sun. Keeping in mind that we want to minimize our total expenditure of energy, what trajectory should we send the rocket on? Since there are multiple possible orbits we may want to consider, we should frame this question in terms of orbital energy. The initial orbital energy \(E_i\) (once the rocket has escaped the Earth, which it will always have to do) is
\[ \begin{aligned} E_i = -\frac{GM_E m}{2r_E} \end{aligned} \]
taking the Earth to be approximately a circular orbit with radius \( a = r_E \). We then want to put our rocket on a new orbit that satisfies two criteria:
- The orbit passes inside the Sun, which implies that \( r_{\rm min} \leq R_{\odot} \), where \( R_{\odot} \) is the Sun's radius;
- The energy difference \(\Delta E = E_f - E_i\) to enter our new orbit is as small as possible.
Clicker Question
In the Sun's frame, which orbital trajectory should we launch the rocket on to get it into the Sun with minimum energy?
A. A straight line
B. A parabolic orbit with \(r_{\rm min} = R_{\odot}\)
C. A parabolic orbit with \(c = R_{\odot}\)
D. An elliptic orbit with \(r_{\rm min} = R_{\odot}, r_{\rm max} = r_E\)
E. An elliptic orbit with \(c = R_{\odot}, r_{\rm max} = r_E\)
Answer: D
Let's deal with the straight line first, since it's the strangest-looking option on the list. In our categorization of orbits, we didn't have any straight lines! This is because we were always assuming some angular momentum \( L_z > 0 \). But if our two-body system has no angular momentum, then clearly the two objects just move directly towards each other, i.e. in a straight line in the radial direction.
This might seem like an intuitively appealing choice, but remember we're not starting from rest in the Sun's frame! Putting our rocket on an \( L_z = 0 \) trajectory therefore means decelerating by the Earth's orbital speed, about 30 km/s. For any of our ordinary \( L_z \neq 0 \) orbits the rocket will have non-zero speed at Earth's radius, so we can do better than the straight line.
For the other four options, we can think purely in terms of orbital energy. Although the parabolic orbits have slightly different shapes, we know that a parabola always has \( E=0 \), which is more energy than an elliptic (bound) orbit will have. In other words, \( \Delta E = (GM_e m)/(2r_E) \) for either parabolic orbit, but any elliptic orbit has \( E < 0 \) and is thus closer in energy to the initial value.
Finally, to compare the two elliptic orbits, we recall that for a bound orbit,
\[ \begin{aligned} E = -\frac{GMm}{2a}. \end{aligned} \]
For option D, we have
\[ \begin{aligned} a_D = (r_{\rm min} + r_{\rm max})/2 = (R_{\odot} + r_E)/2 \approx r_E / 2 \end{aligned} \]
since the radius of the Sun is very small compared to the radius of the Earth's orbit. Thus,
\[ \begin{aligned} E_D = -\frac{GM_e m}{2a_D} \approx -\frac{GM_e m}{r_E} \end{aligned} \]
and we find \( \Delta E \) equal to about half of the initial energy, but further from zero. On the other hand, orbit E has \( r_{\rm min} = c/(1+\epsilon) < R_{\odot} \), so \( a_E \) is smaller, so \( E_E \) is more negative than \( E_D \) and thus \( \Delta E \) is larger. So we conclude that option D will be the least expensive - although the difference between D and E is relatively small compared to differences with the other options.
(By the way, notice that the most efficient orbit actually puts our rocket into the far side of the Sun from the Earth! This is counterintuitive, but the point is that any orbit will have the Sun at a focus, so to intersect the near side of the Sun starting from Earth actually requires extra energy, since you have to fight against gravity, which wants to send the rocket around the Sun.)
Choosing option D, then from the equation of orbit,
\[ \begin{aligned} r(0) = \frac{c}{1+\epsilon} = R_\odot \\ r(\pi) = \frac{c}{1-\epsilon} = r_E. \end{aligned} \]
We can write
\[ \begin{aligned} r_E - R_\odot = \frac{2c\epsilon}{1-\epsilon^2} \\ r_E + R_\odot = \frac{2c}{1-\epsilon^2} \end{aligned} \]
so
\[ \begin{aligned} \epsilon = \frac{r_E - R_\odot}{r_E + R_\odot} \approx 0.991 \end{aligned} \]
and
\[ \begin{aligned} c = r_E (1-\epsilon) = 0.009 r_E. \end{aligned} \]
From above, the speed of the rocket at the Earth must be
\[ \begin{aligned} v = \sqrt{\frac{GM_\odot}{c}} \frac{c}{r_E} = \sqrt{\frac{0.009 GM_\odot}{r_E}} \approx 2.8\ {\rm km/s}. \end{aligned} \]
Unfortunately for us, the Earth is already moving about the Sun, with an orbital velocity of 29.8 km/s. So we have to launch in the opposite direction of the Earth's motion with a speed of about \( u=27.0 \) km/s relative to the Earth! Thus, launching out of the Solar System is (by far!) the more energy-efficient option; sending it into the Sun requires more than twice the speed and thus more than four times as much kinetic energy.
Next time: we wrap up orbital mechanics and move on to accelerating frames.