Now that we've studied the fictitious forces appearing in rotating frames in more detail, let's turn to the most interesting application: the effects of the Earth's rotation.
We should start by setting up our coordinates, of course! The Earth is (roughly) a spherical body, so we'll use spherical coordinate \( (r, \theta, \phi) \); on the surface of the Earth, \( r = R_E \) is taken to be constant. The radius of the Earth is roughly
\[ \begin{aligned} R_E \approx 6400\ \textrm{km}. \end{aligned} \]
The Earth is spinning about an axis, of course, but which way does the angular velocity vector point?
Clicker Question
_Which way does the angular velocity vector of the Earth, \(\Omega_E\), point?_
A. Out of the north pole
B. Out of the south pole
C. Towards the Sun
D. Out of the equator
Answer: A
The Earth rotates to the east (the direction of the sunrise!). This is counter-clockwise when viewed from the north pole down, so the Earth's angular velocity vector \( \vec{\Omega}_E \) points up at the north pole.
Once more, we should note the numeric value of the rotation: it's straightforward to see that
\[ \begin{aligned} \Omega_E = \frac{2\pi}{24\ \rm{h} \times 3600\ \rm{s/h}} = 7.3 \times 10^{-5}\ \rm{rad}/\rm{s}. \end{aligned} \]
Be aware that the standard angular coordinates used to locate positions on the Earth are longitude and latitude, and these are not quite the same as ordinary spherical coordinates! Let's look at a sketch:
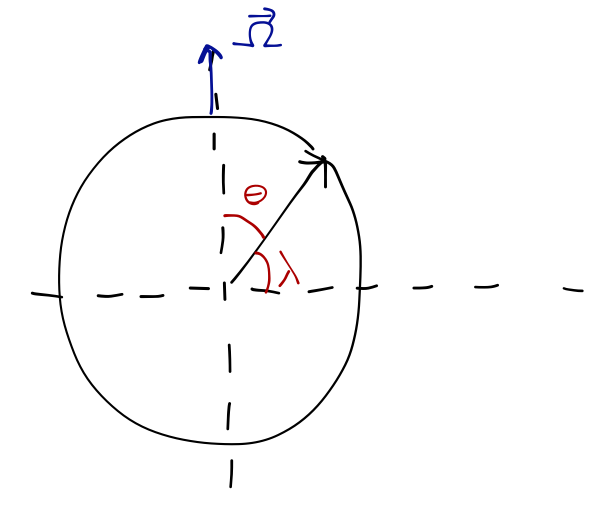
Longitude is exactly the azimuthal spherical angle \( \phi \) which you can't see in this side-on view. The zero of longitude is set at the prime meridian, which is a north-south line passing through Greenwich in the UK. On the other hand, latitude is almost the standard spherical coordinate \( \theta \), but not quite! Latitude \( \lambda \) has its zero at the equator, while our usual \( \theta \) is zero at the pole (specifically, the north pole.)
More confusingly, \( \lambda \) isn't usually labeled as positive or negative, but "north" or "south". So to convert from \( \lambda \) to \( \theta \), we have two formulas:
\[ \begin{aligned} \theta = \pi/2 - \lambda\ \textrm{(north)} \\ \theta = \pi/2 + \lambda\ \textrm{(south)}. \end{aligned} \]
So Boulder is at \( \lambda = 40^\circ N \), which is at \( \theta = 50^\circ \). The more familiar coordinate \( \theta \) is also known as the co-latitude.
Centrifugal force on the Earth
Let's think about the Earth's centrifugal force first. As we saw before, orienting the Earth's angular velocity vector in the \( +\hat{z} \) direction leads to a centrifugal force that points outwards from the axis. In cylindrical coordinates, we have simply:
\[ \begin{aligned} \vec{F}_{\textrm{cf}} = m \Omega_E^2\ \rho \hat{\rho}. \end{aligned} \]
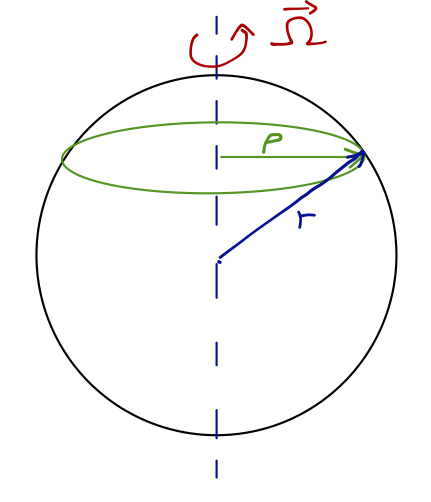
We can immediately see that the effect will be zero at the poles (where \( \rho = 0 \)), and maximum at the equator. (If you step on a scale at the equator, you will actually weigh slightly less than you do at the north or south pole!)
If we want to actually calculate effects at the Earth's surface, we should switch back to spherical coordinates, since cylindrical coordinates aren't very convenient. In spherical coordinates, we can easily look up that the unit vector \( \hat{\rho} \) becomes
\[ \begin{aligned} \hat{\rho} = \sin \theta \hat{r} + \cos \theta \hat{\theta}. \end{aligned} \]
The magnitude of \( \rho \), meanwhile, can be easily determined from our sketch above to be
\[ \begin{aligned} \rho = R_E \sin \theta \end{aligned} \]
so combining, the centrifugal force anywhere on the Earth's surface is:
\[ \begin{aligned} \vec{F}_{\textrm{cf}, E} = m \Omega_E^2 R_E (\sin^2 \theta\ \hat{r} + \sin \theta \cos \theta\ \hat{\theta}). \end{aligned} \]
The radial component is propotional to \( m \), and directly opposite the gravitational force! Thus, if we try to measure \( g \) at different latitudes, our results will be slightly different due to the centrifugal force (and also due to the fact that the Earth isn't perfectly spherical.)
What about the magnitude? We see that on the equator (\( \theta = \pi/2 \)),
\[ \begin{aligned} a_{\textrm{cf}} = \Omega_E^2 R_E \approx 0.034\ \rm{m}/\rm{s}^2 \end{aligned} \]
so you can see that this effect is always small compared to the gravitational acceleration of 9.8 \( {\rm m}/{\rm s}^2 \). (If you weigh 150 pounds, the difference between your weight at the pole and the equator resulting from this effect is about 0.5 pounds.)
Away from the poles and equator, we also have a tangential centrifugal force. This is proportional to mass again, so it looks like a modification of \( F_g \), but now the direction changes too! Explicitly, we can write
\[ \begin{aligned} \vec{g} = \vec{g}_0 + \vec{F}_{\textrm{cf},E}/m = (-g_0 + \Omega_E^2 R_E \sin^2 \theta) \hat{r} + \Omega_E^2 R_E \sin \theta \cos \theta\ \hat{\theta}. \end{aligned} \]
This causes a deflection angle \( \alpha \) between the direction of gravity \( \vec{g}_0 \) and the direction of free-fall acceleration \( \vec{g} \). The deflection is maxized at \( \theta = \pm45^\circ \), where
\[ \begin{aligned} \tan \alpha \approx \alpha = \frac{\Omega_E^2 R_E/2}{g} = \frac{0.017\ \rm{m/s}^2}{9.8\ \rm{m/s}^2} \approx 0.0017\ \rm{rad} \approx 0.1^\circ. \end{aligned} \]
In principle, this is a measurable deflection! In practice, defining "vertical" is extremely difficult; almost any experiment you can think of will give you the direction of \( \vec{g} \) and not \( \vec{g}_0 \). So we generally define "vertical" to include the centrifugal terms, and deal with the difference in the few, very specialized cases where it matters.
Should we worry that now that we've changed the definition of vertical, the \( \hat{\theta} \) component will change our conclusion about how our perceived weight varies over the surface of the Earth? Weight is just given by \( mg \), which we can now work out explicitly:
\[ \begin{aligned} |\vec{g}| = (g_0 - \Omega_E^2 R_E \sin^2 \theta)^2 + \Omega_E^4 R_E^2 \sin^2 \theta \cos^2 \theta \\ = g_0^2 + \Omega_E^4 R_E^2 \sin^4 \theta - 2g_0 \Omega_E^2 R_E \sin^2 \theta + \Omega_E^4 R_E^2 \sin^2 \theta \cos^2 \theta \\ = g_0^2 - \Omega_E^2 R_E \sin^2 \theta (2g_0 - \Omega_E^2 R_E). \end{aligned} \]
We find another correction term which is always negative and proportional to \( \sin^2 \theta \), but since \( \Omega_E^2 R_E \ll g_0 \), this extra effect is even smaller by another factor of 1/300 or so.
The Coriolis force on the Earth
The Coriolis force acts on moving objects according to their velocity \( \vec{v} = \dot{\vec{r}} \) with respect to the rotating frame.
\[ \begin{aligned} \vec{F}_{\textrm{cor}} = 2m \dot{\vec{r}} \times \vec{\Omega} = 2m \vec{v} \times \vec{\Omega}. \end{aligned} \]
The direction of the force depends on the direction of \( \vec{v} \). One helpful observation: if you replace \( 2m \) with \( q \) and \( \vec{\Omega} \) with \( \vec{B} \), this is just the expression for magnetic force, which might help your intuition for how the Coriolis force acts.
On the Earth, the Coriolis force tends to be dwarfed by even the centrifugal force. For an object moving at, say, 40 m/s (an MLB fastball) and perpendicular to \( \Omega \), the acceleration is
\[ \begin{aligned} a_{\textrm{cor},E} = 2v \Omega_E = 2(40\ \rm{m/s}) (7.3\times 10^{-5}\ \rm{s}^{-1}) \approx 0.006\ \rm{m/s}^2. \end{aligned} \]
But the Coriolis effect can become important either for objects moving much faster, or for objects in motion for a long time so that the cumulative effect matters.
What is the direction of the Coriolis force? For motion parallel to the Earth's surface, we can use a top-down picture from above the north pole:
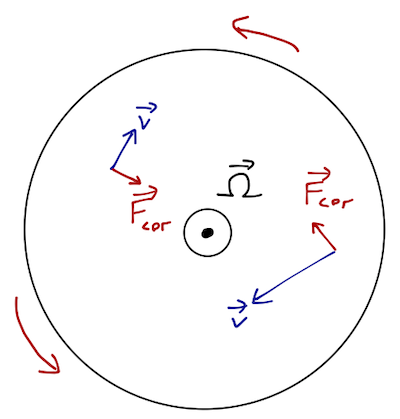
For any direction of \( \vec{v} \), the deflection due to the Coriolis force is to the right on this diagram (which shows the entire northern hemisphere.) If you're not convinced, use the right-hand rule: rotate your hand around to keep \( \vec{\Omega} \) fixed and move \( \vec{v} \).
In the southern hemisphere, the effect reverses; we can draw the same diagram looking down from the south pole, but now \( \Omega \) is into the page. So the Coriolis force deflects motion to the left in the southern hemisphere.
Clicker Question
If I stand on the equator and throw a ball due east, where will it land?
A. In the northern hemisphere
B. In the southern hemisphere
C. On the equator
Answer: C
The direction of the Coriolis force is determined by \( \vec{v} \times \vec{\Omega} \); at the equator, throwing due east is a tangential velocity to the Earth's motion (east is the \( +\hat{\phi} \) direction, in fact), so the cross product always points directly out from the Earth. Thus the deflection is neither right nor left, and the latitude does not change.
Clicker Question
Now standing at \( 45^{\circ} N \) latitude, I drop the ball straight down. Where does it land, relative to the vertical (defined by \( \vec{g} \))?
A. No deflection, but the amount of time to drop changes
B. To the east
C. To the west
D. To the north
E. To the south
Answer: B
Once again, we apply the right-hand rule, but it requires some extra thought this time! Let's draw the velocity vector on the surface of the Earth:
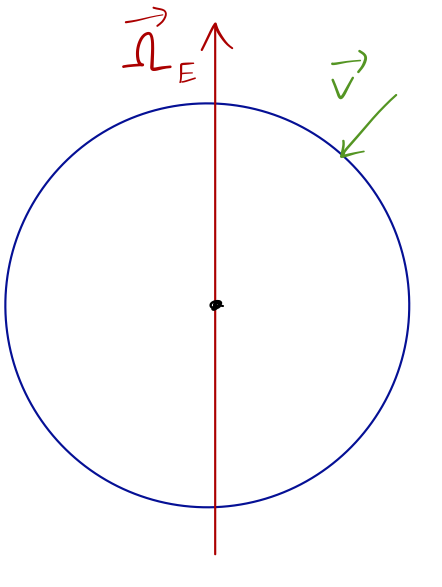
It's always helpful when making these drawings to remember that the fictitious forces don't depend at all on longitude, \( \phi \); this means that we can always rotate our sketch around to simplify it, which I've done here. We see that the component of \( \vec{v} \) that isn't already parallel to \( \vec{\Omega}_E \) is pointing towards the axis of rotation, so that the right-hand rule tells us that \( \vec{v} \times \vec{\Omega}_E \) is directed into the board, in the \( +\hat{\phi} \) direction.
To translate back to cardinal directions, we note that into the board is with the rotation of the Earth, and we remember that the Earth rotates to the east. So the Coriolis force is directed to the east, answer B.
By the way, it should be obvious from our diagram that this answer is correct for any point on the Earth's surface; the acceleration during freefall is always to the east, even in the other hemisphere. You can convince yourself that this is true for any latitude or longitude using the right-hand rule (and remembering that which way "east" is pointing in space depends on what longitude we're sitting at.)
Going beyond just the direction, you can see that the magnitude of the Coriolis effect varies over the surface of the Earth, depending whether the motion is tangential or radial (i.e. throwing an object or dropping it.) For tangential motion, the effect is largest at the poles and zero at the equator for the north/south direction (as we saw), and is constant for east/west motion. For radial motion, the Coriolis force is largest at the equator and zero at the poles.
How about some examples? I mentioned that the Coriolis effect is important for fast motion, or long-lasting motion. The most famous example of fast motion is artillery, specifically naval guns - many battleships would fire shells with muzzle velocities of around 800 m/s, for example. Naval engagements at long range require accurate calculations for the shells to end up where you aim, and the Coriolis force is one of the effects taken into account!
(True story: when British warships were sent to the Falkland Islands in 1982, they noticed that their guns were missing their targets by a substantial amount! Eventually it was noticed that the firing solutions were correcting for the Coriolis effect by including the latitude, but not whether it was north or south latitude, so the force had the wrong sign - the shells were missing by exactly twice the Coriolis deflection.)
Another major application of the Coriolis effect is the explanation of hurricanes and typhoons. These are powerful, rotating storm systems ("tropical cyclones"); they don't form within 500 miles or so of the equator, and they rotate in opposite directions in the two hemispheres. Hurricanes in the northern hemisphere rotate counterclockwise. You might have guessed clockwise, because the Coriolis force is to the right, but we have to be careful!
A hurricane has a defining central eye, which is a low-pressure region: air rushes in towards the eye. As the air rushes in, the Coriolis force deflects it to the right:
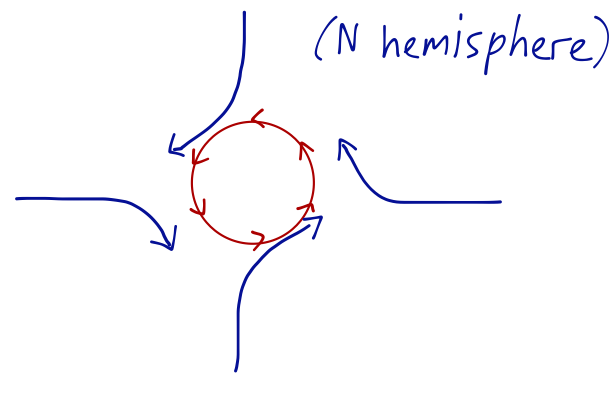
So although an individual air molecule moves clockwise, the net flow of air around the low-pressure region is counter-clockwise, matching the observations. This also explains why cyclones don't form near the equator; the reversal of direction as we cross the equator doesn't support a vortex, instead the net flow of air goes westwards (this gives the "trade winds".)
We can also answer the question, why does a hurricane have an "eye", a calm, cloudless, low-pressure region in the center? Since a hurricane is rotating, it will carry its own set of internal fictitious forces. In particular, the centrifugal force will push air molecules outwards from the center, offsetting the pressure gradient that's pulling them inwards if the air molecules are moving fast enough (and they speed up towards the center, conserving angular momentum: the fastest wind speeds are in the "eye wall" just outside the eye.)
The same argument, in principle, could be applied to water rushing down a sink drain. Here's some experimental homework for you: have a close look at your sink or shower drain next time you use it. Does the water drain clockwise, or counter-clockwise?
Example: Coriolis force and free-fall
Now let's do a more quantiative treatment of how the Coriolis force can deflect free-fall motion. Following Taylor, it's helpful to start by setting up a local Cartesian coordinate system, and writing this equation out in components. Here it is:
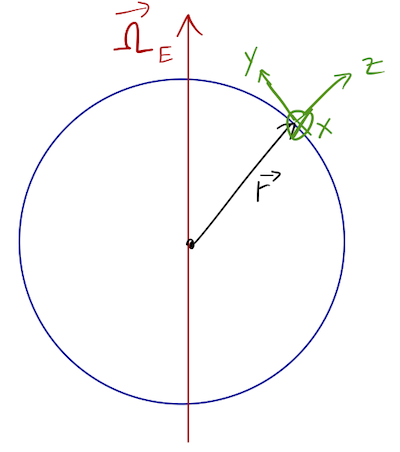
We can think of our three coordinates (x,y,z) as "east", "north", and "up" respectively, which are all correct identifications as long as we don't move too far away. In our local coordinates, we see that the rotation vector \( \vec{\Omega}_E \) has components along \( \hat{y} \) and \( \hat{z} \):
\[ \begin{aligned} \vec{\Omega}_E = (0, \Omega_E \sin \theta, \Omega_E \cos \theta) \end{aligned} \]
so in these coordinates, we see that
\[ \begin{aligned} \dot{\vec{r}} \times \vec{\Omega}_E = \left| \begin{array}{ccc} \hat{x} & \hat{y} & \hat{z} \\ \dot{x} & \dot{y} & \dot{z} \\ 0 & \Omega_E \sin \theta & \Omega_E \cos \theta \end{array} \right| \\ = \Omega_E (\dot{y} \cos \theta - \dot{z} \sin \theta, -\dot{x} \cos \theta, \dot{x} \sin \theta). \end{aligned} \]
Including the gravitational (plus centrifugal) acceleration, our three equations of motion are thus
\[ \begin{aligned} \ddot{x} = 2\Omega_E (\dot{y} \cos \theta - \dot{z} \sin \theta) \\ \ddot{y} = -2\Omega_E \dot{x} \cos \theta \\ \ddot{z} = -g + 2\Omega_E \dot{x} \sin \theta. \end{aligned} \]
These equations do have an analytic solution, but it's somewhat complicated; remembering that \( \Omega_E \) is very small, we can instead carry out a perturbative solution, solving the equations repeatedly with successively more powers of \( \Omega_E \) included.