Your name:

Please read these directions BEFORE beginning.

You may have a normal 8.5 x11 sheet of paper with your own notes.

Please use separate sheets for each numbered problem, and write on one side only. Write your name on the top of each page, and staple your solutions together, thanks.

There are 4 problems (+1 extra credit). All numbered problems are worth 25 pts total..

Feel free to look over my crib sheet before the exam begins.

Don't do integrals if you don't have to! Use symmetry and operator arguments when possible. However, you should always show your work, and explain your reasoning if you feel you can skip algebra by making use of symmetry, etc.

My Crib sheet

1-D time independent Schrodinger eqn:

Time dependent Schrodinger eqn:

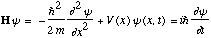
Time dependence of energy eigenfunctions:

Eigenfunctions of momentum:

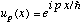
Particle in a 1-D infinite box, 0->L:

Generalized uncertainty principle:

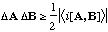
Some operators (and def of commutator)

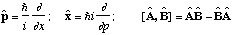
Expectation value:

Hermitian adjoint: , and (AB)⁺ = (B⁺A⁺).

Also, it is always true that

Completeness says the eigenfns |n> of any Hermitian operator, O, satisfy .

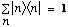Because of this, any vector can be expanded as ,

and 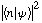is then the probability of measuring the nth eigenvalue of O.

Time evolution:

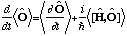
The parity operator 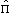is defined by f(x)=f(-x). (It has eigenvalues 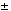1,

with +1 for even functions, and -1 for odd functions)

The energies of a Harmonic oscillator are 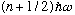, with n=0,1,2,3,...

The eigenfns of the Harmonic oscillator are of the form

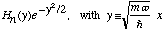
with 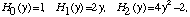etc.

This exam will focus on new material since Exam I, but naturally any material from the earlier parts of this course may be included. Primary new topics we've covered are:

(End of) Ch. 4: Eigenfunctions and Eigenvalues.

Expansion postulate - What is it, how do you use it? Probability interpretation of coefficients.

Parity - How is it defined? What does it tell you? When is it conserved?

Ch. 5: 1-D potentials

E>0: Scattering (from steps, wells, barriers, and delta functions.)

What are the techniques required to find reflection and transmission? What is flux, and what does it have to do with scattering?

Also included in this section is tunnelling.

E<0: Bound states. (Finite well, infinite well, delta and double delta well, and harmonic oscillator. )

What are the techniques required to find the allowed binding energies? What are the qualitative and quantitative aspects of bound state wave functions? (Including properties like orthonormality, parity, number of nodes, time evolution, etc)

Ch. 6 (+ additional material in notes): General structure of Quantum Mechanics

Vectors (and the analogy between vectors and wave functions)

Matrices (and the analogy between matrices and operators)

Dirac notation. Including the connection to "old" wave function notation, and ideas of completeness, projection, expansion, as well as the usual tricks required to manipulate them, including operators and Hermiticity.

Theorems regarding Hermitian operators. (E.g. evalues are real, evectors are orthonormal, etc.)

Postulates of Quantum Mechanics: Involving wavefunctions, eigenvalues, operators and observables, expansion and probabilities.

Simultaneous eigenvectors and compatible observables (and the role of degeneracy)

The generalized uncertainty principle. Including derivation and uses.

The time dependence of operators. Including derivation and uses.