(Issued Wed, Aug 27 Due Wed, Sept 3)

1a) This is meant to be a "quicky", you only need to use Gas. eqns 1-1,

1-12a, and 1-12b. (I just wanted to point out Gas' typo for the value of . Fix it in your book.)

b) Your answer should turn out somewhere between 1000 and 10,000 K's

2a) Do not assume Planck's constant (or equivalently the value of ) to get the work function first, that's cheating!

b) Einstein's explanation of the photoelectric effect hinged on the idea that a single photon causes a single electron to be ejected.

3) It's just conservation of energy and momentum, and most of the work is done for you in my lecture notes, or Gas pp. 12-13. Don't forget you must use relativity here. (The kinetic energy of a particle, in relativity, is defined to be the difference between the total relativistic energy (Gas. 1-18) and the rest mass energy, 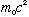, i.e. 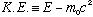) (Can you think of a way to check any part of your answer?)

4) If you can derive Bohr's postulate number 1 (the quantization of angular momentum) then you're done, since we've used the postulates in class to get all the rest... (It's a lovely quantum-y motivation for Bohr's first postulate, which otherwise seems rather mysterious and ad-hoc) Think De Broglie.

5) Use the three postulates (really, just the first one, following through just like we did in class for hydrogen, only here the force law is different)

The constant for the spring is just that, a constant. (You might want to rename it 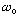to remind yourself)

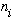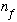When Gas. asks "what is the analog of the Rydberg formula", he means, "what is the formula for the frequency of light emitted when the oscillator drops from an energy level number " " to a level number " ". where the n's are the numbers used in quantizing the angular momentum

The "correspondence principle" says that the frequency of light emitted when you drop from level n to level n-1 is the same as the circular rotational frequency of a particle just sitting in level n (for large n).

(You should discover that the correspondence principle turns out in this case to be satisfied no matter what, even when n is not especially big!)