 or
or
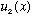 ,
you should be able to write down the formulae by inspection. You may want to
check that you got your normalization right, though.
,
you should be able to write down the formulae by inspection. You may want to
check that you got your normalization right, though.
1) Gas problem 4-3 (problem 3 below) tells you the procedure to find commutators. You don't pick any specific f(x), you must leave it arbitrary.
What do you suppose parity does to the second derivative operator?
2a) No tricks, straightforward.
b) Watch your limits.
c) Think about the sign of your answer. Does it make sense?
d) This useful function is called the theta-step function...
3a) If you worked this out right, the answer turns out proportional to O6.
b) Here, the answer comes out proportional to O1...
4) The particle begins in a well of size 2a. You should be able to write down (and sketch) the starting wave function. (See comments below)
The potential suddenly changes, but wave functions don't (can't) respond instantly. So, at "t=0", the particle is still located in that exact same starting wave function! Only now it's in a bigger box, of size 2b. Gas 4-36 tells you the probability amplitudes to find yourself in any state u_n of the new, big box. Remember, in Eq 4-36, "psi" refers to your starting wave function, and the "u_n"'s refer to the eigenfunctions of the well you are in. Think hard about what the integration limits should be in this problem.
Gas' formulas for square well wavefunctions assume a well that goes from x=0 to x=a. But in this problem, the well goes from x=-a to x=a. So, your wavefunctions aren't quite the same as usual. They're of course
very similar - so similar, that if you just sketch the wave functions
 or
or
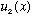 ,
you should be able to write down the formulae by inspection. You may want to
check that you got your normalization right, though.
,
you should be able to write down the formulae by inspection. You may want to
check that you got your normalization right, though.
You will still have one tricky integral to do. You can look it up, use MMA, or just use a trig identity. (See Gas Eq. 4-22 for a clue as to what kind of trig identity you might want to use...)
5) Gas Eq'ns 4-29 through 4-32 contain everything you need for this problem. Your starting wave function can be written as a superposition (sum) of eigenfunctions of the box. Once you've done this, the time dependence is easy, just use Eq. 4-32.
Use Gas' hint right away, it's essential! Remember,
(1-x)^5 = 1 - 5x + 10x^2 - 10x^3 + 5x^4 - x^5.
(You knew that, right? It's from Pascal's triangle... Ask me if you've never seen this.)
For b), look at Eq 4-35.