Issued Wed, Sept 24 Note!: Due Fri, Oct. 3

Exam 1 will be Tu, Sept 30, 7:30 PM

Required reading for this week: Finish Ch. 4. Start Gas. Ch. 5.

There are HINTS for this homework.
1) You are given a particle in a rigid box (width a) with a starting wave function . The un's are the usual, normalized eigenfunctions for the box, with corresponding energy eigenvalues .

a) Find A. (Why is your answer not unique?)

b) What is ?

c) Find 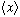(t) (Your answer should have the form 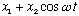. Find )

d) What are the possible results of a single energy measurement? With what probability do they occur? Do these probabilities depend on time?

e) Find 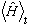, the expectation value of energy as a function of time.

Also find 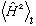, and thus find the uncertainty of energy, .

f) A classical particle in this well would bounce back and forth between the walls. If its energy were equal to the expectation value you found in part d), what would be the frequency of classical motion?

How does this compare with the quantum frequency you found in part c)?

g) Suppose you measure the energy, and then immediately remeasure it. What are now the relative probabilities of the possible outcomes? What is the form of the wavefunction after such a measurement?

2) Gas problem 4-6

3) Gas 4-9

4) Gas 4-10. (Allow A and B to be complex constants)

Like in the quiz, interpret your result for the flux physically. (What does k tell you, physically? What do |A|^2 and |B|^2 represent, physically? What about the signs? What is going on if A=B?)

EXTRA CREDIT:

Gas 4-8