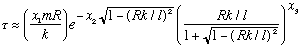1) Gas' hint is good! A and D are arbitrary, meaning YOU can pick them however you like. (0 or nonzero, real or complex, and any equations involving them must still be correct)

A matrix, M, is unitary if the inverse of M is equal to the Hermitian Conjugate of M. The Hermitian Conjugate of M is defined to be the transpose of the complex conjugate of M. (The complex conjugate of a matrix is just where you complex conjugate every single element. The transpose of a matrix is where you flip about the diagonal, i.e. the ij'th element is switched with the ji'th element. The elements on the diagonal, of course "switch" with themselves, and thus stay the same)

2a and b) You don't have to rederive any results that Gasiorowicz has already obtained if you don't want to, for this whole problem! Just use his formulas.

3) Gas 5-4. Ignore Gas' hints!! Just solve the problem directly. Look at Gas eq. 5-63 (the second one, since this is supposed to be the odd solution), and think about what you know already. When you are given the binding energy, think about what this is. (Is it E? -E? V0? E+V0?... Draw a little picture...) I assumed that "range" means the same thing as Gas' parameter "a" for his finite well problems. Your answer for V0 should come out to be some reasonable number of MeV, it turns out to be quite a bit more than 2.2 MeV (i.e, although the well is quite deep, the particle is still just barely bound.) This is a model for a deuteron!

Note: You will need to solve a "nonanalytic" equation - I just used a pocket calculator, and (with the help of some sketches and thought) just had to try out a few values until I closed in on the right answer. Two significant figures is fine for this one...

4) (Gas. 5-11) The integral you get is tricky. Write it as a dimensionless integral before trying to evaluate it! Then look it up. I got something like 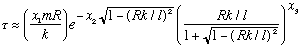(what are x1, 2, and 3?) Check the raw behaviour - as E -> 0, does your lifetime get longer or shorter? (What should it do?)

5) You can solve this problem completely using just the techniques we saw in class for a particle approaching any kind of bump or dip. (E.g, Gas. p 78-79)- write down the most general form of the Schrod Eqn in each region, use continuity arguments, and take advantage of the fact that u(x) must vanish in regions of infinite potential. (Using ideas about flux will also help a lot on this problem)