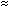 500
keV,
500
keV,
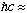 2000
eV Å to keep the numbers simple)
2000
eV Å to keep the numbers simple) Issued Fri, Oct 10 Note! Due Wed, Oct 15
Required reading for this week: Finish Ch. 5 (Note: we won't cover the Kronig-Penney model.)
Start reading Gas Ch. 6
There are HINTS for this homework.
1) An electron is trapped in a well 1 Å wide, and V0=100 eV deep.
(You may use me
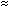 500
keV,
500
keV,
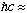 2000
eV Å to keep the numbers simple)
2000
eV Å to keep the numbers simple)
a) How many possible bound states can this electron be in? (Show/explain clearly your reasoning)
b) What is the parity of the eigenstate of maximum energy? How many zeros will this state have? Sketch this eigenstate. (Please indicate clearly on your sketch where the edges of the box are)
c) Suppose your electron is trapped in a single delta function well,
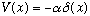 ,
with
,
with
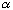 =100
eV Å (i.e., the area under this potential is identical to
the area in parts a and b above). Repeat questions a and b.
=100
eV Å (i.e., the area under this potential is identical to
the area in parts a and b above). Repeat questions a and b.
2) Consider a "double square well" potential, as shown.
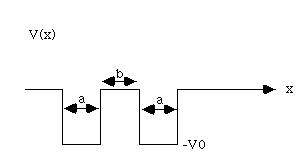
Let V0 and a be fixed,
(and be large enough that
several bound states occur).
This problem is meant to be qualitative, no calculations required!
a) Sketch the ground-state wave function u1(x), and the first excited state u2(x) for the cases i) b=0, ii) b = a and iii) b>>a. (Briefly, discuss your sketches.)
b) Qualitatively, how do the corresponding energies (E1 and E2) vary, as b goes from 0 to infinity? Sketch E1(b) and E2(b) on one graph. (Briefly, discuss your sketch.)
c) The double square well (like the double delta function well from class) is a primitive 1-D model for the potential an electron feels in a diatomic molecule. (The wells represent the electrical attraction of the nuclei) If the nuclei are free to move, they will find the configuration of lowest energy. In view of your conclusions in b) above, does the electron tend to draw the nuclei together, or push them apart? (Never mind the internuclear repulsion, which is something separate!) (Over ->)
3) Find the eigenfunctions, u(x), of the usual Hamiltonian H in the potential

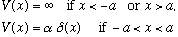
(Don't bother to normalize them). Find the allowed energies (graphical solutions are o.k.) How do the energies compare with the corresponding energies for the well without the delta function in the middle? Sketch the first few eigenfunctions (up to n=3)
4) Consider an electron in a diatomic potential, modeled as a double delta
function,
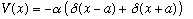 ,
,
with a=1 Angstrom, and alpha = 8 eV A.
a) Find the allowed energies for the (bound) electron, and sketch the wave functions.
b) Find the oscillation frequency,
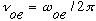 ,
in Hz (as discussed by Gas on p. 98) for such an electron if it is initially in
some superposition of the two allowed energies.
,
in Hz (as discussed by Gas on p. 98) for such an electron if it is initially in
some superposition of the two allowed energies.
What part of the EM spectrum would radiation from these transitions correspond to?
| 3220 main page | Prof. Pollock's page. | Physics Dep't | Send comments |